This Website contains additional material to the SCI²S research papers on "Evolutionary" or "Genetic Fuzzy Systems" and on "Multi-Objective Evolutionary Fuzzy Systems":

F. Herrera, Genetic Fuzzy Systems: Taxonomy, Current Research Trends and Prospects. Evolutionary Intelligence 1 (2008) 27-46, doi: 10.1007/s12065-007-0001-5.

M. Fazzolari, R. Alcalá, Y. Nojima, H. Ishibuchi, F. Herrera., A review of the application of Multi-Objective Evolutionary Systems: Current status and further directions. IEEE Transactions on Fuzzy Systems 21(1) (2013) 45-65, doi: 10.1109/TFUZZ.2012.2201338.

The web is organized according to the following summary:

1. Papers content
2. Introduction to GFSs - What are they?
3. GFSs Taxonomy
4. Pioneer contributions and GFS Milestones (books, special issues, ...)
   1. Pioneer Papers: The birth of GFSs in 1991
   2. GFS Milestones: Books, International Workshops and Special Issues
5. GFS Studies on the ISI Web of Science
   1. GFSs Visibility at the ISI Web of Science: Publications and Citations
   2. High cited papers and GFS Studies on the ISI Web of Science
6. MOEFSs: Introduction, Taxonomy and Further Developments
   1. Introduction
   2. MOEFSs Taxonomy
   3. The Accuracy-Interpretability Trade-Off
   4. Open problems and further developments
7. Slides for GFS Presentations
8. Software and Algorithm Implementations
9. Tackling New Problems with Genetic Fuzzy Systems
10. Recent Journal Papers on Genetic Fuzzy Systems (2007-Present)
11. Related Review Papers and Websites
12. Future Events

Papers content

F. Herrera, Genetic Fuzzy Systems: Taxonomy, Current Research Trends and Prospects. Evolutionary Intelligence 1 (2008) 27-46, doi: 10.1007/s12065-007-0001-5.

Abstract: The use of genetic algorithms for designing fuzzy systems provides them with the learning and adaptation capabilities and is called genetic fuzzy systems (GFSs). This topic has attracted considerable attention in the Computation Intelligence community in the last few years. This paper gives an overview of the field of GFSs, being organized in the following four parts: a) a taxonomy proposal focused on the fuzzy system components involved in the genetic learning process; b) a quick snapshot of the GFSs status paying attention to the pioneer GFSs contributions, showing the GFSs visibility at ISI Web of Science including the most cited papers and pointing out the milestones covered by the books and the special issues in the topic; c) the current research lines together with a discussion on critical considerations of the recent developments; and d) some potential future research directions.

Summary:

1. Introduction.
2. Preliminaries: Fuzzy Rule Based Systems.
3. Taxonomy of Genetic Fuzzy Systems.
   1. Taxonomy.
   2. Genetic Learning: Rule Coding and Cooperation/Competition Evolutionary Process
4. Genetic Fuzzy Systems Outlook.
   1. Pioneer papers: The birth of GFSs in 1991
   2. GFSs visibility at the ISI Web of Science
   3. Some GFS milestones: Books, Special Issues and the Ten Most Cited Papers
   4. The Ten Most Cited Papers at the ISI Web of Science
5. Current Research Trends in GFSs.
   1. Discussing some Current Trends
   2. Some Critical Considerations
6. Genetic Fuzzy Systems: Prospects.
7. Concluding Remarks.

M. Fazzolari, R. Alcalá, Y. Nojima, H. Ishibuchi, F. Herrera. A review of the application of Multi-Objective Evolutionary Systems: Current status and further directions. IEEE Transactions on Fuzzy Systems 21(1) (2013) 45-65, doi: 10.1016/j.eswa.2014.08.002.

Abstract: Over the past few decades, Fuzzy Systems have been widely used in several application fields, thanks to their ability to model complex systems. The design of fuzzy systems has been successfully performed by applying Evolutionary and, in particular, Genetic Algorithms, and recently, this approach has been extended by using Multiobjective Evolutionary Algorithms, which can consider multiple conflicting objectives, instead of a single one. The hybridization between Multiobjective Evolutionary Algorithms and Fuzzy Systems is currently known as Multiobjective Evolutionary Fuzzy Systems. This paper presents an overview of Multiobjective Evolutionary Fuzzy Systems, describing the main contributions on this field and providing a two-level taxonomy of the existing proposals, in order to outline a well-established framework that could help researchers who work on significant further developments. Finally, some considerations of recent trends and potential research directions are presented.

Summary:

1. Introduction
2. Taxonomy Based on the Application of Multiobjective Evolutionary Fuzzy Systems
3. Multiobjective Evolutionary Fuzzy Systems Designed to Generate Fuzzy Rule-Based Systems with Different Accuracy-interpretability Tradeoffs
   1. Approaches to Performing Tuning
   2. Approaches to Performing KB Learning
   3. Approaches That Deal With TSK Fuzzy Rule-Based Systems
   4. Summary of Multiobjective Evolutionary Fuzzy Systems Designed to Generate Fuzzy Rule-Based Systems with Different Accuracy-Interpretability Tradeoffs
4. Multiobjective Evolutionary Fuzzy Systems Designed for Multiobjective Control Problems
   1. Controller Parameters' Identification
   2. Learning of Controller Structure
   3. Summary of Multiobjective Evolutionary Fuzzy Systems Designed for Multiobjective Control Problems
5. Multiobjective Evolutionary Fuzzy Systems Designed for Fuzzy Association Rule Mining
   1. Description of the Existent Contributions
   2. Summary of Multiobjective Evolutionary Fuzzy Systems Designed for Fuzzy Association Rule Mining
6. Open Problems and New Trends in Multiobjective Evolutionary Fuzzy Systems
   1. Performance Evaluation of Multi-Objective Evolutionary Fuzzy Systems Approaches
   2. Reliable Interpretability Measures
   3. Objective Dimensionality
   4. Scalability Issues
   5. Imbalanced Datasets
   6. Automatic Selection of the Most Suitable Solution
   7. Integration of Decision Maker’s Preferences
   8. Design Multiobjective Evolutionary Fuzzy Systems to Generate Type-2 Fuzzy Systems
7. Conclusion

Other two previous reviews:

F. Herrera. Genetic Fuzzy Systems: Status, Critical Considerations and Future Directions. International Journal of Computational Intelligence Research (IJCIR) 1:1 (2005) 59-67.,

O. Cordón, F. Gomide, F. Herrera, F. Hoffmann, L. Magdalena. Ten Years of Genetic Fuzzy Systems: Current Framework and New Trends. Fuzzy Sets and Systems 141:1 (2004) 5-31., doi:10.1016/S0165-0114(03)00111-8..

Introduction to GFSs - What are they?

Computational Intelligence techniques such as artificial neural networks (Rojas R. (1996) Neural networks: A systematic introduction, Springer, Berlin.), fuzzy logic (Yager RR, Filev DP. (1994) Essentials of Fuzzy Modeling and Control, John Wiley & Sons.), and genetic algorithms (GAs) (Holland JH. (197) Adaptation in natural and artificial systems, Ann Arbor: University of Michigan Press.; Goldberg DE. (1989) Genetic algorithms in search, optimization, and machine learning, Addison-Wesley. ) are popular research subjects, since they can deal with complex engineering problems which are difficult to solve by classical methods (Konar A. (2005) Computational Intelligence: Principles, techniques and applications, Springer-Verlag, Berlin).

Hybrid approaches have attracted considerable attention in the Computational Intelligence community. One of the most popular approaches is the hybridization between fuzzy logic and GAs leading to genetic fuzzy systems (GFSs) ( Cordón O, Herrera F, Hoffmann F, Magdalena L (2001) Genetic fuzzy systems. Evolutionary tuning and learning of fuzzy knowledge bases, World Scientific, Singapore). A GFS is basically a fuzzy system augmented by a learning process based on evolutionary computation, which includes genetic algorithms, genetic programming, and evolutionary strategies, among other evolutionary algorithms (EAs) (Eiben AE, Smith JE. (2003). Introduction to evolutionary computation, Springer Verlag, Berlin).

Fuzzy systems are one of the most important areas for the application of the Fuzzy Set Theory. Usually it is considered a model structure in the form of fuzzy rule based systems (FRBSs). FRBSs constitute an extension to classical rule-based systems, because they deal with "IF-THEN" rules, whose antecedents and consequents are composed of fuzzy logic statements, instead of classical ones. They have demonstrated their ability for control problems (Palm R, Driankov D, Hellendoorn. (1997) Model based fuzzy control, Springer-Verlag, Berlin), modelling (Pedrycz W (Ed.). (1996) Fuzzy modelling: Paradigms and practice, Kluwer Academic Press), classification or data mining (Kuncheva L. (2000) Fuzzy classifier design, Springer, Berlin and Ishibuchi H, Nakashima T, Nii M. (2004) Classification and modeling with linguistic information granules: Advanced approaches to linguistic data mining, Springer, Berlin) in a huge number of applications.

The automatic definition of an FRBS can be seen as an optimization or search problem, and GAs are a well known and widely used global search technique with the ability to explore a large search space for suitable solutions only requiring a performance measure. In addition to their ability to find near optimal solutions in complex search spaces, the generic code structure and independent performance features of GAs make them suitable candidates to incorporate a priori knowledge. In the case of FRBSs, this a priori knowledge may be in the form of linguistic variables, fuzzy membership function parameters, fuzzy rules, number of rules, etc. These capabilities extended the use of GAs in the development of a wide range of approaches for designing FRBSs over the last few years. Figure 1 illustrates this idea, where the genetic process learns or tunes different components of an FRBS.

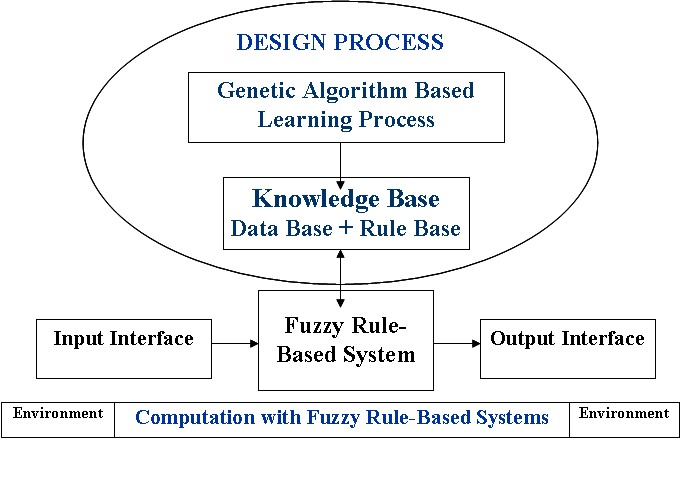
Fig. 1. Genetic fuzzy systems

In the last few years we observe the increase of published papers in the topic due to the high potential of GFSs. Contrary to neural networks, clustering, rule induction and many other machine learning approaches, GAs provide a means to encode and evolve rule antecedent aggregation operators, different rule semantics, rule base aggregation operators and defuzzification methods. Therefore, GAs remain today as one of the fewest knowledge acquisition schemes available to design and, in some sense, optimize FRBSs with respect to the design decisions, allowing decision makers to decide what components are fixed and which ones evolve according to the performance measures.

The predominant type of GFS is that focused on FRBSs. However other kinds of GFSs have been developed, with successful results. They include genetic fuzzy neural networks and genetic fuzzy clustering algorithms. We will not analyze them in this papers. Readers can find an extended introduction to them in (Cordón O, Herrera F, Hoffmann F, Magdalena L. (2001) Genetic fuzzy systems. Evolutionary tuning and learning of fuzzy knowledge bases, World Scientific, Singapore (chapter 10)).

GFSs Taxonomy

The central aspect on the use of GAs for automatic learning of FRBSs is that the design process can be analyzed as a search problem in the space of models, such as the space of rule sets, by means of the coding of the model in a chromosome.

From the optimization point of view, to find an appropriate fuzzy model is equivalent to code it as a parameter structure and then to find the parameter values that give us the optimum for a concrete fitness function. Therefore, the first step in designing a GFS is to decide which parts of the fuzzy system are subjected to optimization by the GA coding them into chromosomes.

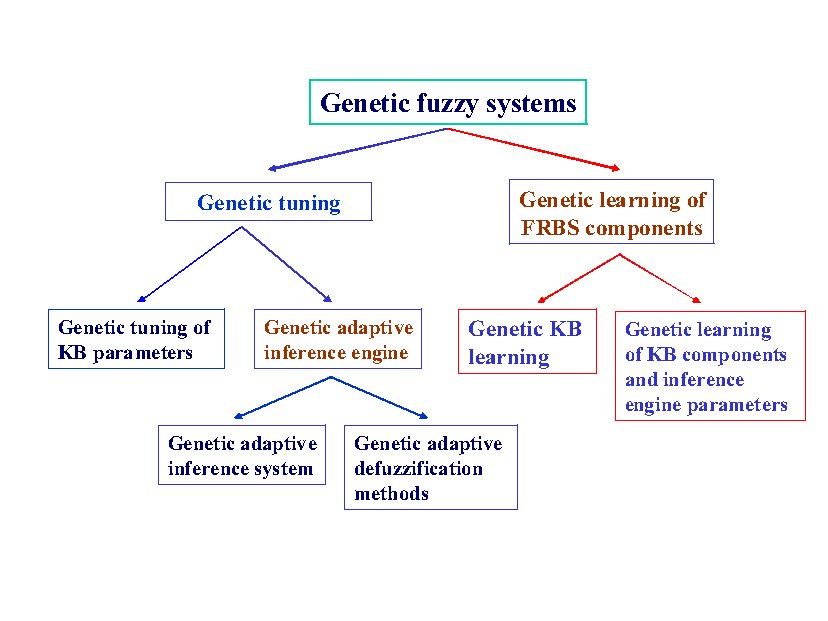
We divide the GFS approaches into two processes, tuning and learning. It is difficult to make a clear distinction between tuning and learning processes, since establishing a precise borderline becomes as difficult as defining the concept of learning itself. The first fact that we have to take into consideration is the existence or not of a previous Knowledge Base (KB), including Data Base (DB) and Rule Base (RB). In the framework of GFSs we can shortly introduce the following distinction.

• Genetic tuning. If there exists a KB, we apply a genetic tuning process for improving the FRBS performance but without changing the existing RB. That is, to adjust FRBS parameters for improving its performance, maintaining the same RB.
• Genetic learning. The second possibility is to learn KB components (where we can even include an adaptive inference engine). That is, to involve the learning of KB components among other FRBS components.

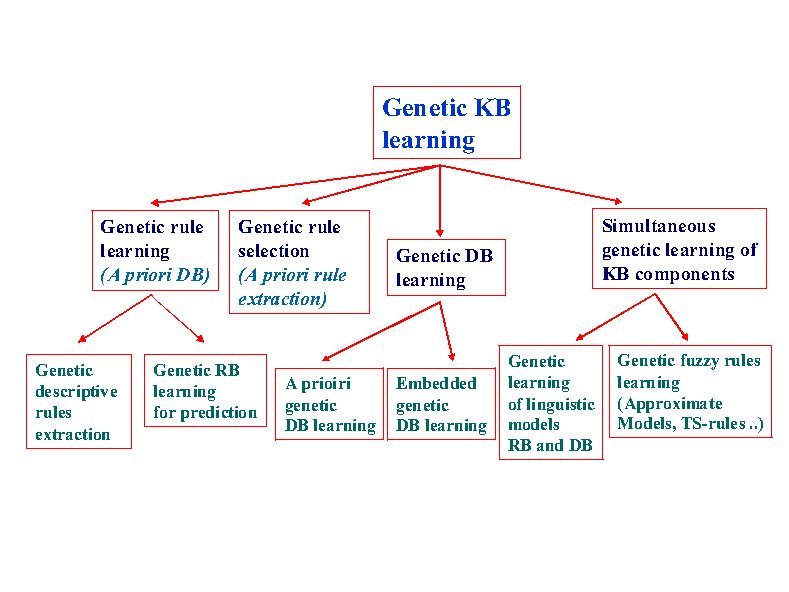
We classify the proposals according to these two processes and according to the FRBS components involved in the genetic learning process. In this way, I propose the taxonomy shown in Figure 4.

Fig. 4. GFSs Taxonomy

There are three main areas in the taxonomy that we can observe in the first tree: genetic tuning, genetic KB learning, and genetic learning of KB components and inference engine parameters. In the following, we shortly analyze the three areas. We will provide some references as examples for every approach, but we do not present an exhaustive list of papers for every approach, this is far from the paper's objective.

Genetic tuning.

With the aim of making the FRBS perform better, some approaches try to improve the preliminary DB definition or the inference engine parameters once the RB has been derived. A graphical representation of this kind of tuning is shown in Figure 5.

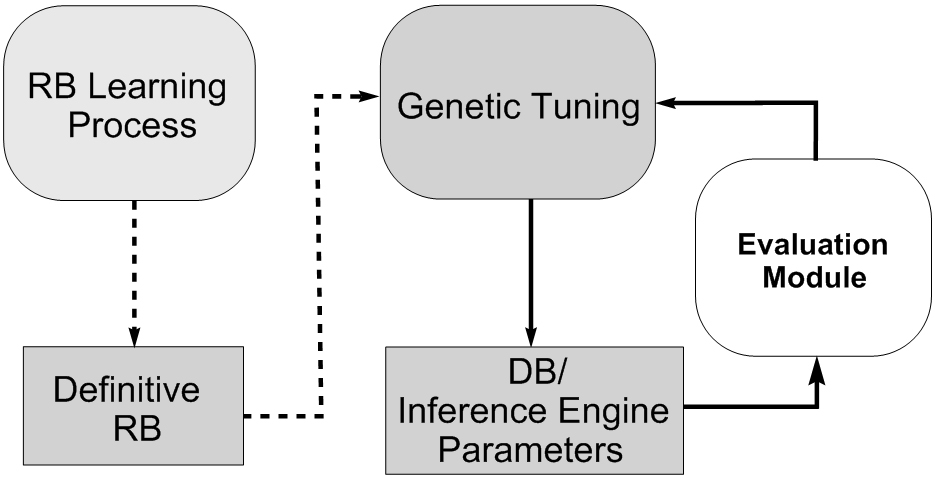
Fig. 5. Genetic tuning process

The following three tuning possibilities can be considered (see the sub-tree under "genetic tuning).

1. Genetic tuning of KB parameters. In order to do so, a tuning process considering the whole KB obtained (the preliminary DB and the derived) is used a posteriori to adjust the membership function parameters. Nevertheless, the tuning process only adjusts the shapes of the membership functions and not the number of linguistic terms in each fuzzy partition, which remains fixed from the beginning of the design process. In (Karr C. (1991) Genetic algorithms for fuzzy controllers, AI Expert 6(2):26-3) we can find a first and classic proposal on tuning. We can also find recent proposals that introduce linguistic modifiers for tuning the membership functions, see (Casillas J, Cordón O, del Jesus MJ, Herrera F. (2005) Genetic tuning of fuzzy rule deep structures preserving interpretability for linguistic modeling, IEEE Trans. on Fuzzy Systems 13(1):13-29, doi: 10.1109/TFUZZ.2004.839670). New rule representation models have also been proposed to perform Lateral Tuning or Lateral and Amplitude Tuning of the membership functions in large search spaces, see (Alcalá R, Alcalá-Fdez J, Herrera F. (2007) A proposal for the genetic lateral tuning of linguistic fuzzy systems and its interaction with rule selection, IEEE Transactions on Fuzzy Systems 15(4):616-635, doi:10.1109/TFUZZ.2006.889880 and Alcalá R, Alcalá-Fdez J, Gacto MJ, Herrera F (2007) Rule base reduction and genetic tuning of fuzzy systems based on the linguistic 3-tuples representation. Soft Computing 11(5):401-419, doi:10.1007/s00500-006-0106-2). Furthermore, specific Multi Objective Evolutionary Algorithms have been recently designed to improve the Tuning performance in (Gacto MJ, Alcalá R, Herrera F (2008) Adaptation and application of multi-objective evolutionary algorithms for rule reduction and parameter tuning of fuzzy rule-based systems. Soft Computing 13:5 (2009) 419-436, doi:10.1007/s00500-008-0359-z)
2. Genetic adaptive inference systems. The main aim of this approach is the use of parameterized expressions in the Inference System, sometimes called Adaptive Inference Systems, for getting higher cooperation among the fuzzy rules and therefore more accurate fuzzy models without loosing the linguistic rule interpretability. In the following references we can find proposals in this area focused in regression and classification: Alcalá-Fdez J, Herrera F, Marquez F, Peregrin A. (2007) Increasing fuzzy rules cooperation based on evolutionary adaptive inference systems, International Journal of Intelligent Systems 22(9):1035-1064, doi:10.1002/int.20237, (2006) Genetic tuning of fuzzy inference within fuzzy classifier systems, Expert Systems with Applications 23:63-82, doi: 10.1111/j.1468-0394.2006.00325.x and Crockett K, Bandar Z, Mclean D. (2007) On the optimization of T-norm parameters within fuzzy decision trees, IEEE International Conference on Fuzzy Systems (FUZZ-IEEE'07), London, UK, pp 103-108
3. Genetic adaptive defuzzification methods. The most used technique in practice, due to its good performance, efficiency and easier implementation, is to apply the defuzzification function to every inferred rule fuzzy set (getting a characteristic value) and to compute them by a weighted average operator. This way to work introduces the possibility of using parameter based average functions, and the use of GAs can allow us to adapt the defuzzification methods. In (Kim D, Choi Y, Lee S. (2002) An accurate COG defuzzifier design using Lamarckian co-adaptation of learning and evolution, Fuzzy Sets Syst. 130(2):207-225, doi: 10.1016/S0165-0114(01)00167-1) we can find a proposal in this area.

 

Genetic KB learning.

As a second big area we find the learning of KB components. Following, we describe the four approaches that can be found within the genetic learning of a KB (see the second tree under "genetic KB learning").

• Genetic rule learning. Most of the approaches proposed to automatically learn the KB from numerical information have focused on the RB learning, using a predefined DB. The usual way to define this DB involves choosing a number of linguistic terms for each linguistic variable (an odd number between 3 and 9, which is usually the same for all the variables) and setting the values of the system parameters by an uniform distribution of the linguistic terms into the variable universe of discourse. Figure 6 shows graphically this type of RB learning. The pioneer proposal for this approach can be found in (Thrift P. (1991) Fuzzy logic synthesis with genetic algorithms, In: Proc. of 4th International Conference on Genetic Algorithms (ICGA'91), pp 509-513).
•  

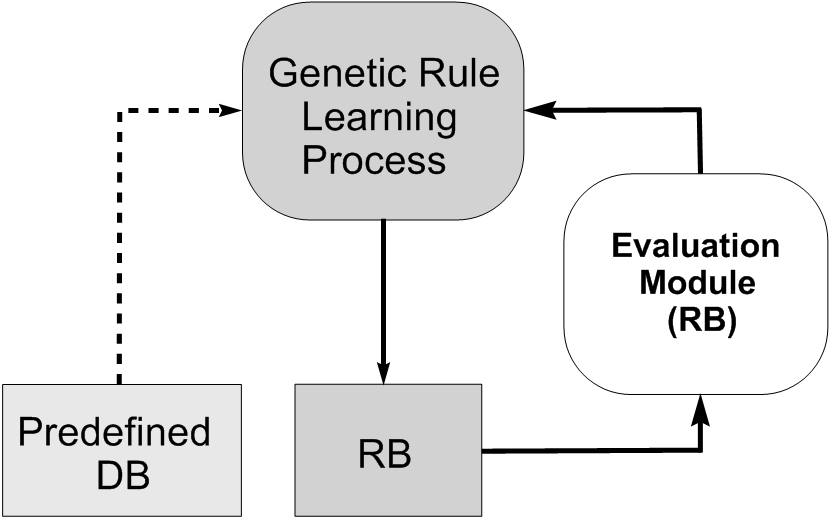
Fig. 6. Genetic rule learning process

On the other hand, we also find approaches that are focused on the extraction of some descriptive rules for data mining problems (association rules, subgroup discovery, ...) (Kaya M, Alhajj R. (2005) Genetic algorithm based framework for mining fuzzy association rules, Fuzzy Sets and Systems 152(3): 587-601, doi: 10.1016/j.fss.2004.09.014 and del del Jesus MJ, González P, Herrera F, Mesonero M. (2007) Evolutionary fuzzy rule induction process for subgroup discovery: A case study in marketing, IEEE Transactions on Fuzzy Systems 15(4):578-592, doi:10.1109/TFUZZ.2006.890662)

• Genetic rule selection. Sometimes we have a big number of rules extracted via a data mining method that only provide us a big number of rules associated to our problem. A big RB and an excessive number of rules makes difficult to understand the FRBS behaviour. Thus we can find different kinds of rules in a fuzzy rule set: irrelevant rules, redundant rules, erroneous rules and conflictive rules, which perturb the FRBS performance when they coexist with others. To face this problem we can use a genetic rule selection process for obtaining an optimized subset of rules from a previous fuzzy rule set by selecting some of them. Figure 7 graphically shows this idea. In (Ishibuchi H, Nozaki K, Yamamoto N, Tanaka H. (1995) Selection fuzzy IF-THEN rules for classification problems using genetic algorithms, IEEE Transactions on Fuzzy Systems 3(3): 260-270, doi: 10.1109/91.413232) we can find the most classic and first contribution in this area and in (Ishibuchi H, Murata T, Turksen IB. (1997) Single-objective and two-objective genetic algorithms for selecting linguistic rules for pattern classification problems, Fuzzy Sets and Systems 8(2):135-150, doi: 10.1016/S0165-0114(96)00098-X) we can find the first journal paper on multiobjective genetic rule selection.

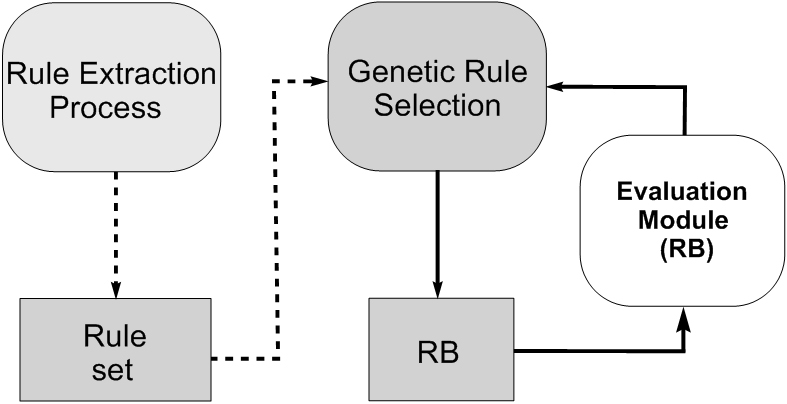
Fig. 7. Genetic rule selection process

We must point out that rule selection can be combined with tuning approaches, trying to get a good rule set together with a tuned set of parameters. In (Casillas J, Cordón O, del Jesus MJ, Herrera F. (2005) Genetic tuning of fuzzy rule deep structures preserving interpretability for linguistic modeling, IEEE Trans. on Fuzzy Systems 13(1):13-29, doi: 10.1109/TFUZZ.2004.839670 and Alcalá R, Alcalá-Fdez J, Herrera F. (2007) A proposal for the genetic lateral tuning of linguistic fuzzy systems and its interaction with rule selection, IEEE Transactions on Fuzzy Systems 15(4):616-635, doi:10.1109/TFUZZ.2006.889880) we can find two recent proposal that combines genetic tuning with rule selection. Figure 8 presents the scheme of the hybrid model proposed in the latter reference. In (Alcalá R, Gacto MJ, Herrera F, Alcalá-Fdez J. (2007) A multi-objective genetic algorithm for tuning and rule selection to obtain accurate and compact linguistic fuzzy rule-based systems, International Journal of Uncertainty Fuzziness and Knowledge-Based Systems 15(5):539-557, doi:10.1142/S0218488507004868) a specific Multi Objective Evolutionary Algorithms has been also proposed to obtain compact but still accurate linguistic models.

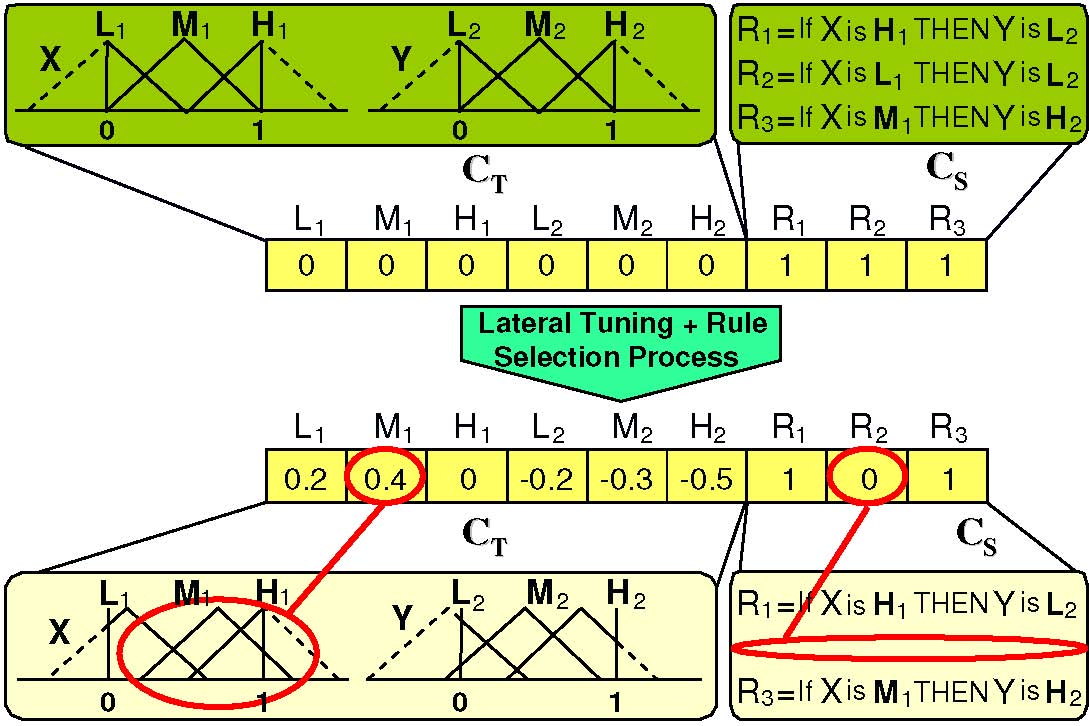
Fig. 8. Example of genetic lateral tuning and rule selection

• Genetic DB learning. There is another way to generate the whole KB that considers two different processes to derive both components, DB and RB. A DB generation process allows us to learn the shape or the membership functions and other DB components such as the scaling functions, the granularity of the fuzzy partitions, ... This DB generation process can use a measure for evaluating the quality of the DB, we can call them as "A priori genetic DB learning". The second possibility is to consider and embedded genetic learning process where the DB generation process wraps an RB learning one working as follows: each time a DB has been obtained by the DB definition process, the RB generation method is used to derive the rules, and some type of error measure is used to validate the whole KB obtained. We should note this operation mode involves a partitioning of the KB learning problem. These two kinds of learning models are represented in Figure 9. In (Cordón O, Herrera F, Villar P. (2001) Generating the knowledge base of a fuzzy rule-based system by the genetic learning of data base, IEEE Transactions on Fuzzy Systems 9(4):667-674, doi: 10.1109/91.940977) we can find a proposal following the embedded genetic DB learning.

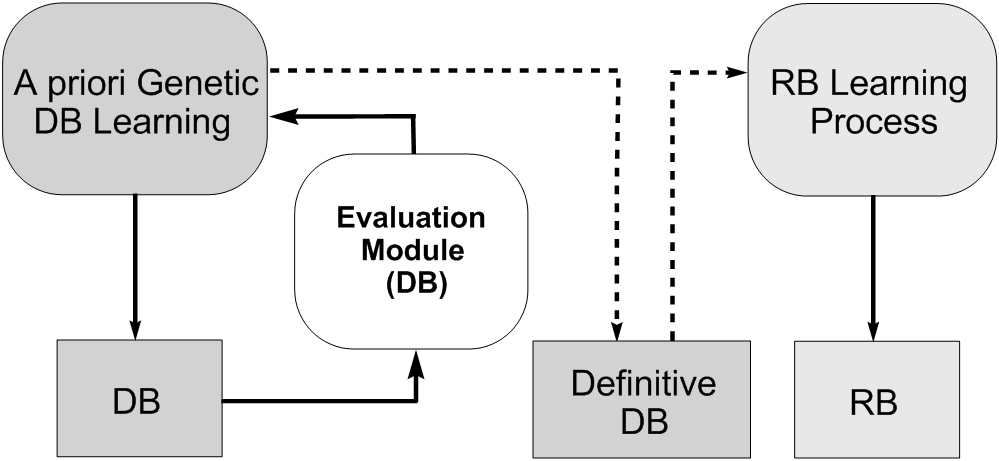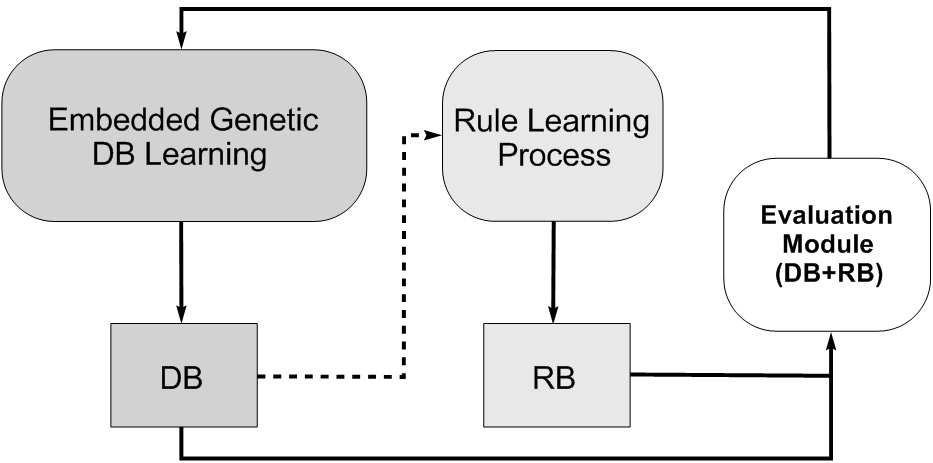Fig. 9. Genetic DB learning (a priori and embedded)

• Simultaneous genetic learning of KB components. Other approaches try to learn the two components of the KB simultaneously. This kind of learning is depicted in Figure 10. Working in this way, they have the possibility of generating better definitions but there is a need to deal with a larger search space that makes the learning process more difficult and slow. In (Homaifar A, Mccormick E. (1995) Simultaneous design of membership functions and rule sets for fuzzy controllers using genetic algorithms, IEEE Transactions on Fuzzy Systems 3(2):129-139, doi: 10.1109/91.388168) we can find a contribution that is a reference in the simultaneous genetic KB learning process.

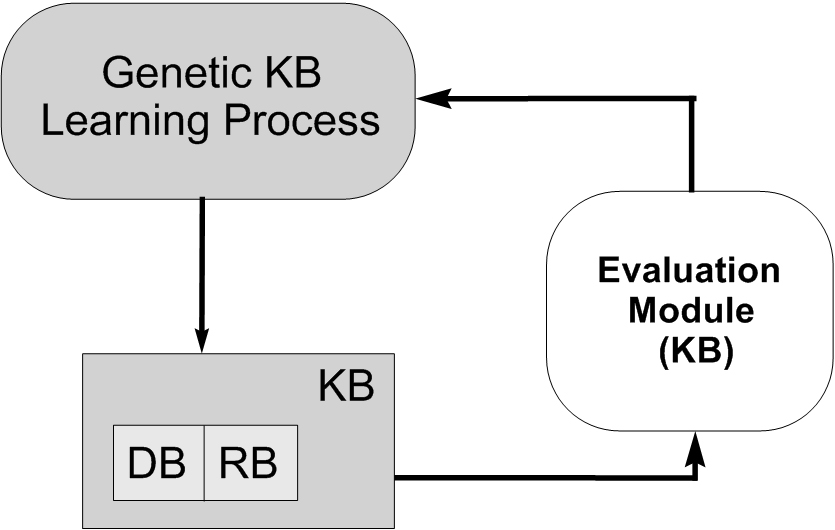
Fig. 10. Genetic KB learning process

 

Genetic learning of KB components and inference engine parameters.

This is the last area of GFSs taxonomy, belonging to a hybrid model between adaptive inference engine and KB components learning. We can find novel approaches that try to find high cooperation between the inference engine via parameters adaptation and the learning of KB components, including both in a simultaneous learning process. In (Márquez FA, Peregrín A, Herrera F. (2007) Cooperative evolutionary learning of linguistic fuzzy rules and parametric aggregation connectors for Mamdani fuzzy systems, IEEE Transactions on Fuzzy Systems 15(6): 1162-1178, doi: 10.1109/TFUZZ.2007.904121) we can find a recent proposal to learn a linguistic RB and the parametric aggregation connectors of the inference and defuzzification in a single step. Figure 11 presents the coding scheme of the model proposed in this paper.

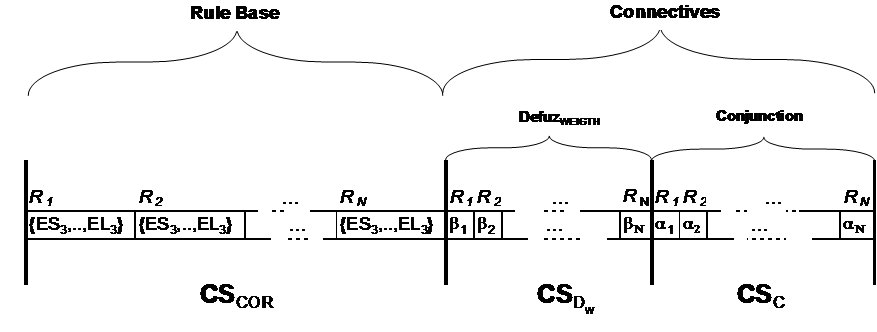
Fig. 11. Example of the coding scheme for learning an RB and the inference connective parameters

Pioneer contributions and GFS Milestones

This section tries to present a quick snapshot of the GFS status stressing the following points:

• Pioneer Papers: The birth of GFSs in 1991.
• Some GFS Milestones: Books, International Workshops and Special Issues.

Pioneer Papers: The birth of GFSs in 1991.

Following, are shortly described the four pioneer papers, that introduced the first genetic tuning and genetic RB learning proposals following the Michigan and the Pittsburgh approaches.

Karr's AI Expert paper (Genetic tuning of the DB)

Karr C. Genetic algorithms for fuzzy controller. AI Expert 6(2):26-33,

The pioneer work in genetic tuning considers linguistic FRBSs. The DB definition is encoded in the chromosome, which contains the concatenated parameters of the input and output fuzzy sets.

Valenzuela-Rendon's ICGA91 paper (Linguistic RB Learning, Michigan approach)

Valenzuela-Rendon M. (1991) The fuzzy classifier system: A classifier system for continuously varying variables. In: Proc. of 4th International Conference on Genetic Algorithms (ICGA'91), pp 346-353,

This proposal presents the first GFS based on the Michigan approach for learning RBs with DNF fuzzy rules. It employs a reward distribution scheme that requires knowledge of the correct action, and thus, must be considered as a supervised learning algorithm. The author later extended the original proposal, in order to enable true reinforcement learning (Valenzuela-Rendon M. (1998) Reinforcement learning in the fuzzy classifier system. Expert Systems with Applications 14:237-247, pp 346-353, doi: 10.1016/S0957-4174(97)00077-8).

Thrift's ICGA91 paper (Linguistic RB Learning, Pittsburgh approach)

Thrift P. (1991) Fuzzy logic synthesis with genetic algorithms. In: Proc. of 4th International Conference on Genetic Algorithms (ICGA'91), pp 509-513,

This is the pioneer work on the Pittsburgh approach for learning RBs. This method works by using a complete decision table that represents a special case of crisp relation defined over the collections of fuzzy sets corresponding to the input and output variables. A chromosome is obtained from the decision table by going row-wise and coding each output fuzzy set as an integer including a "null" label as a 0. Therefore, the GA employs an integer coding.

Pham and Karaboga's Journal of Systems Engineering paper (Relational matrix-based FRBS learning)

Pham DT, Karaboga D. (1991) Optimum design of fuzzy logic controllers using genetic algorithms. Journal of Systems Engineering 1:114-118. ,

This is a quite different approach that uses a fuzzy relation R instead of the classical crisp relation (decision table). The GA is used to modify the fuzzy relational matrix of an one-input, one-output fuzzy model. The chromosome is obtained by concatenating the M·N elements of R, where M and N are the number of linguistic terms associated with the input and output variables. The elements of R are real numbers in the interval [0,1].

After the publication of these four pioneer proposals we can find an increasing number of contributions in the specialized literature with proposals that cover all the different areas of the taxonomy, with a rich body of literature on this topic and with high visibility. This is shown in the next section, where we shortly present the visibility of GFSs at the ISI Web of Science.

Some GFS Milestones: Books, International Workshops and Special Issues.

For beginners, we present next the GFS milestones associated to the books, international workshops and special issues published in the specialized literature.

1) Books. We can find two authored books and three edited ones:

• A. Geyer-Schulz. Fuzzy Rule-Based Expert Systems and Genetic Machine Learning. Physica-Verlag, 1995.

This is the first GFS book. It is a very specific book focused on fuzzy classifier systems (Michigan approach) and RB learning with genetic programming.

• O. Cordón, F. Herrera, F. Hoffmann and L. Magdalena. Genetic Fuzzy Systems. Evolutionary Tuning and Learning of Fuzzy Knowledge Bases, World Scientific, 2001.

This is the first general GFS book. It covers the overall state of the art of GFSs by that time. These three following books compile an important number of contributions that gave maturity to the topic.

• F. Herrera and J.L. Verdegay (Eds.). Genetic Algorithms and Soft Computing. Physica-Verlag, 1996.
• E. Sanchez, Shibata and L. Zadeh (Eds.). Genetic Algorithms and Fuzzy Logic Systems. Soft Computing Perspectives. World Scientific, 1997.
• W. Pedrycz (Ed.). Fuzzy Evolutionary Computation. Kluwer Academic Publishers, 1997.

2) International Workshops. We enumerate here some of the international workshops that supports GFSs:

6th IEEE International Workshop on Genetic and Evolutionary Fuzzy Systems (GEFS13). Singapore, 16-19 April 2013. , Conference Co-chairs: R. Alcalá and Y. Nojima. Publicity Co-chairs: J. Alcalá-Fdez, P. Ducange and M.J. Gacto. Web Page of the Workshop

5th IEEE International Workshop on Genetic and Evolutionary Fuzzy Systems (GEFS11). Paris (France), 11-15 April 2011. , Conference Co-chairs: R. Alcalá and Y. Nojima. Publicity Co-chairs: J. Alcalá-Fdez and P. Ducange. Web Page of the Workshop

Fourth International Workshop on Genetic and Evolutionary Fuzzy Systems (GEFS10). Mieres (Asturias, Spain), 17-19 March 2010. , Conference Co-chairs: O. Cordón and L. Magdalena. Program Co-chairs: R. Alcalá and Y. Nojima. Web Page of the Workshop

3rd International Workshop on Genetic and Evolving Fuzzy Systems (GEFS08). Witten-Bommerholz (Germany), 4-7 March 2008. , Program Chair: O. Cordón. Web Page of the Workshop

International Symposium on Evolving Fuzzy Systems (EFS06). IEEE. Ambleside (UK), September 2006. , International Program Committee Chair: O. Cordón.

First International Workshop on Genetic Fuzzy Systems (GFS05). Granada (Spain), March 17-19, 2005. , Conference Co-chairs: F. Herrera, O. Cordón Organizing Committee: J. Alcalá-Fdez, R. Alcalá, J. Casillas, P. Villar. Web Page of the Workshop

3) Journal Special Issues. Next, we provide a list of the journal special issues devoted to GFSs, including important contributions to all topics of GFSs. We include a global table of contents for these special issues.

• F. Herrera. Special Issue on Genetic Fuzzy Systems for Control and Robotics. International Journal of Approximate Reasoning, Volume 17, Number 4, November 1997. Table of contents
• F. Herrera and L. Magdalena. Special Issue on Genetic Fuzzy Systems. International Journal of Intelligent Systems, Volume 13, Numbers 10-11, Oct.-Nov. 1998. Table of contents
• O. Cordón, F. Herrera, F. Hoffmann and L. Magdalena. Special Issue on Recent Advances in Genetic Fuzzy Systems. Information Sciences, Volume 136, Numbers 1-4 , August 2001. Table of contents
• O. Cordón, F. Gomide, F. Herrera, F. Hoffmann, L. Magdalena. Special Issue on Genetic Fuzzy Systems. Fuzzy Sets and Systems, Volume 141, Number 1, January 2004. Table of contents
• J. Casillas, M.J. del Jesus, F. Herrera, R. Pérez, P. Villar. Special Issue on Genetic Fuzzy Systems and the Interpretability-Accuracy Trade-off. International Journal of Approximate Reasoning. Volume 44, Number 1, February 2007. Table of contents
• O. Cordón, R. Alcalá, J. Alcalá-Fdez, I. Rojas. Special Issue on Genetic Fuzzy Systems: What's Next?. IEEE Transactions on Fuzzy Systems. Volume 15, Number 4, August 2007. Table of contents
• B. Carse, A.G. Pipe. Special Issue on Genetic Fuzzy Systems. International Journal of Intelligent Systems. Volume 22, Number 9, September 2007. Table of contents
• J. Casillas, B. Carse. Special Issue on Genetic Fuzzy Systems: Recent Developments and Future Directions. Soft-Computing Volume 13, Number 5, March 2009. Table of contents
• R. Alcalá, Y. Nojima. Special Issue on Genetic Fuzzy Systems: New Advances. Evolutionary Intelligence Volume 2, Number 1-2, November 2009. Table of contents
• Y. Nojima, R. Alcalá, H. Ishibuchi, F. Herrera. Special Issue on Evolutionary Fuzzy Systems. Soft Computing. Volume 15, Number 12, December 2011. Table of contents
• R. Alcalá, Y. Nojima, H. Ishibuchi and F. Herrera. Special Issue on Evolutionary Fuzzy Systems. International Journal of Computational Intelligence Systems. Volume 5, Number 2, July 2012. Table of contents
• R. Alcalá, Y. Nojima, H. Ishibuchi and F. Herrera. Special Issue on Evolutionary Fuzzy Systems. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems. Volume 20, Number 2, October 2012. Table of contents

The collection of papers that we could find on these special issues give us a historical tour on the different stages we can find in the evolution of GFSs research:

• The two first special issues (1997, 1998) contain contributions devoted to learning KB components using the different learning approaches (Michigan, IRL, Pittsburgh) together with some applications. We can find representative approaches of different areas of the taxonomy.
• In the next two special issues (2001, 2004) we can find contributions that exploit the mentioned genetic learning approaches together with contributions that stress new branches such as genetic rule selection, multiobjective genetic algorithms for rule selection, the use of genetic programming for learning fuzzy systems, hierarchical genetic fuzzy systems, coevolutionary genetic fuzzy systems, the combination of boosting and evolutionary fuzzy systems learning, embedded genetic DB learning, and first studies for dealing with high dimensional problems, among others.
• The next three special issues, published in 2007, emphasize three different directions. Carse and Pipe's special issue collect papers focused in the mentioned areas (multiobjective evolutionary learning, boosting and evolutionary learning, ...) and stress some new ones such as evolutionary adaptive inference systems. Casillas et al.'s special issue is focused on the trade-off between interpretability and accuracy, collecting four papers that proposed different GFSs for tackling this problem. Cordón et al.'s special issue focuses its attention on novel GFS proposals under the title "What's Next?", collecting highly innovative GFS proposals that can mark new research trends. The four collected papers are focused on: a new Michigan approach for learning RBs based on XCS (Casillas J, Carse B, Bull L. (2007) Fuzzy-XCS: A Michigan genetic fuzzy system, IEEE Transactions on Fuzzy Systems 15(4):536-550, doi: 10.1109/TFUZZ.2007.900904), GFSs for imprecisely observed data (low quality data) (Sánchez L, Couso I. (2007) Advocating the use of imprecisely observed data in genetic fuzzy systems, IEEE Transactions on Fuzzy Systems 15(4):551-562, doi: 10.1109/TFUZZ.2007.895942), incremental evolutionary learning of TS-fuzzy systems (Hoffmann F, Schauten D, Hölemann S. (2007) Incremental evolutionary design of TSK fuzzy controllers, IEEE Transactions on Fuzzy Systems 15(4):563-577, doi: 10.1109/TFUZZ.2007.900905), and evolutionary fuzzy rule induction for subgroup discovery (del Jesus MJ, González P, Herrera F, Mesonero M. (2007) Evolutionary fuzzy rule induction process for subgroup discovery: A case study in marketing, IEEE Transactions on Fuzzy Systems 15(4):578-592, doi: 10.1109/TFUZZ.2006.890662).
• The first special issue of 2009, co-edited by J. Casillas and B. Carse, is devoted to new developments, paying attention to multiobjective genetic extraction of linguistic fuzzy rule based systems from imprecise data (Sánchez L, Otero J, Couso I (2009) Obtaining Linguistic Fuzzy Rule-based Regression Models from Imprecise Data with Multiobjective Genetic Algorithms. Soft Computing 13(3):467-479, doi: 10.1007/s00500-008-0362-4), multiobjetive genetic rule selection and tuning (Gacto MJ, Alcalá R, Herrera F (2009) Adaptation and application of multi-objective evolutionary algorithms for rule reduction and parameter tuning of fuzzy rule-based systems. Soft Computing 13(3):419-436, doi: 10.1007/s00500-008-0359-z), parallel distributed genetic fuzzy rule selection (Nojima Y, Ishibuchi H, Kuwajima I (2009) Parallel distributed genetic fuzzy rule selection. Soft Computing 13(3):511-519, doi: 10.1007/s00500-008-0365-1), context adaptation of fuzzy systems (Botta A, Lazzerini B, Marcelloni F, Stefanescu DC (2009) Context Adaptation of Fuzzy Systems Through a Multi-objective Evolutionary Approach Based on a Novel Interpretability Index. Soft Computing 13(3):437-449, doi: 10.1007/s00500-008-0360-6), compact fuzzy systems (Casillas J, Pedro Martínez, Benítez AD (2009) Learning consistent, complete and compact fuzzy rules sets in conjunctive normal form for system identification. Soft Computing 13(3):451-465, doi: 10.1007/s00500-008-0361-5), neuro-coevolutionary GFSs (Regattieri-Delgado M, Yassue-Nagai E, Ramos de Arruda LV (2009) A neuro-coevolutionary GFS to build soft sensors. Soft Computing 13(3):481-495, doi: 10.1007/s00500-008-0363-3), evolutionary learning of TSK rules with variable structure (Mucientes M, Vidal JC, Bugarín A and Lama M (2009) Processing time estimations by variable structure TSK rules learned through genetic programming. Soft Computing 13(3):497-509, doi: 10.1007/s00500-008-0364-2) and genetic fuzzy association rules extraction ( Chen C-H, Hong T-P, Tseng VS, Lee C-S (2009) A genetic-fuzzy mining approach for items with multiple minimum supports. Soft Computing 13(3):521-533, doi: 10.1007/s00500-008-0366-0).
• The five papers in the second 2009 special issue, co-edited by R. Alcalá and Y. Nojima, address distinct subjects focusing on new, significant novel lines of development of GFSs such as, the use of parallel distributed GFSs as a way to address large scale problems (Robles I, Alcalá R, Benítez JM, Herrera F (2009) Evolutionary parallel and gradually distributed lateral tuning of fuzzy rule-based systems. Evolutionary Intelligence 2(1-2):5-19, doi: 10.1007/s12065-009-0025-0), the use of multi-objective evolutionary algorithms to improve the interpretabilityaccuracy trade-off of fuzzy rule-based systems (Antonelli M, Ducange P, Lazzerini B, Marcelloni F (2009) Evolutionary parallel and gradually distributed lateral tuning of fuzzy rule-based systems. Evolutionary Intelligence 2(1-2):21-37, doi: 10.1007/s12065-009-0022-3 and Márquez AA, Márquez FA, Peregrín A (2009) Rule base and adaptive fuzzy operators cooperative learning of Mamdani fuzzy systems with multi-objective genetic algorithms. Evolutionary Intelligence 2(1-2):39-51, doi: 10.1007/s12065-009-0026-z), the design of new learning schemes on new real-world application areas (Walter I, Gomide F (2009) Multiagent coevolutionary genetic fuzzy system to develop bidding strategies in electricity markets: computational economics to assess mechanism design. Evolutionary Intelligence 2(1-2):53-71, doi: 10.1007/s12065-009-0023-2) and a new proposal to adapt genetic fuzzy classification systems to deal with vague data from low quality data sets (Palacios AM, Sánchez L, Couso I (2009) Extending a simple genetic cooperative-competitive learning fuzzy classifier to low quality datasets. Evolutionary Intelligence 2(1-2):73-84, doi: 10.1007/s12065-009-0024-1).
• The special issue of 2011, co-edited by Y. Nojima, R. Alcalá, H. Ishibuchi and F. Herrera, includes some novel extensions of EFS or GFS techniques and real world applications as, determining the appropriate granularities by using data mining-based techniques for multi-objective genetic rule selection and tuning of fuzzy rule-based classifiers (Alcalá R, Nojima Y, Herrera F, Ishibuchi H. (2011) Multiobjective genetic fuzzy rule selection of single granularity-based fuzzy classification rules and its interaction with the lateral tuning of membership functions, Soft Computing 15(12):2303-2318, doi: 10.1007/s00500-010-0671-2), using a genetic fuzzy data mining process with multiple minimum supports (Chen CH, Hong TP, Tseng VS (2011) Genetic-fuzzy mining with multiple minimum supports based on fuzzy clustering, Soft Computing 15(12):2319-2333, doi: 10.1007/s00500-010-0664-1), designing linguistic Mamdani fuzzy systems with a good interpretability-accuracy tradeoff applying an evolutionary multi-objective optimization algorithm (Antonelli M, Ducange P, Lazzerini B, Marcelloni F (2011) Learning knowledge bases of multi-objective evolutionary fuzzy systems by simultaneously optimizing accuracy, complexity and partition integrity, Soft Computing 15(12):2335-2354, doi: 10.1007/s00500-010-0665-0), using a multistage genetic fuzzy classifier for the problem of land cover classification from satellite imagery (Stavrakoudis DG, Theocharis JB, Zalidis GC (2011) A multistage genetic fuzzy classifier for land cover classification from satellite imagery, Soft Computing 15(12):2355-2374, doi: 10.1007/s00500-010-0666-z), applying a co-evolutionary fuzzy system to decision systems for the problem of job negotiation between community-grids (Fölling A, Grimme C, Lepping J, Papaspyrou A (2011) Connecting Community-Grids by supporting job negotiation with coevolutionary Fuzzy-Systems, Soft Computing 15(12):2375-2387, doi: 10.1007/s00500-010-0667-y), tackling the learning from data streams in which concepts vary over time by using Michigan-style learning fuzzy classifier systems (Orriols-Puig A, Casillas J (2011) Fuzzy knowledge representation study for incremental learning in data streams and classification problems, Soft Computing 15(12):2389-2414, doi: 10.1007/s00500-010-0668-x), analyzing the possibilities for modifying multiobjective fuzzy genetics-based machine learning to obtain classifiers with higher training and test data accuracy (Ishibuchi H, Nakashima Y, Nojima Y (2011) Performance evaluation of evolutionary multiobjective optimization algorithms for multiobjective fuzzy genetics-based machine learning, Soft Computing 15(12):2415-2434, doi: 10.1007/s00500-010-0669-9) and finding the relationship between patients and their arrival time at the Psychiatric Emergency Department by using evolutionary subgroup discovery methods (Carmona CJ, González P, del Jesus MJ, Navío-Acosta M, Jiménez-Trevino L (2011) Evolutionary fuzzy rule extraction for subgroup discovery in a psychiatric emergency department, Soft Computing 15(12):2435-2448, doi: 10.1007/s00500-010-0670-3).
• The first special issue of 2012, co-edited by Y. Nojima, R. Alcalá, H. Ishibuchi and F. Herrera, includes contributions to pattern classification, regression, association rule mining, and real-world applications. The first four papers are related to pattern classification problems as, the efficient design of a fuzzy relational rule models by genetic fuzzy rule learning (A. González, R. Pérez, Y. Caises, E. Leyva (2012) An efficient inductive genetic learning algorithm for fuzzy relational rules, IJCIS 5(2):212-230, doi: 10.1080/18756891.2012.685265), generating an ensemble fuzzy classifier from FURIA-based component classifiers by evolutionary multiobjective algorithms using NSGA-II to optimize the combination of the component classifiers with respect to different objective functions (K. Trawinski, O. Cordón, A. Quirin (2012) A study on the use of multiobjective genetic algorithms for classifier selection in FURIA-based fuzzy multiclassifiers, IJCIS 5(2):231-253, doi: 10.1080/18756891.2012.685272), dealing with high dimensional classification problems like hyperspectral satellite images and real-life data sets with a large number of features up to 12600 (D.G. Stavrakoudis, G.N. Galidaki, I.Z. Gitas, J.B. Theocharis (2012) Reducing the complexity of genetic fuzzy classifiers in highly-dimensional classification problems, IJCIS 5(2):254-275, doi: 10.1080/18756891.2012.685290) and proposing the generalization of several preprocessing methods to be used together with a GFS for low quality imbalanced data sets (A.M. Palacios, L. Sánchez, I. Couso (2012) Equalizing imbalanced imprecise datasets for genetic fuzzy classifiers, IJCIS 5(2):276-296, doi: 10.1080/18756891.2012.685292). The last six papers are related to regression problems, association rule mining, and real-world applications as, incorporating an adaptive threshold model into the optimization of rule weights by evolutionary multiobjective optimization (A.A. Márquez, F.A. Márquez, A. Peregrín (2012) A mechanism to improve the interpretability of linguistic fuzzy systems with adaptive defuzzification based on the use of a multi-objective evolutionary algorithm, IJCIS 5(2):297-321, doi: 10.1080/18756891.2012.685309), the inclusion of an adaptive immune algorithm within a multi-objective optimization framework with a variable length coding scheme for regression (J. Chen and M. Mahfouf (2012) Improving transparency in approximate fuzzy modeling using multi-objective immune-inspired optimisation, IJCIS 5(2):322-342, doi: 10.1080/18756891.2012.685311), applying SPEA2 to fuzzy association rule mining by maximizing the shape suitability of the membership functions and the total number of large 1-itemsets (C.H. Chen, T.P. Hong, V.S. Tseng (2012) Finding pareto-front membership functions in fuzzy data mining, IJCIS 5(2):343-354, doi: 10.1080/18756891.2012.685314), the combination of the 2-tuple linguistic representation and genetic lateral tuning into CHC algorithm-based subgroup discovery (C.J. Carmona, P. González, M.J. Gacto, M.J. del Jesus (2012) Genetic lateral tuning for subgroup discovery with fuzzy rules using the algorithm NMEEF-SD, IJCIS 5(2):355-367, doi: 10.1080/18756891.2012.685323), using color information and genetic tuning of fuzzy membership functions to improve laser pointer spot detection for an userfriendly and less expensive home device control device system (F. Chávez, F. Fernández, M.J. Gacto, R. Alcalá (2012) Automatic laser pointer detection algorithm for environment control device systems based on template matching and genetic tuning of fuzzy rule-based systems, IJCIS 5(2):368-386, doi: 10.1080/18756891.2012.685327) and the application of GFSs to an e-learning system which predicts students' performance and understands students' learning behavior (Ángela Nebot, Francisco Mugica, Félix Castro and Jesús Acosta (2012) Genetic learning of fuzzy parameters in predictive and decision support modelling, IJCIS 5(2):387-402, doi: 10.1080/18756891.2012.685328).
• The second special issue of 2012, co-edited by Y. Nojima, R. Alcalá, H. Ishibuchi and F. Herrera, includes recent novel contributions to pattern classification, regression, association rule mining and real-world applications. The first four papers are related to pattern classification problems, as a fuzzy decision tree classifier in which fuzzy the partitions associated with the linguistic terms used are built with the help of ignorance functions (J. Sanz, H. Bustince, A. Fernández and F. Herrera IIVFDT: Ignorance Functions Based Interval-valued Fuzzy Decision Tree With Genetic Tuning, IJUFKS 20(2):1-30, doi: 10.1142/S0218488512400132), a filter based approach for constructing features by using a genetic algorithm (David Garcia, Antonio Gonzalez and Raul Perez (2012) A Filter Proposal For Including Feature Construction In A Genetic Learning Algorithm, IJUFKS 20(2):31-49, doi: 10.1142/S0218488512400144), a modification of the Adaboost algorithm to generate FRBCs when dealing with low quality imbalanced datasets (Ana Palacios, Luciano Sanchez and Ines Couso (2012) Combining Adaboost With Preprocessing Algorithms For Extracting Fuzzy Rules From Low Quality Data In Possibly Imbalanced Problems, IJUFKS 20(2):51-71, doi: 10.1142/S0218488512400156), a hierarchical genetic FRBS for high dimensional classification problems (Dimitris G. Stavrakoudis and John B. Theocharis (2012) Handling Highly-dimensional Classification Tasks With Hierarchical Genetic Fuzzy Rule-based Classifiers, IJUFKS 20(2):73-104, doi: 10.1142/S0218488512400168). The next three papers are related to regression problems. The first two papers makes use of non-standard structures, as fuzzy hierarchical models combined with a bacterial memetic programming algorithm (Krisztián Balázs and László T. Kóczy (2012) Hierarchical-interpolative Fuzzy System Construction By Genetic And Bacterial Memetic Programming Approaches, IJUFKS 20(2):105-131, doi: 10.1142/S021848851240017x) and fuzzy regression trees combined with artificial immune systems (Fathi Gasir, Keeley Crockett and Zuhair Bandar (2012) Inducing Fuzzy Regression Tree Forests Using Artificial Immune Systems, IJUFKS 20(2):133-157, doi: 10.1142/S0218488512400181). The last one tries to improve the interpretability or transparency of a fuzzy regression model by using multiobjective optimization algorithms (M. Isabel Rey, Marta Galende, M. J. Fuente and Gregorio I. Sainz-Palmero (2012) Checking Orthogonal Transformations And Genetic Algorithms For Selection Of Fuzzy Rules Based On Interpretability-accuracy Concepts, IJUFKS 20(2):159-186, doi: 10.1142/S0218488512400193). The next paper is related to fuzzy association rule mining. It proposes an advanced multiple-level genetic-fuzzy mining algorithm for mining membership functions and fuzzy association rules using multiple-concept levels (Chun-hao Chen, Tzung-pei Hong and Yeong-chyi Lee (2012) Genetic-fuzzy Mining With Taxonomy, IJUFKS 20(2):187-205, doi: 10.1142/S021848851240020x). The last three papers are real-world applications, in which GFSs are applied to interesting real-world problems as removing mixed gaussian and impulse noise from an image (Daoyuan Zhai, Minshen Hao and Jerry Mendel (2012) Universal Image Noise Removal Filter Based On Type-2 Fuzzy Logic System And Qpso, IJUFKS 20(2):207-232, doi: 10.1142/S0218488512400211), modelling fish habitat preferences (Shinji Fukuda and Bernard De Baets (2012) Do Absence Data Matter When Modelling Fish Habitat Preference Using A Genetic Takagi-sugeno Fuzzy Model?, IJUFKS 20(2):233-245, doi: 10.1142/S0218488512400223) and applying fuzzy markup language, fuzzy ontology and genetic learning of linguistic rule bases for healthy diet assessment (Chang-shing Lee, Mei-hui Wang, Hani Hagras, Zhi-wei Chen, Shun-teng Lan, Chin-yuan Hsu, Su-e Kuo, Hui-ching Kuo and Hui-hua Cheng (2012) A Novel Genetic Fuzzy Markup Language And Its Application To Healthy Diet Assessment, IJUFKS 20(2):247-278, doi: 10.1142/S0218488512400235).

GFS Studies on the ISI Web of Science

GFSs Visibility at the ISI Web of Science: Publications and Citations.

The ISI Web of Science provides seamless access to current and retrospective multidisciplinary information from approximately 8,700 of the most prestigious, high impact research journals in the world. Web of Science also provides a unique search method, cited reference searching. With it, users can navigate forward, backward, and through the literature, searching all disciplines and time spans to uncover all the information relevant to their research. Users can also navigate to electronic full-text journal articles (http://scientific.thomson.com/products/wos/). In the link of "Advanced Search", we consider the query:

TS = (("GA-" OR "GA based" OR evolutionary OR "genetic algorithm*" OR "genetic programming" OR "evolution strate*" OR "genetic learning" OR "particle swarm" OR "differential evolutio*" OR "ant system*" OR "ant colony" OR "genetic optimi*" OR "estimation of distribution algorithm*") AND ("fuzzy rule*" OR "fuzzy system*" OR "fuzzy neural" OR "neuro-fuzzy" OR "fuzzy control*" OR "fuzzy logic cont*" OR "fuzzy class*" OR "fuzzy if" OR "fuzzy model*" OR "fuzzy association rule*" OR "fuzzy regression"))

TS field is a search based on the "Topic". The numerical results of the query are:

Date of analysis: July 3th, 2014
Number of papers: 7423
Sum of the times cited: 43317
Average citations per item: 7.30

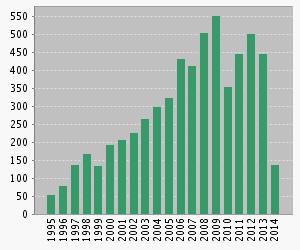
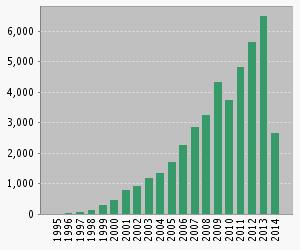
Figures 12 and 13 show the number of publications and citations per year.

Fig. 12. Publications in GFS per year (Web of Science)	Fig. 13. Number of citations per year (Web of Science)

We observe an increasing number of publications per year with more than 300 papers per year in the last five ones. The number of citations shows a similar increasing trend in recent years. All this data can allow us to say the field of GFSs has now reached a stage of maturity after the earliest papers published at 1991, and there are also many basic issues yet to be resolved and there is an active and vibrant worldwide community of researchers working on these issues.
 

Highly cited papers and GFS Studies on the ISI Web of Science.

The search on the ISI Web of Science allows us to get the ten most cited papers that can provide a picture on ten important contributions on the topic that are representative approaches of different taxonomy areas. In the following, we present this study on the most cited articles divided in two periods: articles until 2000 and articles from 2001 to 2010 (July 6th)

First period - until 2000.

Figure 14 shows the list of ten papers in the first period (we should note that we have eliminated a paper devoted to a survey on neuro-fuzzy rule generation that is not devoted to GFSs). Following, we shortly describe them, paying attention to the associated area of the taxonomy and the used learning approach.

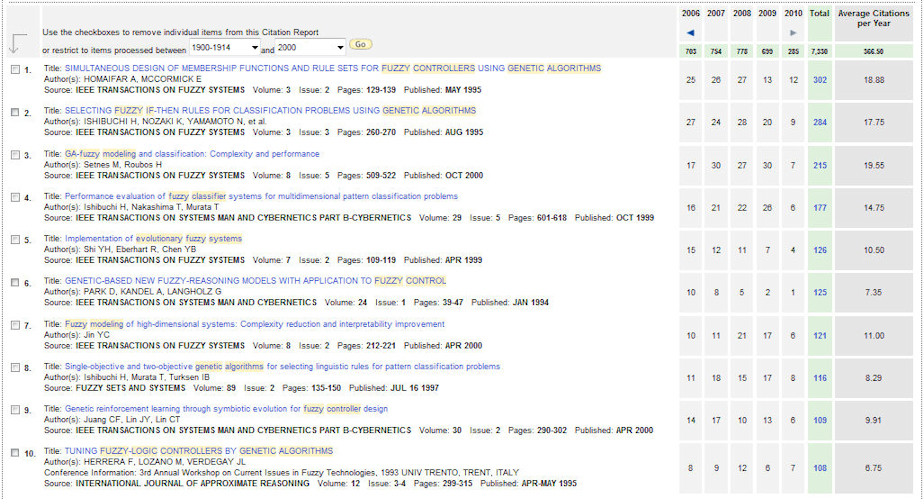
Fig. 14 GFS ten most cited papers until 2000 (Date: 6th July 2010)

• Homaifar and Mccormick's paper (IEEE TFS, 302 cites)

Homaifar A, Mccormick E (1995) Simultaneous design of membership functions and rule sets for fuzzy controllers using genetic algorithms. IEEE Transactions on Fuzzy Systems 3(2):129-139, doi: 10.1109/91.388168.

Authors proposed the use of GAs to learn a complete KB for control problems, determining both membership functions and RB together in order to address their co-dependency (KB learning). They considered the simple GA for a Pittsburgh approach, with integer coding for rule consequents (similar to Thrift's proposal) and integer coding for membership function support amplitude (5 different amplitude values) in the same chromosome. This contribution is a reference in the topic as a classic Pittsburgh approach for genetic KB learning.

• Ishibuchi, Nozaki, Yamamoto et al.'s paper (IEEE TFS, 284 cites)

Ishibuchi H, Nozaki K, Yamamoto N, Tanaka H (1995) Selection fuzzy IF-THEN rules for classification problems using genetic algorithms. IEEE Transactions on Fuzzy Systems 3(3): 260-270, doi: 10.1109/91.413232.

GAs are used for selecting a small number of fuzzy IF-THEN rules with high classification performance. The proposed algorithm was based on a simple GA with binary coding representing whether a rule should be selected or not from an initial set of candidate rules (obtained from a predefined DB by applying a simple data-driven method). The problem was formulated as a combinatorial optimization problem with two objectives considered by a weighted fitness function: to maximize the number of correctly classified patterns and to minimize the number of rules. This contribution is the most classic contribution for genetic rule selection and one of the departure points for studies in the trade-off between interpretability and accuracy.

• Setnes and Roubos' paper (IEEE TFS, 215 cites)

Setnes M, Roubos H (2000) GA-fuzzy modeling and classification: complexity and performance. IEEE Transactions on Fuzzy Systems 8(5):509-522, doi: 10.1109/91.873575.

A two-step approach was proposed for function approximation, dynamic systems modeling and data classification problems by learning approximate TS-rules. First, fuzzy clustering was applied to obtain a compact initial KB. Then this model is optimized by a real-coded GA subjected to constraints in order to maintain the semantic properties of the rules. Each chromosome represents the parameters defining each fuzzy model (membership functions of the antecedents and coefficients of the consequents), thus performing a tuning of the initial model. This approach was also combined with an iterative similarity-driven rule base simplification algorithm as an intermediate stage between KB generation and parameter optimization. This is an important contribution that uses GAs for tuning inside a hybrid method, trying to get a more interpretable approximate TS model.

• Ishibuchi, Nakashima and Murata's paper (IEEE TSMC-B, 177 cites)

Ishibuchi H, Nakashima T, Murata T (1999) Performance evaluation of fuzzy classifier systems for multidimensional pattern classification problems. IEEE Transactions on Systems, Man and Cybernetics. Part B-Cybernetics 29(5):601-618, doi: 10.1109/3477.790443.

Authors presented a genetics-based machine learning method that automatically learns a linguistic RB for pattern classification problems from numerical data. In this method, each linguistic IF-THEN rule is handled as a chromosome. Integer coding was considered to represent the rule antecedents (including the don't care symbol) and the heuristic method proposed in (Ishibuchi H, Nozaki K, Yamamoto N, Tanaka H (1995) Selection fuzzy IF-THEN rules for classification problems using genetic algorithms. IEEE Transactions on Fuzzy Systems 3(3): 260-270, doi: 10.1109/91.413232 ) was used to automatically generate the consequent class and certainty factor for each antecedent combination. A fitness value was assigned to each rule. The evolution is not based on the performance of an entire rule set, the solution is not the final population but the best population. It follows a GCCL approach being an important contribution for learning RBs.

• Shi, Eberhart, Chen's paper (IEEE TFS, 126 cites)

Shi YH, Eberhart R, Chen YB (1999) Implementation of evolutionary fuzzy systems. IEEE Transactions on Fuzzy Systems 7(2):109-119, doi: 10.1109/91.755393.

A new GFS was proposed for classification, using a GA for evolving the membership function parameters and, the type and the RB including the number of rules inside it. In addition, a fuzzy expert system was designed from the experience and knowledge and was used to adapt the genetic parameters of the GA. The chromosome was a mixture considering all the parts of the linguistic FRBS by using integer coding and following a Pittsburgh approach. This is an interesting approach for evolving KB components for classification problems.

• Park, Kandel and Langholz's paper (IEEE TSMC, 125 cites)

Park D, Kandel A, Langholz G (1994) Genetic-based new fuzzy-reasoning models with applications to fuzzy control. IEEE Transactions on Systems, Man and Cybernetics 24(1):39-47, doi: 10.1109/21.259684.

A new fuzzy reasoning method was used to enhance the performance of fuzzy controllers obtained from prior knowledge provided by an expert. To avoid initial subjective selection of fuzzy reasoning models, the authors proposed the use of GAs to find simultaneously the optimal fuzzy relation matrix (used in the new fuzzy reasoning method, extending Pham and Karaboga's proposal) and the fuzzy membership functions. In this way, each chromosome is divided into two parts, one for the fuzzy relation matrix and another for the fuzzy membership functions of the DB, following a Pittsburgh approach. It is a classic paper using fuzzy relations for evolving a KB that can be considered as a tuning approach since it considers the prior knowledge provided by the experts.

• Jin, YC's paper (IEEE TFS, 121 cites)

Jin, YC (2000) Fuzzy modeling of high-dimensional systems: Complexity reduction and interpretability improvement. IEEE Transactions on Fuzzy Systems 8(2):212-221,

Jin proposes an approach to data-based Linguistic Fuzzy Modelling of high-dimensional systems. He reduces the number of rules, removing redundant rules by means of a fuzzy similarity measure, called similarity of rule premise. Moreover, the author proposes a methodology based on genetic algorithms and the gradient learning method. Jin presents a regularization learning to reduce the number of fuzzy sets. ``The regularization is to drive the similar fuzzy sets to the same fuzzy set during gradient learning so that the interpretability of the fuzzy system can be greatly improved without seriously deteriorating the system performance". This approach mixes tuning and rule merging strategies as a way to optimize the structure and parameters of the fuzzy system.

• Ishibuchi, H and Murata, T and Turksen, IB's paper (FSS, 116 cites)

Ishibuchi H, Murata T, Turksen IB (1997) Single-objective and two-objective genetic algorithms for selecting linguistic rules for pattern classification problems. Fuzzy Sets and Systems 89(2):135-150,

This paper proposes various methods for constructing a compact fuzzy classification system consisting of a small number of linguistic classification rules. The authors study both, single-objective and two-objective genetic algorithms, to perform the rule selection on an initial set of classification rules involving "don't care" conditions and considering the aforementioned objectives: to maximize the classification accuracy and to minimize the number of rules. This contribution is the most classic contribution for multi-objective genetic rule selection extending the ideas in (Ishibuchi H, Nozaki K, Yamamoto N, Tanaka H (1995) Selection fuzzy IF-THEN rules for classification problems using genetic algorithms. IEEE Transactions on Fuzzy Systems 3(3): 260-270, doi: 10.1109/91.413232 ) to a multi-objective framework.

• Juang, Ling and Ling's paper (IEEE TSMC-B, 2000, 109 cites)

Juang CF, Lin JY, Lin CT (2000) Genetic reinforcement learning through symbiotic evolution for fuzzy controller design. IEEE Transactions on Systems, Man and Cybernetics. Part B-Cybernetics 30(2):290-302, doi: 10.1109/3477.836377.

A new genetic reinforcement learning algorithm was proposed in this contribution, the Symbiotic Evolution (Moriarty DE, Miikkulainen R (1996) Efficient reinforcement learning through symbiotic evolution. Machine Learning 22:11-32, doi: 10.1007/BF00114722) based fuzzy controller. Each chromosome represents a single TS-type rule, and an n-rule fuzzy system is constructed by selecting chromosomes from the population. In this way, a real coding was used to represent each rule by encoding the parameters of local semantics-based Gaussian-type membership functions and the associated coefficients of the consequent part. It is an interesting GCCL approach for evolving an approximate FRBS.

• Herrera, Lozano and Verdegay's paper (IJAR, 108 cites)

Herrera F, Lozano M, Verdegay JL (1995) Tuning fuzzy-logic controllers by genetic algorithms. International Journal of Approximate Reasoning 12(3-4):299-315, doi: 10.1016/0888-613X(94)00033-Y.

Authors proposed a tuning method for obtaining high-performance fuzzy control rules by means of GAs. The tuning method locally fits the membership functions of the fuzzy rules dealing with the parameters of the membership functions. A chromosome represents the parameters of the membership functions used by each rule in the initial KB, the chromosome represents the concatenated rule parameters. This is the first proposal for getting an approximate FRBS via tuning associated to the rules.

Second period - recent papers, 2001 to 2010 (July 6th).

Figure 15 shows the list of ten papers (we should note that we have eliminated some papers that are not devoted to GFSs, i.e., papers devoted to other techniques that references to GFSs at any part of them). In the following, we shortly describe the 10 most cited papers of this second period, paying attention to the associated area of the taxonomy and the used learning approach.

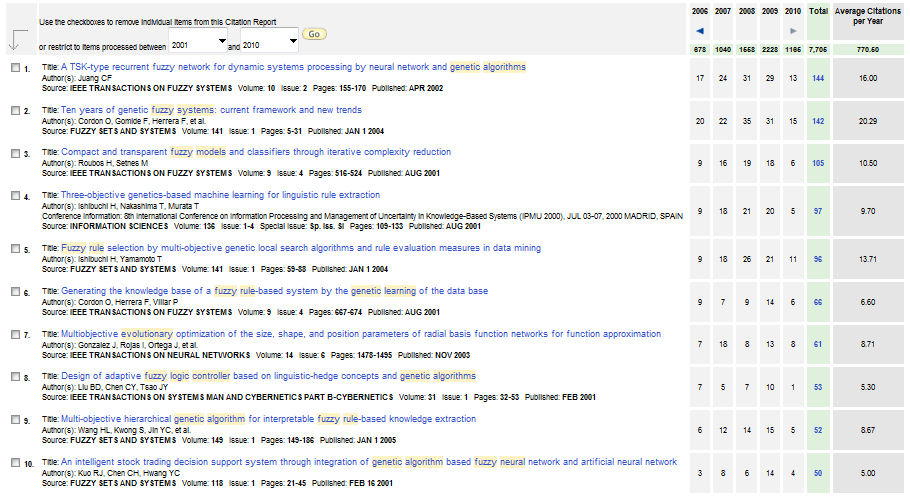
Fig. 15 GFS ten most cited papers from 2001 to present (Date: 6th July 2010)

• Juang's paper (IEEE TFS, 144 cites)

Juang, CF (2002) A TSK-type recurrent fuzzy network for dynamic systems processing by neural network and genetic algorithms. IEEE Transactions on Fuzzy Systems 10(2):155-170,

This paper proposes a TSK-type recurrent fuzzy network structure designed by either neural network or genetic algorithms depending on the learning environment. Set forth first is a recurrent fuzzy network which develops from a series of recurrent fuzzy if-then rules with TSK-type consequent parts. Network design under different learning environments is next advanced. For problems where supervised training data is directly available, neural network learning approach is adopted. An online learning algorithm with concurrent structure and parameter learning is proposed. As to the problems where gradient information for neural network learning is costly to obtain or unavailable, like reinforcement learning, TSK-type recurrent fuzzy network with Genetic learning is put forward. The precondition parts are partitioned in a flexible way, and all free parameters are designed concurrently by genetic algorithm. This last algorithm, the one with genetic learning, was applied to dynamic system control. This approach is devoted to the genetic tuning of the parameters of neuro-fuzzy systems.

• Cordon and Gomide and Herrera and Hoffmann and Magdalena's paper (FSS, 142 cites)

Cordon O, Gomide F, Herrera F, Hoffmann F, Magdalena L (2004) Ten years of genetic fuzzy systems: current framework and new trends. Fuzzy Sets and Systems 141(1):5-31, doi: 10.1016/S0165-0114(03)00111-8.

Cordon et all propose the first review in the topic of Genetic Fuzzy Systems. The paper provides an account of GFSs, with special attention to genetic FRBSs. After a brief introduction to models and applications of GFSs, the field was overviewed, new trends were identified, a critical evaluation of genetic fuzzy systems for fuzzy knowledge extraction was elaborated, and open questions that remain to be addressed in the future were raised. The paper also includes some of the key references required to quickly access implementation details of genetic fuzzy systems.

• Roubos and Setnes's paper (IEEE TFS, 105 cites)

Roubos H, Setnes M (2001) Compact and transparent fuzzy models and classifiers through iterative complexity reduction. IEEE Transactions on Fuzzy Systems 9(4):516-524,

As it is well-known, GAs provide a powerful tool to increase the accuracy of fuzzy models for both systems modeling and classification. In this work, the authors explore the GA to find redundancy in the fuzzy model for the purpose of model reduction. An aggregated similarity measure is applied to search for redundancy in the rule base description. As a result, they propose an iterative fuzzy identification technique starting with data-based fuzzy clustering with an overestimated number of local models. The GA is then applied to find redundancy among the local models with a criterion based on maximal accuracy and maximal set similarity. After the reduction steps, the GA is applied with another criterion searching for minimal set similarity and maximal accuracy. This results in an automatic identification scheme with fuzzy clustering, rule base simplification and constrained genetic optimization with low-human intervention. Attractive models with respect to compactness, transparency and accuracy, are the result of this symbiosis where GAs are applied for rule reduction a parameter tuning by merging of the membership functions.

• Ishibuchi and Yamamoto's paper (IS, 97 cites)

Ishibuchi H, Nakashima T, Murata T (2001) Three-objective genetics-based machine learning for linguistic rule extraction. Information Sciences 136(1-4):109-133,

One difficulty in the handling of high-dimensional problems by fuzzy rule-based systems is the exponential increase in the number of fuzzy rules with the number of input variables. Another difficulty is the deterioration in the comprehensibility of fuzzy rules when they involve many antecedent conditions. Ishibuchi et al present a multi-objective evolutionary algorithm for classification problems with three objectives: maximizing the number of correctly classified patterns, minimizing the number of rules and minimizing the number of antecedent conditions. In this contribution, they show two genetic-algorithm-based approaches. One is rule selection where a small number of linguistically interpretable fuzzy rules are selected from a large number of prespecified candidate rules. The other is fuzzy genetics-based machine learning where rule sets are evolved by genetic operations. These two approaches search for non-dominated rule sets with respect to the said three objectives.

• Ishibuchi and Yamamoto's paper (FSS, 96 cites)

Ishibuchi H, Yamamoto T (2004) Fuzzy rule selection by multi-objective genetic local search algorithms and rule evaluation measures in data mining. Fuzzy Sets and Systems 141(1):59-88, doi: 10.1016/S0165-0114(03)00114-3.

Ishibuchi et al apply an improved multi-objective evolutionary algorithm, the Multi-Objective Genetic Local Search (MOGLS) for classification problems, considering the same approach for multi-objective fuzzy rule selection shown in (Ishibuchi H, Nakashima T, Murata T (2001) Three-objective genetics-based machine learning for linguistic rule extraction. Information Sciences 136: 109-133) and three objectives: maximizing the number of correctly classified training patterns, minimizing the number of fuzzy rules, and minimizing the total rule length of fuzzy rules. Their main contribution is that they propose to use two well-known data mining criteria (confidence and support) as prescreening criteria, in order to find a tractable number of candidate fuzzy if-then rules. Through computer simulations, they demonstrate that such a prescreening procedure improves the efficiency of fuzzy rule selection. Furthermore, a learning algorithm of rule weights (i.e., certainty factors) is also combined with their MOGLS algorithm.

• Cordon and Herrera and Villar's paper (IEEE TFS, 66 cites)

Cordon O, Herrera F, Villar P (2001) Generating the knowledge base of a fuzzy rule-based system by the genetic learning of the data base. IEEE Transactions on Fuzzy Systems 9(4):667-674,

In this contribution, a new method is proposed to automatically learn the KB by finding an appropiate DB by means of a GA while using a simple generation method to derive the RB. The genetic process learns the number of linguistic terms per variable (granularity) and the membership function parameters that define their semantics (three parameters per membership function since they consider triangular-shaped membership functions), while a rule base generation method learns the number of rules and their composition. In this way, they present a model for embedded evolutionary learning of the DB in regression problems.

• Gonzalez and Rojas and Ortega's paper (IEEE TNN, 61 cites)

Gonzalez J, Rojas I, Ortega J, Pomares H, Fernandez J, Diaz AF (2003) Multiobjective evolutionary optimization of the size, shape, and position parameters of radial basis function networks for function approximation. IEEE Transactions on Neural Networks 14(6):1478-1495, doi: 10.1109/TNN.2003.820657.

This paper presents a multiobjective evolutionary algorithm to optimize radial basis function neural networks in regression problems based on input-output pairs. The procedure allows the application of heuristics to improve the solution of the problem at hand by including some new genetic operators in the evolutionary process. These new operators are based on two well-known matrix transformations: singular value decomposition and orthogonal least squares, which have been used to define new mutation operators that produce local or global modifications in the radial basis functions of the networks (the individuals in the population in the evolutionary procedure). After analyzing the efficiency of the different operators, they show that the global mutation operators yield an improved procedure to adjust/tune the parameters of the radial basis function neural networks.

• Liu and Chen and Tsao's paper (IEEE TSMC-B, 53 cites)

Liu BD, Chen CY, Tsao JY (2001) Design of adaptive fuzzy logic controller based on linguistic-hedge concepts and genetic algorithms. IEEE Transactions on Systems Man and Cybernetics Part B-Cybernetics 31(1):32-53,

The authors propose a novel fuzzy logic controller, called linguistic hedge fuzzy logic controller, to simplify the membership function constructions and the rule developments. The design methodology is a hybrid model based on the concepts of the linguistic hedges and GAs. The linguistic hedge operators are used to adjust the shape of the membership functions dynamically. GAs are adopted to search the optimal linguistic hedge combination in the linguistic hedge module. The Linguistic hedge module associated with the GA enables it to be adaptive with low design complexity and small hardware overhead. The proposed approach is applied to design three well-known nonlinear systems.

• Wang and Kwong and Jin's paper (FSS, 52 cites)

Wang HL, Kwong S, Jin YC, et al. (2005) Multi-objective hierarchical genetic algorithm for interpretable fuzzy rule-based knowledge extraction. Fuzzy Sets And Systems 149(1):149-186, doi: 10.1016/j.fss.2004.07.013.

A new scheme based on multi-objective hierarchical GA is proposed in this paper to extract interpretable rule-based knowledge from data. The approach is derived from the use of multiple objective genetic algorithm, where the genes of the chromosome are arranged into control genes and parameter genes. These genes are in a hierarchical form so that the control genes can manipulate the parameter genes in a more effective manner. The effectiveness of this chromosome formulation enables the fuzzy sets and rules to be optimally reduced. Some important concepts about the interpretability are introduced and the fitness function in the multi-objective GA consider both the accuracy and interpretability of the fuzzy model. In order to remove the redundancy of the rule base proactively, they also apply an interpretability-driven simplification method to newborn individuals. The method is divided into two main parts. Fuzzy clustering is first applied to generate an initial rule-based model. Then the multi-objective hierarchical GA and the recursive least square method are used to obtain the optimized fuzzy models.

• Kuo and Chen and Hwang's paper (FSS, 50 cites)

Kuo RJ, Chen CH, Hwang YC (2001) An intelligent stock trading decision support system through integration of genetic algorithm based fuzzy neural network and artificial neural network. Fuzzy Sets and Systems 118(1):21-45,

The stock market, which has been investigated by various researchers, is a rather complicated environment. Most research only concerned the technical indexes (quantitative factors), instead of qualitative factors, e.g., political effect. However, the latter plays a critical role in the stock market environment. This contribution proposes a GA based fuzzy neural network to formulate the KB of fuzzy inference rules which can measure the qualitative effect on the stock market. Next, the effect is further integrated with the technical indexes through the artificial neural network. An example based on the Taiwan stock market is utilized to assess the proposed intelligent system. Evaluation results in the paper indicate that the neural network considering both the quantitative and qualitative factors (by using GFSs formulation) excels the neural network considering only the quantitative factors both in the clarity of buying-selling points and buying-selling performance.

MOEFSs: Introduction, Taxonomy and Further Developments

This section presents an overview on Multi-Objective Evolutionary Fuzzy Systems (MOEFSs) and introduces a two-level taxonomy outlined according to the main contributions on this field.

• Introduction
• MOEFSs Taxonomy
• The Accuracy-Interpretability Trade-Off
• Open problems and further developments

Introduction

In some real problems it is difficult to express all the aspects by means of a single objective. For this reason multi-objective optimization has become very popular in the last few years and its application is continuously increasing (Deb K, (2001) Multi-Objective Optimization Using Evolutionary Algorithms. John Wiley & Sons, Inc., New York, USA , Coello CAC, Lamont GB, Veldhuizen DAV (2006) Evolutionary Algorithms for Solving Multi-Objective Problems (Genetic and Evolutionary Computation). Springer-Verlag, Secaucus, NJ, USA). A considerable amount of papers and books has been published in this research area, now named Evolutionary Multi-Objective Optimization (EMOO). EMOO usually involves multiple contradictory objectives to be optimized simultaneously, thus there is no longer a single optimal solution but rather a set of feasible solutions of equivalent quality and each solution represents a trade-off between the conflicting objectives. Initially, GFSs were mainly used to design FRBSs with high accuracy in problems such as classification and control, but later on the need to include multiple objectives arose (Ishibuchi H, Murata T, Turksen IB (1997) Single-objective and two-objective genetic algorithms for selecting linguistic rules for pattern classification problems. Fuzzy Sets Syst 89(2):135-150, doi: 10.1016/S0165-0114(96)00098-X). As stated above, in a multi-objective problem objectives are often conflicting, thus a multi-objective evolutionary algorithm generates a set of fuzzy systems and each of them has a different trade-off between objectives. The chosen objectives depend on the aim of the designed fuzzy system. The primary one is the accuracy of the system with respect to a performance metric, the other objectives can be the complexity of the system, the cost, the computational time, additional performance metrics, etc. As for Evolutionary algorithms, Multi-Objective Evolutionary Algorithms can be used for the automatic learning of FRBSs. The hybridization between these two systems is currently known as MOEFS.

MOEFSs Taxonomy

In the last decades, a great amount of contributions dealing with MOEFSs have been published. Intending to show a well-established framework, we present a two-level taxonomy to classify contributions (figure 16), in which the first level is based on the multiobjective nature of the problem faced, i.e, the type of objectives used, and the second level is based on the type of FRBS components optimized during the evolutionary process. Both of them determine the search space type and complexity, which involve different considerations when applying MOEFSs.

• MOEFSs designed to generate FRBSs with different Accuracy-Interpretability trade-offs. In this case at least one of the objectives is always related to the interpretability of the obtained model, regardless of the problem considered. A considerable number of papers can be found in this group, since the interpretability is one of the most important aspects of FRBSs. While the accuracy is difficult to improve, the interpretability is easy to get, since interpretable models can be given even by hand. These differences between both types of objectives influence the optimization process.
• MOEFSs designed for multi-objective control problems. The considered objectives strictly depend on the particular kind of problem that is taken into account and usually all of them are related with performance issues of the control system. Therefore, the trade-off and the search space will be different and dependent on the problem itself.
• MOEFSs designed for Fuzzy Association Rule Mining. The aim of rule mining is to find a set of fuzzy association rules that reliably represents the knowledge hidden in a data base. In this case, the objectives are used to describe the quality of the obtained rules, i.e. their accuracy and interestingness. To this end, support and confidence are the major factors in measuring the quality of an association rule, but other metrics exists. The aim of the optimization process is not only to improve the general trade-off between objectives for the whole set of rules, but also to obtain a great number of rules, each of them satisfying the objectives at different degrees.

A detailed description of the proposed MOEFSs taxonomy can be found at the following page.

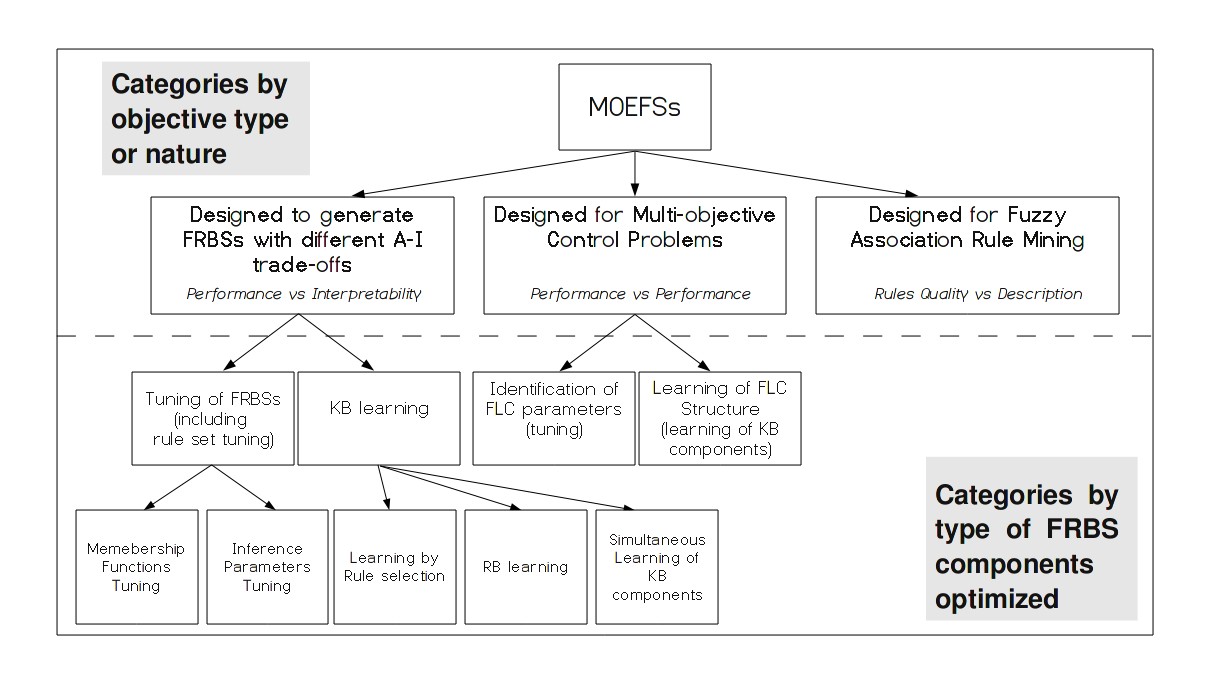
Fig. 16. A two-level taxonomy based on the type of the objectives used (1st level) and on the type of FRBS components optimized (2nd level)

The Accuracy-Interpretability Trade-Off

Considering the importance of the accuracy-interpretability tradeoff for the research community, the category containing the greatest number of contributions is the first one. Initially, the interpretability of the obtained models was neglected, since single-objective EAs permit the optimization of only a single metric. The problem of improving accuracy while maintaining or even improving the interpretability of a fuzzy model was first faced in the mid-1990s by Ishibuchi and his group (Ishibuchi H, Murata T, Turksen IB (1997) Single-objective and two-objective genetic algorithms for selecting linguistic rules for pattern classification problems. Fuzzy Sets Syst 89(2):135-150, doi: 10.1016/S0165-0114(96)00098-X), and the comprehensibility of fuzzy models began to be integrated into the optimization process, thanks to the application of MOEAs to fuzzy systems. Ever since, interpretability has acquired an increasing importance in the field of MOEFSs.

Because of its subjectivity, the main problem is to find a shared definition of interpretability and to measure this characteristic in the obtained models, since several issues need to be taken into account to obtain a human-interpretable model. Over the course of the past decade, several works have analyzed the interpretability problem in FRBSs (O. Cordón (2011) Historical Review of Evolutionary Learning Methods for Mamdani-type Fuzzy Rule-based Systems: Designing Interpretable Genetic Fuzzy Systems: Designing Interpretable Genetic Fuzzy Systems. International Journal of Approximate Reasoning 52(6):894-913, doi: 10.1016/j.ijar.2011.03.004), looking for interpretability measures that could be universally accepted by the research community. Despite this, there are still no commonly accepted measures, and even the terms used in the area (comprehensibility, readability, completeness, consistency, etc.) are confusing and used as synonyms, even if they refer to different concepts. Nowadays, researchers agree on the need to consider two groups of interpretability measures:

• Complexity-based interpretability measures, which are used to decrease the complexity of the fuzzy model (number of rules, number of antecedents in a rule, etc.).
• Semantic-based interpretability measures, which are used to preserve the semantics associated with membership functions (distinguishability, coverage, etc.) and rules (consistency, etc.).

Classically, interpretability indices have only focused on the former group, when evaluating the overall interpretability of a fuzzy model. On the other hand, the definition of good semantic interpretability measures is still an open problem, since they are strongly affected by subjectivity. To this end, several indices have been proposed recently (José M. Alonso and Luis Magdalena and Gil González Rodríguez (2009) Looking for a good fuzzy system interpretability index: An experimental approach. International Journal of Approximate Reasoning 51:115-134 doi: 10.1016/j.ijar.2009.09.004, M. Antonelli, P. Ducange, B. Lazzerini, F. Marcelloni (2011) Learning concurrently data and rule bases of Mamdani fuzzy rule-based systems by exploiting a novel interpretability index. Soft Computing 15(10):1981-1998 doi: 10.1007/s00500-010-0629-4, M.J. Gacto, R. Alcalá and F. Herrera (2010) Integration of an Index to Preserve the Semantic Interpretability in the Multiobjective Evolutionary Rule Selection and Tuning of Linguistic Fuzzy Systems. IEEE Transactions on Fuzzy Systems 18(3):515-531 doi: 10.1109/TFUZZ.2010.2041008). A wider discussion about interpretability in linguistic FRBSs can be found here.

In the following, we can find some significant and/or recent papers that make use of MOEAs to improve the trade-off between interpretability and accuracy of linguistic FRBSs on different topics. They are: Rule Selection (first 2 papers) and Tuning (next 3 papers) approaches to tackle the complexity of FRBSs, KB learning (next 3 papers) to tackle the complexity of FRBSs and tackling the semantic interpretability of linguistic FRBSs (last paper):

Ishibuchi H, Nakashima T, Murata T, Three-objective genetics-based machine learning for linguistic rule extraction. Information Sciences 136:1-4 (2001) 109-133,

Ishibuchi H, Yamamoto T, Fuzzy rule selection by multi-objective genetic local search algorithms and rule evaluation measures in data mining. Fuzzy Sets and Systems 141:1 (2004) 59-88,  doi: 10.1016/S0165-0114(03)00114-3 

R. Alcalá, M. J. Gacto, F. Herrera, J. Alcalá-Fdez, A multi-objective genetic algorithm for tuning and rule selection to obtain accurate and compact linguistic fuzzy rule-based systems. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems 15:5 (2007) 539-557,  doi: 10.1109/TFUZZ.2010.2041008 

M. J. Gacto, R. Alcalá, F. Herrera, Adaptation and application of multi-objective evolutionary algorithms for rule reduction and parameter tuning of fuzzy rule-based systems. Soft Computing 13:5 (2009) 419-436,  doi: 10.1007/s00500-008-0359-z 

P. Pulkkinen, H. Koivisto, A Dynamically Constrained Multiobjective Genetic Fuzzy System for Regression Problems. IEEE Transactions on Fuzzy Systems 18:1 (2010) 161-177,  doi: 10.1109/TFUZZ.2009.2038712 

H. Ishibuchi, Y. Nojima, Analysis of interpretability-accuracy tradeoff of fuzzy systems by multiobjective fuzzy genetics-based machine learning International Journal of Approximate Reasoning 44:1 (2007) 4-31,  doi: 10.1016/j.ijar.2006.01.004 

M. Cococcioni, P. Ducange, B. Lazzerini, F. Marcelloni, A Pareto-based multi-objective evolutionary approach to the identification of mamdani fuzzy systems. Soft Computing 11 (2007) 1013-1031,  doi: 10.1007/s00500-007-0150-6 

R. Alcalá and P. Ducange, F. Herrera, B. Lazzerini, F. Marcelloni, A Multi-Objective Evolutionary Approach to Concurrently Learn Rule and Data Bases of Linguistic Fuzzy Rule-Based Systems. IEEE Transactions on Fuzzy Systems 17:5 (2009) 1106-1122,  doi: 10.1109/TFUZZ.2009.2023113 

M.J. Gacto, R. Alcalá, F. Herrera, Integration of an Index to Preserve the Semantic Interpretability in the Multi-Objective Evolutionary Rule Selection and Tuning of Linguistic Fuzzy Systems. IEEE Transactions on Fuzzy Systems 18:3 (2010) 515-531,  doi: 10.1109/TFUZZ.2010.2041008 

Open problems and further developments

We end this section by highlighting some problems related to MOEFSs that represent current challanges and are worth being investigated.

1) Performance evaluation of MOEFSs: Comparing different multiobjective optimization techniques is a difficult task, since the optimization result is a set of nondominated solutions rather than a single solution. Researchers generally agree on considering two informal criteria to assess the quality of a solution set: The distance of the approximated points from the true Pareto front should be minimized, and solutions should be equally distribute along the front. Additionally, the extent of the obtained nondominated front should be maximized. In the literature, several performance measures have already been proposed to consider these criteria and to evaluate the search capacity of algorithms. The following measures are widely used: attainment surfaces, hypervolume, epsilon dominance, etc. A drawback of these measures is that the quality difference between the obtained FRBSs remains unclear. Moreover, the Pareto front approximation is generated with respect to the training data, whereas the performance of the algorithm should be evaluated with respect to test data by applying a statistical analysis.

The following papers includes MOEFSs studies on performace evaluation:

R. Alcalá, P. Ducange, F. Herrera, B. Lazzerini, and F. Marcelloni A multiobjective evolutionary approach to concurrently learn rule and data bases of linguistic fuzzy-rule-based systems. IEEE Transactions on Fuzzy Systems 17:5 (2009) 1106-1122, doi: 10.1109/TFUZZ.2009.2023113 

M.J. Gacto, R. Alcalá and F. Herrera Integration of an Index to Preserve the Semantic Interpretability in the Multiobjective Evolutionary Rule Selection and Tuning of Linguistic Fuzzy Systems. IEEE Transactions on Fuzzy Systems 18:3 (2010) 515-531, doi: 10.1109/TFUZZ.2010.2041008 

2) Reliable interpretability measures: The definition of interpretability greatly affects the comprehensibility of an FRBS and researchers are still looking for reliable and widely accepted interpretability measures. This problem is mainly related to contributions of the first category.

The following paper discusses this problem in detail and proposes a taxonomy to organize the different measures or constraints that are used in the literature to assess interpretability in linguistic FRBSs.

M.J. Gacto, R. Alcalá and F. Herrera Interpretability of Linguistic Fuzzy Rule-Based Systems: An Overview of Interpretability Measures. Information Sciences 181:20 (2011) 4340-4360, doi: 10.1016/j.ins.2011.02.0212023113 

3) Objective dimensionality: MOEAs usually work very well for two or three objective problems, whereas their search capacity worsens as the number of objectives increases. Problems with four or more objectives are often called many-objective problems (H. Ishibuchi, N. Tsukamoto, and Y. Nojima (2004) Evolutionary many-objective optimization: A short review. IEEE Congress on Evolutionary Computation: 2419-2426, doi: 10.1109/CEC.2008.4631121). These kinds of problems can be handled by different approaches: 1) integrating many aspects into few objectives; 2) selecting few aspects as objectives; 3) using all the objectives. All these strategies present advantages and disadvantages. A possible solution is to realize a low selection pressure by inducing a preference ordering over the points in the nondominated set. The approaches that are based on preference ordering include relaxing the concept of Pareto dominance, controlling the dominance area, modifying the rank definition, substituting the distance metric, etc. These approaches seem promising, but they still need further investigation.

4) Scalability issues: In recent years, having to deal with large or high-dimensional datasets has become more common. Large datasets include many instances,while high-dimensional datasets refer to datasets with a large number of features. These kinds of datasets provide some difficulties: the size of large datasets affects the fitness function computation, thus increasing the computational time, whereas high-dimensional datasets increase the search space. Moreover, in most of the cases, the wider the search space, the greater the number of generated rules. Resulting models can be very complex, with interpretability heavily affected.

The following paper presents the application of a MOEFS to large and high-dimensional datasets:

R. Alcalá, M.J. Gacto, F. Herrera A Fast and Scalable Multiobjective Genetic Fuzzy System for Linguistic Fuzzy Modeling in High-Dimensional Regression Problems. IEEE Transactions on Fuzzy Systems 19:4 (2011) 666-681, doi: 10.1109/TFUZZ.2011.2131657 

5) Application to imbalanced datasets: Problems with imbalanced datasets appear mainly when dealing with classification tasks. Usually, the accuracy of a classifier is evaluated according to the percentage of correct classification, which should be maximized by the optimization process. This measure is inappropriate when the application domain is characterized by a highly imbalanced distribution of samples, since positive cases compose just a small fraction of the available data used to train the classifier. In some cases, the cost of misclassification is different between the positive and negative classes. Thus, the obtained classifier presents a high predictive accuracy over the majority class and poor predictive accuracy over the minority class. Furthermore, the minority class examples can be considered as noise and completely ignored. Two approaches can be followed to reduce or avoid bias toward the majority class. 1) At data level: Preprocessing mechanisms can be applied to patterns to prevent imbalance. 2) At algorithmic level: Solutions are mainly based on costsensitive approaches, by using metrics that take into account the misclassification costs of each class.

In the following paper, MOEFSs are applied to datasets characterized by highly imbalanced distributions of examples:

P. Ducange, B. Lazzerini, F. Marcelloni, Multi-Objective Genetic Fuzzy Classifiers for Imbalanced and Cost-Sensitive Datasets. Soft Computing 14:7 (2009) 713-728, doi: 10.1007/s00500-009-0460-y 

6) Automatic selection of the most suitable solution: The strength of MOEAs resides in their ability to approximate a wide part of the Pareto front, thus providing multiple solutions with different tradeoffs between objectives. However, in many application fields, only a single solution is required. The problem of automatically choosing a single solution for a specific purpose has not been discussed in the studies presented so far. Focusing on a set of obtained FRBSs (and on a single FRBS) represents a way to ease the choice of an appropriate single solution. However, this kind of visualization is a difficult task when the number of objectives increases, since it is impossible to show all the nondominated solutions in many-dimensional visualization spaces. The obtained FRBSs also present the problem of overfitting since they are evaluated according to test data (generalization ability). Since MOEFSs are expected to obtain a large set of FRBSs, the choice of a single solution should consider FRBSs with good generalization abilities. However, this is not an easy task since it has to be included in the learning process; therefore, it is only possible to take into account the results of the training set, while the test set remains unused.

7) Integration of decision maker's preferences: In a multiobjective optimization problem, exploring the whole search space can be unnecessary if the final goal is to find only those solutions that satisfy some requirements specified by the decision maker. A good strategy may be to direct the search process toward the areas of the Pareto front that better reflect the decision maker's preferences, by integrating these preferences into the optimization process. This way, the search space is reduced, and the efficiency of the search process is significantly increased. The incorporation of decision maker's preferences is an interesting research issue which has yet to be well explored in the literature.

The following paper proposes a method to take into account decision maker's preferences:

Y. Nojima and H. Ishibuchi, Incorporation of user preference into multiobjective genetic fuzzy rule selection for pattern classification problems. Artificial Life and Robotics 14 (2009) 418-421, doi: 10.1007/s10015-009-0700-3 

8) Design MOEFSs to generate type-2 fuzzy systems: At the end of the 1990s, a new class of fuzzy system was presented , in which the antecedent or consequent membership functions were type-2 fuzzy sets. The concept of a type-2 fuzzy set is introduced by Zadeh as a generalization of the concept of an ordinary fuzzy set, also referred to as type-1 fuzzy set. A type-2 fuzzy set incorporates uncertainty about the membership function into fuzzy set theory since its membership function is 3-D, where the third dimension is the value of the membership function at each point on its 2-D domain. If there is no uncertainty, a type-2 fuzzy set is reduced to a type-1 fuzzy set. Such sets are useful when it is difficult to determine an exact membership function for a fuzzy set. As in the case of type-1 fuzzy systems, the hybridization of type-2 fuzzy systems and GAs was proposed in order to automatically design type-2 fuzzy systems. Despite this, as far as we know, no proposals have yet been presented to combine MOEAs with type-2 fuzzy systems, therefore this may be a new and promising research field.

Slides for GFS presentations

R. Alcalá (July 2013) . FUZZ-IEEE 2013 Tutorial: Multi-Objective Evolutionary Fuzzy Systems: An Overview by Problem Objectives Nature and Optimized Components

The slides of this talk are associated to the FUZZ-IEEE 2013 Tutorial T4 (2013 IEEE International Conference on Fuzzy Systems, Hyderabad, India).

R. Alcalá (June 2011) . FUZZ-IEEE 2011 Tutorial: Evolutionary Multi-Objective Design of Fuzzy Rule-Based Systems

The slides of this talk are associated to the FUZZ-IEEE 2011 Tutorial T1 (2011 IEEE International Conference on Fuzzy Systems, Taipei, Taiwan).

F. Marcelloni (April 2011) . Multi-objective Evolutionary Learning of Fuzzy Rule-based Systems for Regression Problems

The slides of this talk are associated to the GEFS 2011 Plenary Talk from Professor Francesco Marcelloni (5th International Workshop on Genetic and Evolutionary Fuzzy Systems, Paris, France) which was held within the Symposium Series of Computational Intelligence, SSCI 2011.

H. Ishibuchi (November-December 2009) . Multiobjective Genetic Fuzzy Systems -Accurate and Interpretable Fuzzy Rule-Based Classifier Design

The slides of this talk are associated to the ISDA 2009 Plenary Talk from Professor Hisao Ishibuchi (9th International Conference on Intelligent Systems Design and Applications, Pisa, Italy).

H. Ishibuchi and R. Alcalá (August 2009) . Evolutionary Multi-Objective Design of Fuzzy Rule-Based Systems

The slides of this talk are associated to the FUZZ-IEEE 2009 Tutorial T1 (2009 IEEE International Conference on Fuzzy Systems, ICC Jeju, Jeju Island, Korea).

F. Herrera (March 2008) . Genetic Fuzzy Systems: Basic notions and Tuning Methods

The slides of this talk are associated to the paper: F. Herrera, Genetic Fuzzy Systems: Taxonomy, Current Research Trends and Prospects . Evolutionary Intelligence 1 (2008) 27-46 doi: 10.1007/s12065-007-0001-5 

J. Alcalá-Fdez et al. (March 2008) . KEEL: A Software Tool to Assess Evolutionary Algorithms for Data Mining Problems

The slides of this talk are associated to the contribution: J. Alcalá-Fdez, S. García, F.J. Berlanga, A. Fernández, L. Sánchez, M.J. del Jesus, F. Herrera, KEEL: A Data Mining Software Tool Integrating Genetic Fuzzy Systems . 3rd International Workshop on Genetic and Evolving Fuzzy Systems (GEFS 2008), Witten-Bommerholz (Germany), 83-88, 4-7 March 2008.

O. Cordón (July 2007) . Genetic Fuzzy Systems: Fuzzy Knowledge Extraction by Evolutionary Algorithms

The slides of this talk are associated to the I European Centre of SoftComputing (ESCS) Summer School.

H. Ishibuchi (July 2007) . Multiobjective Genetic Fuzzy Systems: Review and Future Research Directions

The slides of this talk are associated to the contribution: H. Ishibuchi, Multiobjective Genetic Fuzzy Systems: Review and Future Research Directions . Proc. of 2007 IEEE International Conference on Fuzzy Systems pp. 913-918, London, UK, July 23-26, 2007  

Software and Algorithm Implementations

Knowledge Extraction based on Evolutionary Learning (KEEL): KEEL is a software tool to assess evolutionary algorithms for Data Mining problems including regression, classification, clustering, pattern mining and so on. It contains a big collection of classical knowledge extraction algorithms, preprocessing techniques (instance selection, feature selection, discretization, imputation methods for missing values, etc.), Computational Intelligence based learning algorithms, including evolutionary rule learning algorithms based on different approaches (Pittsburgh, Michigan and IRL, ...), and hybrid models such as genetic fuzzy systems, evolutionary neural networks, etc. It allows us to perform a complete analysis of any learning model in comparison to existing ones, including a statistical test module for comparison. Moreover, KEEL has been designed with a double goal: research and educational. This software tool will be available as open source software this summer. For more information about this tool, please refer to the following publication:

 

J. Alcalá-Fdez, L. Sánchez, S. García, M.J. del Jesus, S. Ventura, J.M. Garrell, J. Otero, C. Romero, J. Bacardit, V.M. Rivas, J.C. Fernández, F. Herrera, Incorporation of user preference into multiobjective genetic fuzzy rule selection for pattern classification problems. Soft Computing, 13:3 (2009) 307-318. doi: 10.1007/s00500-008-0323-y  

KEEL Data Set Repository (KEEL-dataset): KEEL-dataset repository is devoted to the data sets in KEEL format which can be used with the software and provides: A detailed categorization of the considered data sets and a description of their characteristics. Tables for the data sets in each category have been also created; A descriptions of the papers which have used the partitions of data sets available in the KEEL-dataset repository. These descriptions include results tables, the algorithms used and additional material. For more information about this repository, please refer to the following publication:

 

J. Alcalá-Fdez, A. Fernández, J. Luengo, J. Derrac, S. García, L. Sánchez, F. Herrera, IKEEL Data-Mining Software Tool: Data Set Repository, Integration of Algorithms and Experimental Analysis Framework. Journal of Multiple-Valued Logic and Soft Computing 17:2-3 (2011) 255-287. 

Tackling New Problems with Genetic Fuzzy Systems

Here, we will present some novel areas that are worth being explored in the near future, and can provide interesting and promising results with GFS. Specifically, we describe the following problems:

1) Subgroup Discovery

2) Imbalanced Data-sets

3) Learning from Low Quality Data

4) Scalability of GFSs: High Dimensional and Large Scale Problems

GFSs for Subgroup discovery.

Subgroup discovery is a form of supervised inductive learning of subgroup descriptions in which, given a set of data and having a property of interest to the user, attempts to locate subgroups which are statistically "most interesting" for the user. Subgroup discovery has the objective of discovering interesting properties of subgroups obtaining simple rules (i.e. with an understandable structure and with few variables), highly significant and with high support (i.e. covering many of the instances of the target class). The concept was initially formulated by Klösgen in his rule learning algorithm EXPLORA (Klösgen W (1996) EXPLORA: a multipattern and multistrategy discovery assistant. In: Fayyad UM, Piatetsky-Shapiro G, Smyth P, and Uthurusamy R (Eds.), Advances in Knowledge Discovery and Data Mining, MIT Press, pp 249-271) and by Wrobel in the algorithm MIDOS (Wrobel S (1997) An algorithm for multi-relational discovery of subgroups. In: Proceedings of the First European Symposium on Principles of Data Mining and Knowledge Discovery (PKDD), Berlin, pp 78-87). Both use a rule-extraction model based on decision trees, in order to obtain the best subgroups among the population.

In order to evaluate the subgroups, evaluation measurements are defined which determine the interest of an expression through a combination of unusualness and size. MIDOS tackles, within this same approach, the problem of discovery in multi-relational databases. A recent study on the topic can be found in (Lavrac N , Cestnik B, Gamberger D, Flach P (2004) Decision support through subgroup discovery: three case studies and the lessons learned. Machine Learning 57:115-143, doi: 10.1023/B:MACH.0000035474.48771.cd).

The following papers includes GFSs studies for Subgroup Discovery:

M.J. del Jesus, P. González, F. Herrera, M. Mesonero Evolutionary fuzzy rule induction process for subgroup discovery: A case study in marketing. IEEE Transactions on Fuzzy Systems 15:4 (2007) 578-592, doi: 10.1109/TFUZZ.2006.890662 

C. Romero, P. González, S. Ventura, M.J. del Jesus, F. Herrera E, Evolutionary algorithms for subgroup discovery in e-learning: A practical application using Moodle data. Expert Systems With Applications 36 (2009) 1632-1644 , doi: 10.1016/j.eswa.2007.11.026 

GFSs for Classification with Imbalanced Data-Sets.

The treatment of data-sets with imbalanced classes is one of the emerging issues in the field of machine learning, specially when we face applications of different domains (Chawla N, Japkowicz N, Kolcz A (2004) Editorial: special issue on learning from imbalanced data sets. SIGKDD Explorations 6:1 1-6. and Batista GEAPA, Prati RC, Monard MC (2004) A study of the behaviour of several methods for balancing machine learning training data. SIGKDD Explorations 6:1 20-29) The presence of classes with few data can generate sub-optimal classification models, since there is a bias towards the majority class, as the rules that predicts the higher number of examples are positively weighted during the learning process in favour of the accuracy metric (Japkowicz N, Stephen S (2002) The class imbalance problem: a systematic study (2002) Intelligent Data Analysis 6:5 429-450). The particularities associated with these problems require the adaptation of the existing Fuzzy Rule Basde Classification Systems (FRBCSs) algorithms and the design of new models where the GFSs could adapt to this type of classes, together with specific metrics in the fitness function, multiple objectives measuring the performance on each of the classes, approaches for multi-class problems (more than 2 classes) etc. The following papers are three first studies on the use of FRBCSs for imbalanced data sets. The first ones are fuzzy rule learning proposals, one is based on costs (L. Xu, M. Chow, L. Taylor, Power distribution fault cause identification with imbalanced data using the data mining-based fuzzy classification e-algorithm, IEEE Trans. Power Systems 22:1 (2007) 164-171, doi: 10.1109/TPWRS.2006.888990) and the other one employs Granular Computing which builds Information Granules according to the class distribution (M.-C. Chen, L.-S. Chen, C.-C. Hsu, W.-R. Zeng, An information granulation based data mining approach for classifying imbalanced data, Information Sciences 178:16 (2008) 3214-3227, doi: 10.1016/j.ins.2008.03.018 ). The last study presents and analysis on the best configuration of the fuzzy components and the synergy with preprocessing techniques to deal with the problem of imbalanced data-sets (A. Fernández, S. García, M.J. del Jesus, F. Herrera, A study of the behaviour of linguistic fuzzy rule based classification systems in the framework of imbalanced data-sets. Fuzzy Sets and Systems, 159:18 (2008) 2378-2398, doi: 10.1016/j.fss.2007.12.023).

Regarding GFSs, some recent papers that use a genetic tuning for FRBCSs in order to improve the behaviour of FRBCSs in the framework of imbalanced data-sets can be found in:

Regarding GFSs, some recent papers that use a genetic tuning for FRBCSs in order to improve the behaviour of FRBCSs in the framework of imbalanced data-sets can be found in:

A. Fernández, M.J. del Jesus, F. Herrera, Hierarchical Fuzzy Rule Based Classification Systems with Genetic Rule Selection for Imbalanced Data-Sets. International Journal of Approximate Reasoning 50 (2009) 561-577, doi: 10.1016/j.ijar.2008.11.004 

A. Fernández, M.J. del Jesus, F. Herrera, On the Influence of an Adaptive Inference System in Fuzzy Rule Based Classification Systems for Imbalanced Data-Sets. Expert Systems With Applications 36:6 (2009) 9805-9812,   doi: 10.1016/j.eswa.2009.02.048 

P. Ducange, B. Lazzerini, F. Marcelloni, Multi-Objective Genetic Fuzzy Classifiers for Imbalanced and Cost-Sensitive Datasets. Soft Computing 14:7 (2009) 713-728,   doi: 10.1007/s00500-009-0460-y 

A. Fernández, M.J. del Jesus, F. Herrera, On the 2-Tuples Based Genetic Tuning Performance for Fuzzy Rule Based Classification Systems in Imbalanced Data-Sets. Information Sciences 180:8 (2010) 1268-1291,   doi: 10.1016/j.ins.2009.12.014 

GFSs for Learning from Low Quality Data.

There are many practical problems requiring learning models from uncertain data. The experimental designs of GFSs learning from data observed in an imprecise way are not being actively studied by researchers. However, according to the point of view of fuzzy statistics, the primary use of fuzzy sets in classification and modelling problems is for the treatment of vague data. Using vague data to train and test GFSs we could analyze the performance of these classifiers on the type of problems for which fuzzy systems are expected to be superior. Preliminary results in this area involve the proposals of different formalizations for the definition of fuzzy classifiers, based on the relationships between random sets and fuzzy sets (Sánchez L, Casillas J, Cordón O, del Jesus MJ (2001) Some relationships between fuzzy and random set-based classifiers and models. International Journal of Approximate Reasoning 29:2 (2001) 175-213, doi: 10.1016/S0888-613X(01)00063-9).

This is a novel area that is worth being explored in the near future, and can provide interesting and promising results. The following papers tackle the use of GFSs with low quality data:

L. Sánchez, I. Couso Advocating the use of imprecisely observed data in genetic fuzzy systems. IEEE Transactions on Fuzzy Systems 15:4 (2007) 551-562, doi: 10.1109/TFUZZ.2007.895942 

L. Sánchez, M.R. Suárez, J.R. Villar, I. Couso Mutual information-based feature selection and partition design in fuzzy rule-based classifiers from vague data. International Journal of Approximate Reasoning 49:3 (2008) 607-622, doi: 10.1016/j.ijar.2008.06.005 

L. Sánchez, J. Otero, I. Couso Obtaining Linguistic Fuzzy Rule-based Regression Models from Imprecise Data with Multiobjective Genetic Algorithms. Soft Computing 13:5 (2009) 467-479, doi: 10.1007/s00500-008-0362-4 

L. Sánchez, I. Couso, J. Casillas Genetic learning of fuzzy rules based on low quality data. Fuzzy Sets and Systems 160:17 (2009) 2524-2552, doi: 10.1016/j.fss.2009.03.004 

L. Sánchez, I. Couso Obtaining Fuzzy Rules from Interval Censored Data with Genetic Algorithms and a Random Sets-based Semantic of the Linguistic Labels. Soft Computing 15:10 (2011) 1945-1957, doi: 10.1007/s00500-010-0627-6 

A. Palacios, L. Sánchez, I. Couso Future performance modeling in athletism with low quality data-based GFSs. Journal of Multiple-Valued Logic and Soft Computing 17:2-3 (2011) 207-228.  

Scalability of GFSs: High Dimensional and Large Scale Problems.

Linguistic fuzzy modeling in high-dimensional and large scale datasets is a challenging topic since conventional linguistic Fuzzy Rule-Based Systems (FRBSs) suffer from exponential rule explosion when the number of variables and/or data examples becomes high (see W.E. Combs, J.E. Andrews (1998) Combinatorial rule explosion eliminated by a fuzzy rule configuration. IEEE Trans. Fuzzy Syst. 6(1):1-11 and Y. Jin (2000) Fuzzy modeling of high-dimensional systems: Complexity reduction and interpretability improvement. IEEE Trans. Fuzzy Syst. 8(2):212-221). Another problem when we deal with high-dimensional datasets is the analysis of algorithm scalability on big databases, emphasizing the training time and the convergence towards compact and interpretable models (F. Herrera (2008) Genetic fuzzy systems: taxonomy, current research trends and prospects. Evolutionary Intelligence 1:27-46). In this way, we can distinguish two kinds of problems, which should be solved by applying different kinds of techniques but both together:

1) High dimensional problems: When a large number of variables have to be considered.

2) Large scale datasets: When dealing with datasets comprised of a large amount of data.

A good way to address both problems is by searching for a good and simple global structure within the same process, in order to consider the relationships among the different components defining the Knowledge Base of the obtained linguistic models. Since this method involves using different coding schemes to represent each solution, GFSs become an useful tool for this task. However, this method involves a lot of components/parameters that should be determined together: selection of important variables, determination of a good number of linguistic terms or granularities per variable, parametric definition of the membership functions and associated set of rules. Since evolutionary algorithms are computationally expensive techniques and this involves using different coding schemes to represent a complete solution and therefore a very complex search space, this is a difficult task. In fact, the balance among problem size, algorithm scalability and solution quality is an important topic for GFSs that is worth studying in depth (F. Herrera (2008) Genetic fuzzy systems: taxonomy, current research trends and prospects. Evolutionary Intelligence 1:27-46), which has not been directly taken into account in most of the evolutionary approaches devoted to linguistic fuzzy modelling.

In the following, we can find some significant and/or recent papers addressing both high dimensional and large scale problems by using GFSs. They are: a first paper devoted to regression problems tackling high dimensionality and large scale datasets, and a second paper devoted to classification problems particularly tackling high dimensionality:

R. Alcalá, M. J. Gacto, F. Herrera, A Fast and Scalable Multiobjective Genetic Fuzzy System for Linguistic Fuzzy Modeling in High-Dimensional Regression Problems. IEEE Transactions on Fuzzy Systems 19:4 (2011) 666-681,   doi: 10.1109/TFUZZ.2011.2131657    COMPLEMENTARY MATERIAL to the paper here: dataset partitions, results, figures, etc.

J. Alcalá-Fdez, R. Alcalá, F. Herrera, A Fuzzy Association Rule-Based Classification Model for High-Dimensional Problems with Genetic Rule Selection and Lateral Tuning. IEEE Transactions on Fuzzy Systems 19:5 (2011) 857-872,   doi: 10.1109/TFUZZ.2011.2147794 

Recent Journal Papers on Genetic Fuzzy Rule Based Systems (2007-Present)

We have performed a bibliography compilation of journal papers on Genetic Fuzzy Rule Based Systems (from 2007 to present). It is maintained by R. Alcalá and M. J. Gacto.

If you would like to include or correct any of the references on this page, please contact the maintainer in his/her e-mail address: alcala@decsai.ugr.es or mgacto@ujaen.es

Related Review Papers and Websites

Since the types and application domains of GFSs are quite extense, there exist many highly related topics. This section includes some related review papers and Websites that, because of their importance within the GFS framework, should be taken into account as additional bibliographic materials.

Related Review Papers.

In the following we maintain a list with new related papers reviewing particular GFS types or important application domains:

Interpretability Measures for Linguistic FRBSs (including descriptions of measures)
Gacto M.J., Alcalá R., Herrera F. , Interpretability of Linguistic Fuzzy Rule-Based Systems: An Overview of Interpretability Measures. Information Sciences 181:20 (2011) 4340-4360,   doi: 10.1016/j.ins.2011.02.021    COMPLEMENTARY MATERIAL to the paper here: links to the papers with doi, new contributions, etc.

Mamdani-type GFSs
Cordón O. , A Historical Review of Evolutionary Learning Methods for Mamdani-type Fuzzy Rule-based Systems: Designing Interpretable Genetic Fuzzy Systems. International Journal of Approximate Reasoning 52:6 (2011) 894-913,   doi: 10.1016/j.ijar.2011.03.004 

Related Websites.

Here we maintain a list of related websites including topics of interest within the GFS framework:

• Interpretability of Linguistic Fuzzy Rule-Based Systems

This website contains materials related to interpretability of Linguistic FRBSs which is an important topic within GFSs due to their flexibility to consider both accuracy and interpretability of FRBSs together. For example by fitness aggregation or by using MOEAs.

• Statistical Inference in Computational Intelligence and Data Mining

This website contains materials related to the use of statistical tests for pair-wise and multiple comparisons among different methods. This is essential a well knowledge and use of these kinds of techniques in order to state well supported conclusions by properly assessing the superior quality of the new proposed GFSs.

Future Events

Special Session - Evolutionary Fuzzy Systems (Session webpage)

Organizers: Yusuke Nojima, Rafael Alcalá, Hisao Ishibuchi
This session has been accepted at the FUZZ-IEEE 2017 conference which will be held in Naples, Italy at July 9-12, 2017.

Information on Past Events can be found here.

 

(This Web page was created and maintained by Alberto Fernández Hilario, María José Gacto and Rafael Alcalá)