CW (L. Zadeh. Fuzzy logic = computing with words. IEEE Transactions on Fuzzy Systems, 4(2):103-111, 1996 doi: 10.1109/91.493904) deals with words and propositions from a natural language as the main objects of computation, for example: "small", "big", "expensive", "quite possible" or even more complex sentences as "tomorrow will be cloudy but not very cold". The main inspiration of CW is the human ability of performing several different tasks (walk in the street, play football, ride a bicycle, understand a conversation, making a decision...) without needing an explicit use of any measurements nor computations. This capability is sustained by the brain's ability to manipulate different perceptions (usually imprecise, uncertain or partial perceptions), which plays a key role in human recognition, decision and execution processes.

CW is a methodology which contrasts with the usual sense of Computing, that is, manipulating numbers and symbols. Therefore, CW provides a methodology which can bring closer the gap between human's brain mechanisms and the machine's processes to solve problems providing computers with tools to deal with imprecision, uncertainty and partial truth.

Decision Making (T. Evangelos. Multi-criteria decision making methods: a comparative study. Kluwer Academic Publishers, Dordrecht, 2000) can be seen as the final outcome of some mental processes that lead to the selection of an alternative among several different ones. For example, typical decision making problems are to choose the best car to buy, deciding which candidate is more suitable for a certain position in a firm or choosing the most appropriate clothes for a meeting. It is interesting to note that decision making is an inherent human ability which is not necessarily rationally guided, which can be based on explicit or tacit assumptions and that it does not need precise and complete measurements and information about the set of feasible alternatives. This fact has led to many authors to apply fuzzy sets theory (L. Zadeh. Fuzzy sets. Information and Control, 8:338-353, 1965 doi: 10.1016/S0019-9958(65)90241-X) to model the uncertainty and vagueness in decision processes.

In recent years, many researchers have seen CW as a very interesting methodology to be applied in decision making (F. Herrera, E. Herrera-Viedma. Linguistic Decision Analysis: Steps for Solving Decision Problems under Linguistic Information. Fuzzy Sets and Systems 115 (2000) 67-82 doi: 10.1016/S0165-0114(99)00024-X). As it allows to model perceptions and preferences in a more human like style and it can provide computers some of the needed tools, if not to fully simulate human decision making, to develop complex decision support systems to ease the decision makers to reach a solution.

A Bird's Eye View on CW

CW, that is, the methodology that uses words and propositions from a natural language as its main objects of computation, was introduced by L. Zadeh in the seminal paper (L. Zadeh. Outline of a new approach to the analysis of complex systems and decision processes. IEEE Transactions on Systems, Man and Cybernetics, SMC-3(1):28-44, 1973 ). In that paper, the main concepts of CW were presented: granules and linguistic variables.

According to Zadeh (L. Zadeh. Toward a theory of fuzzy information granulation and its centrality in human reasonning and fuzzy logic. Fuzzy Sets and Systems, 90:111-127, 1997 doi:10.1016/S0165-0114(97)00077-8):

A granule is "a clump of objects (or points) which are drawn together by indistinguishability, similarity, proximity or functionality".

In the next figure we can see an example of granulation where the granules of a personal computer are the computer case, the screen, the keyboard and the mouse. Additionally, the granules of the computer case are the CPU, the motherboard, the main memory, the hard disk and the expansion cards. We can notice that granulation, that is, the decomposition of whole into parts is, in general, hierarchical in nature.

 

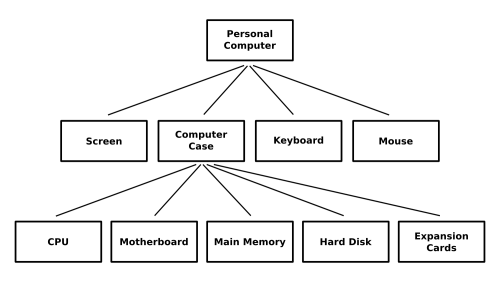
Granules can be seen from fuzzy perspective in those processes that deal with human reasoning and concept formation. Following the above example, it is not difficult to find personal computers in which the computer case is integrated in the screen device or motherboards that incorporate several expansion cards (graphical and sound devices) making difficult to differentiate the granules and extending their meaning in an unclear and uncertain way. Moreover, the granules are usually associated with fuzzy attributes, e.g., it is possible to classify storage devices according to the attribute "storage capacity" with the fuzzy values "large", "medium" or "low". This fuzziness of granules, their attributes and their values is charactersitic of the ways in which human concepts are formed, organized and manipulated.

The concept of fuzzy granulation has been extensively studied in the literature:

(T.D. Pham. Computing with words in formal methods. International Journal of Intelligent Systems, 15(8):801-810, 2000 doi:10.1002/1098-111X(200008)15:8<801::AID-INT7>3.0.CO;2-Z) discusses how fuzzy information granulation theory can be used as a base to build flexible formal software specifications. (A. Bargiela and W. Pedrycz. Granular mappings. IEEE Transactions on Systems, Man, and Cybernetics Part A: Systems and Humans, 35(2):292-297, 2005 doi:10.1109/TSMCA.2005.843381) study granular mappings for both set and fuzzy set based granulation. (S. Dick, A. Schenker, W. Pedrycz, and A. Kandel. Regranulation: A granular algorithm enabling communication between granular worlds. Information Sciences, 177(2):408-435, 2007 doi:10.1016/j.ins.2006.03.020) present a granular algorithm to translate information between two different granular worlds with different granulations.

Another basic assumption in CW is that information is conveyed by constraining the value of variables. Moreover, the information is assumed to consist of a collection of propositions expressed in a natural or synthetic language, that is, variables take as possible values linguistic ones. To manage linguistic information Zadeh introduced linguistic variables ( L. Zadeh. The concept of a linguistic variable and its application to approximate reasoning. part I. Information Sciences, 8(3):199-249, 1975 doi:10.1016/0020-0255(75)90036-5):

A linguistic variable is a "variable whose values are not numbers but words or sentences in a natural or artificial language".

The main purpose of using linguistic values (words or sentences) instead of numbers is that linguistic characterizations are, in general, less specific than numerical ones, but much more closer to the way that humans express and use their knowledge. For example, if we say "the building is tall" is less specific than "the building measures 300 meters". In that case, "tall" can be seen as a linguistic value of the variable "height" which is less precise and informative than the numerical value "300". Despite its less informative nature, the value "tall" allows humans to naturally express and deal with information that may be uncertain or incomplete (the speaker may not know the exact building height). As this kind of situations where information is not precise are very common in real life, linguistic variables can be a powerful tool to model human knowledge.

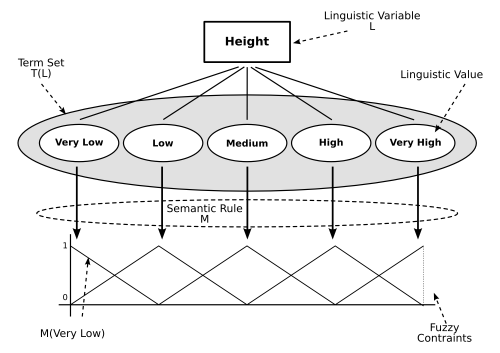
In the next figure we can see an example of the linguistic variable "Height", whose correspondig linguistic term set is T(Height)={Very Low, Low, Medium, High, Very High}. It is clear that a crucial aspect that will determine the validity of a CW approach is the determination of correct membership functions for the linguistic term set.

Perceptual Computer

Additionally, the following papers by Trillas et al. and Mendel have described in more detail the tight relationship between fuzzy sets theory and CW and how CW can be used to transcend the current computation schemes that deal with measurements to a new kind of computing where data takes form of perceptions (thus arising the concept of perceptual computer as an architecture for the CW methodology):

• E. Trillas. On the use of words and fuzzy sets. Information Sciences, 176(11):1463-1487, 2006 doi:10.1016/j.ins.2005.03.008
• E. Trillas and S. Guadarrama. What about fuzzy logic's linguistic sound- ness? Fuzzy Sets and Systems, 156(3):334-340, 2005 doi:10.1016/j.fss.2005.05.028
• J.M. Mendel. Computing with words and its relationships with fuzzistics. Information Sciences, 177(4):988-1006, 2007 doi:10.1016/j.ins.2006.06.008
• J.M. Mendel. The perceptual computer: An architecture for computing with words. In IEEE International Conference on Fuzzy Systems, volume 1, pages 35-38, 2001 doi:10.1109/FUZZ.2001.1007239
• J.M. Mendel. An architecture for making judgement using computing with words. International Journal of Applied Mathematics and Computer Sciences, 12(3):325-335, 2002.
• D. Wu and J.M. Mendel. Perceptual reasoning using interval type-2 fuzzy sets: Properties. IEEE International Conference on Fuzzy Systems, pages 1219-1226, 2008 doi:10.1109/FUZZY.2008.4630526

 

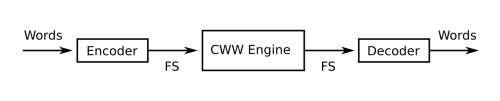
In the next figure a diagram of a perceptual computer is shown: An Encoder transforms linguistic perceptions into fuzzy sets and leads to a codebook of words with their associated fuzzy sets. The outputs of the Encoder activate a CWW Engine, whose output is another fuzzy set, which is then mapped by a Decoder into a word most similar to a codebook word. The origins of perceptual computing can be tracked to (R.M. Tong and P.P. Bonissone. A linguistic approach to decisionmaking with fuzzy sets. IEEE Transactions on Systems, Man and Cybernetics, SMC-10(11):716-723, 1980 doi:10.1109/TSMC.1980.4308391). Moreover, Schmucker in his monography (K.S. Schmucker. Fuzzy Sets, Natural Language Computations, and Risk Analysis. Computer Science Press, Rockville, MD, 1984) presented the essence of perceptual computing.

Another important concept is the retranslation process in CW, that is, to approximately describe a given fuzzy set in natural language. Yager studied this problem (R.R. Yager. On the retranslation process in zadeh's paradigm of computing with words. IEEE Transactions on Systems, Man, and Cybernetics - Part B: Cybernetics, 34(2):1184-1195, 2004 doi:10.1109/TSMCB.2003.821866) and Martin et al. presented two new different approaches to deal with this retranslation problem in the computing with perceptions field (O. Martin and G.J. Klir. On the problem of retranslation in computing with perceptions. International Journal of General Systems, 35(6):655-674, 2006 doi:10.1080/03081070600861123).

Approaches and Methodologies for CW

The high attention that CW has received in the last years can be noted from the publication of several new different approaches and methodologies for CW:

Lawry presents both an alternative approach to CW based on mass assigment theory and a new framework for linguistic modelling that avoid some of the complexity problems that arise by the use of the extension principle in Zadeh's CW methodology: (J. Lawry. An alternative approach to computing with words. International Journal of Uncertainty, Fuzziness and Knowlege-Based Systems, 9 (Suppl):3-16, 2001 doi:10.1142/S0218488501000958, J. Lawry. A methodology for computing with words. International Journal of Approximate Reasoning, 28:51-89, 2001 doi:10.1016/S0888-613X(01)00042-1, J. Lawry. A framework for linguistic modelling. Artificial Intelligence, 155(1-2):1-39, 2004 doi:10.1016/j.artint.2003.10.001).

Rubin defines CW as a symbolic generalization of fuzzy logic (S.H. Rubin. Computing with words. IEEE Transactions on Systems, Man and Cybernetics, Part B: Cybernetics, 29(4):518-524, 1999 doi:10.1109/3477.775267)

Ying et al. propose a new formal model for CW based on fuzzy automatas whose inputs are strings of fuzzy subsets of the input alphabet (Y. Cao, M. Ying, and G. Chen. Retraction and generalized extension of computing with words. IEEE Transactions on Fuzzy Systems, 15(6):1238-1250, 2007 doi:10.1109/TFUZZ.2007.896301, M. Ying. A formal model of computing with words. IEEE Transactions on Fuzzy Systems, 10(5):640-652, 2002 doi:10.1109/TFUZZ.2002.803497)

Wang et al. extend Ying's work considering CW via a different computational model, in particular, Turing machines (H. Wang and D. Qiu. Computing with words via turing machines: A formal approach. IEEE Transactions on Fuzzy Systems, 11(6):742-753, 2003 doi:10.1109/TFUZZ.2003.819841)

Tang et al. present a new linguistic modelling that can be applied in CW which does not directly rely on fuzzy sets to model the meaning of natural language terms but uses some fuzzy relations between the linguistic labels to model their semantics (Y. Tang and J. Zheng. Linguistic modelling based on semantic similarity relation among linguistic labels. Fuzzy Sets and Systems, 157(12):1662-1673, 2006 doi:10.1016/j.fss.2006.02.014)

Türksen proposes the use of meta-linguistic axioms as a foundation for CW as an extension of fuzzy sets and logic theory (I.B. Turksen. Type 2 representation and reasoning for cww. Fuzzy Sets and Systems, 127:17-36, 2002 doi:10.1016/S0165-0114(01)00150-6)

At this point we center our attention in the work of Dubois and Prade (D. Dubois and H. Prade. The three semantics of fuzzy sets. Fuzzy Sets and Systems, 90:141-150, 1997 doi:10.1016/S0165-0114(97)00080-8) where they discuss and analyze the semantics of fuzzy sets. They say (page 141):

"Three main semantics for membership functions seem to exist in the literature: similarity, preference and uncertainty."

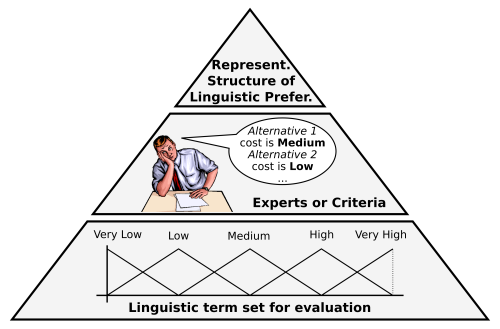
It is natural to think that the preference semantics of fuzzy sets is used in decision making: a particular preference of a decision maker can be expressed by using fuzzy preferences or linguistic labels. In the next figure we present a scheme of preference expression in a typical Linguistic Decision Making environment: first, a set of linguistic terms is defined, which is then used by the expert to provide his preferences. Those preferences will be finally represented using a particular representation structure of linguistic preferences (for example, linguistic utility functions or linguistic preference relations).

 

CW in Decision Making

In this section we center our attention into the application of the CW methodology in decision making:

• Steps for Solving Decision Making Problems under Linguistic Information: The Necessity of Aggregation
• Computational Models for CW in Decision Making

Steps for Solving Decision Making Problems under Linguistic Information: The Necessity of Aggregation

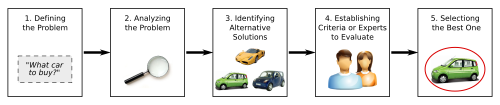
Prior to the resolution of any decision making problem, several steps must be followed:

• Defining the problem
• Analyzing the problem
• Identifying alternative solutions
• Establishing criteria or experts by which they can be evaluated
• Selecting the best one

In the next figure we see an example of those steps. First, the problem of choosing a car is defined. The second step is to analyze the problem: finding the real necessities of a car, discarding other types of vehicles, making a preliminary list of possible models and so on. On the third step, after the initial analysis of the problem, three particular cars have been selected as the possible solution alternatives. On the fourth step two different experts have been chosen to provide their preferences about the alternatives. Finally, on the last step, the decision process has been carried out and the best alternative has been selected.

 

In classical fuzzy decision analysis, the last step of a multi-criteria or group decision making process basically consists of two different phases (M. Roubens. Fuzzy sets and decision analysis. Fuzzy Sets and Systems, 90:199-206, 1997 doi: 10.1016/S0165-0114(97)00087-0):

An aggregation phase of the performance values with respect to all the criteria or decision makers to obtain a collective performance value for the alternatives.

An exploitation phase of the collective performance value to obtain a rank ordering, sorting or choice among the alternatives.

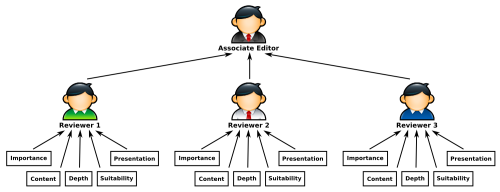
We can find a clear example of the application of the aggregation and exploitation phases in (W. Dongrui and J.M. Mendel. Aggregation using the linguistic weighted average and interval type-2 fuzzy sets. IEEE Transactions on Fuzzy Systems, 15(6):1145-1161, 2007 doi:10.1109/TFUZZ.2007.896325) where a decision process about the evaluation scheme for a journal is presented (see the next figure): The associate editor asks some reviewers (the decision makers) to review a particular paper for a journal and to choose about several different alternatives, for example: to reject it, to accept it if the authors improve the paper or to directly accept it as is. To evaluate and give their final decision on the paper, the reviewers must summarize and aggregate different criteria about the paper as importance, content, depth, presentation, suitability for the journal and so on. Once all the reviewers finish their evaluations the editor must summarize (aggregate) again all the information received from the reviewers and must apply an exploitation phase in which from the aggregated information the final evaluation for the paper is chosen (to reject, to resubmit or to accept it).

In (F. Herrera, E. Herrera-Viedma. Linguistic Decision Analysis: Steps for Solving Decision Problems under Linguistic Information. Fuzzy Sets and Systems 115 (2000) 67-82 doi: 10.1016/S0165-0114(99)00024-X), Herrera et al. analyze how in linguistic decision analysis it is necessary to introduce 2 prior steps before applying both the aggregation and exploitation phases, obtaining a three step solution scheme:

1. The choice of the linguistic term set with its semantics. It consists of establishing the linguistic expression domain used to provide the linguistic performance values about alternatives according to the different criteria. To do so, we have to choose the granularity of the linguistic term set, its labels and its semantics.
2. The choice of the aggregation operator of linguistic information. It consists of establishing an appropriate aggregation operator of linguistic information for aggregating and combining the linguistic performance values provided.
3. The choice of the best alternatives. It consists of choosing the best alternatives according to the linguistic performance values provided. It is carried out in two phases:
   1. Aggregation phase of linguistic information: It consists of obtaining a collective linguistic performance value on the alternatives by aggregating the linguistic performance values provided according to all the criteria / decision makers by means of the chosen aggregation operator of linguistic information.
   2. Exploitation phase: It consists of establishing a rank ordering among the alternatives according to the collective linguistic performance value for choosing the best alternatives.

From this three step solution scheme, it is clear that it is necessary to develop linguistic computational models that allow the representation and the aggregation of linguistic information, respectively.

Computational Models for CW in Decision Making

In the following we present the main computational models for linguistic aggregation that have been deployed in the decision making field:

• Linguistic Computational Model Based on Membership Functions
• Linguistic Computational Model Based on Type-2 Fuzzy Sets
• Linguistic Symbolic Computational Models Based on Ordinal Scales
• 2-tuple Linguistic Computational Model: A Symbolic Model Extending the Use of Indexes

Linguistic Computational Model Based on Membership Functions

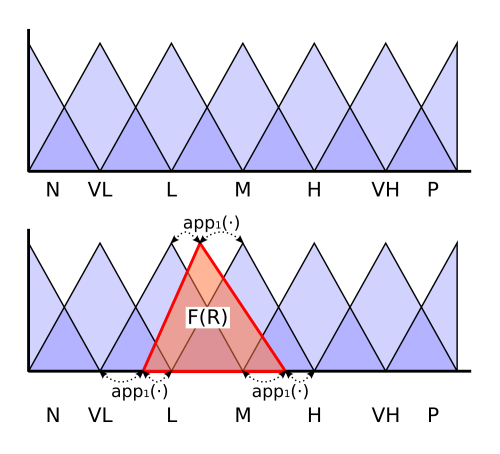
This computational model makes use of the Extension Principle from fuzzy arithmetic (R. Degani and G. Bortolan. The problem of linguistic approximation in clinical decision making. International Journal of Approximate Reasoning, 2:143-162, 1988 doi:10.1016/0888-613X(88)90105-3): the result of an aggregation function &Ftilde; over a set of n linguistic labels in the term set T(L) is a fuzzy number F(R) that usually does not have an associated linguistic label on T(L). Therefore, it is necessary to apply an approximation function app1(.) to associate it to a particular label on T(L) [the retranslation problem (O. Martin and G.J. Klir. On the problem of retranslation in computing with perceptions. International Journal of General Systems, 35(6):655-674, 2006 doi:10.1080/03081070600861123, R.R. Yager. On the retranslation process in zadeh's paradigm of computing with words. IEEE Transactions on Systems, Man, and Cybernetics - Part B: Cybernetics, 34(2):1184-1195, 2004 doi:10.1109/TSMCB.2003.821866)] or to use fuzzy ranking procedures to obtain a final order of the alternatives:

$$T(N)^n \xrightarrow{\;\; F \;\; } F(R) \xrightarrow{\;\; app_1(·) \;\; } T(L)$$

An example of the retranslation problem is presented in the next figure: Suppose that, as a result of the application of an aggregation function &Ftilde; we obtain a fuzzy number F(R) (in red in the figure) which does not have an associated linguistic label on a particular term set S={N,VL,L,M,H,VH,P}. To solve the problem we need an approximation function app1(.) that will assign one of the L or M labels to F(R). From the example, it is clear that the use of the approximation function to solve the retranslation problem introduces some loss of information which is a critical aspect to be taken into account in decision models.

In this model the aggregation is carried out directly acting over the membership functions associated to the linguistic labels using classical fuzzy arithmetic and obtaining a fuzzy set that represent the aggregated value. These approaches usually use ranking functions to order the fuzzy numbers and to obtain a final numerical evaluation (K. Anagnostopoulos, H. Doukas, and J. Psarras. A linguistic multicriteria analysis system combining fuzzy sets theory, ideal and anti-ideal points for location site selection. Expert Systems with Applications, 35(4):2041-2048, 2008 doi:10.1016/j.eswa.2007.08.074, G. Fu. A fuzzy optimization method for multicriteria decision making: An application to reservoir flood control operation. Expert Systems with Applications, 34(1):145-149, 2008 doi:10.1016/j.eswa.2006.08.021).

Linguistic Computational Model Based on Type-2 Fuzzy Sets

This computational model makes use of type-2 fuzzy sets to model linguistic assessments:

• J.M. Mendel. An architecture for making judgement using computing with words. International Journal of Applied Mathematics and Computer Sciences, 12(3):325-335, 2002
• J.M. Mendel. Historical reflections on perceptual computing. In Proceedings of the 8th International FLINS Conference on Computational Intelligence in Decision and Control, pages 181-186, 2008
• I.B. Türksen. Type 2 representation and reasoning for cww. Fuzzy Sets and Systems, 127:17-36, 2002 doi:10.1016/S0165-0114(01)00150-6
• I.B. Türksen. Meta-linguistic axioms as a foundation for computing with words. Information Sciences, 177(2):332-359, 2007 doi:10.1016/j.ins.2006.03.002

Some of the reasons for using type-2 fuzzy sets are:

• From (I.B. Türksen. Type 2 representation and reasoning for cww. Fuzzy Sets and Systems, 127:17-36, 2002 doi:10.1016/S0165-0114(01)00150-6):

"Type-1 representation is a `reductionist' approach for it discards the spread of membership values by averaging or curve fitting techniques and hence, camouflages the `uncertainty' embedded in the spread of membership values. Therefore, Type-1 representation does not provide good approximation to meaning representation of words and does not allow computing with words a richer platform."

• From (J.M. Mendel. Computing with words and its relationships with fuzzistics. Information Sciences, 177(4):988-1006, 2007 doi:10.1016/j.ins.2006.06.008):

"Words mean different things to different people and so are uncertain. We therefore need a fuzzy set model for a word that has the potential to capture its uncertainties, and an interval type-2 fuzzy set should be used as a fuzzy set model of a word."

The majority of the contributions in the field use interval type-2 fuzzy sets (a particular kind of type-2 fuzzy sets) which maintain the uncertainty modelling properties of general type-2 fuzzy sets but reduce the computational efforts that are needed to aggregate them. In (W. Dongrui and J.M. Mendel. Aggregation using the linguistic weighted average and interval type-2 fuzzy sets. IEEE Transactions on Fuzzy Systems, 15(6):1145-1161, 2007 doi:10.1109/TFUZZ.2007.896325) the Linguistic Weighted Average operator is presented. It can be seen as an extension of the Fuzzy Weighted Aggregation operator where both weights and attributes are words modelled by interval type-2 fuzzy sets.

It is worth to note that as the previous linguistic model, this type-2 fuzzy sets based model also suffers from the retranslation problem, that is, the resulting type-2 fuzzy set from an aggregation operation must be mapped into a linguistic assessment at the end of a decision process.

Linguistic Symbolic Computational Models Based on Ordinal Scales

In the literature, we can find 3 different linguistic symbolic computational models which are based on ordinal scales:

A linguistic symbolic computational model based on ordinal scales and max-min operators

A linguistic symbolic computational model based on indexes and

A linguistic symbolic computational model based on continuous term sets.

Linguistic symbolic computational model based on ordinal scales and max-min operators (R.R. Yager. A new methodology for ordinal multiobjective decisions based on fuzzy sets. Decision Sciences, 12(4):589-600, 1981 doi: 10.1111/j.1540-5915.1981.tb00111.x). It uses an ordered linguistic scale $S={s_1,...,s_g}$ with a linear ordering as the only structure available in S.

To be able to aggregate information expressed as linguistic labels in that ordered linguistic scale the classical operators Max, Min and Neg are used, where:

$Max(s_i,s_j) = S_i if s_i >= s_j,$

$Min(s_i,s_j) = S_i if s_i <= s_j and$

$Neg(s_i) = s_{g-i+1} where g is the cardinality of S.$

Yager (R.R. Yager. Non-numeric multi-criteria multi-person decision making. Group Decision and Negotiation, 2(1):81-93, 1993 doi:10.1007/BF01384404, R.R. Yager. Aggregation of ordinal information. Fuzzy Optimization and Decision Making, 6(3):199-219, 2007 doi:10.1007/s10700-007-9008-8) studies several operators for ordinal information to be able to properly aggregate different linguistic evaluations and studies several operators for ordinal information aggregation as weighted normed operators, uninorm operators, ordinal mean type operators, etc. Buckley (J.J. Buckley. The multiple judge, multiple criteria ranking problem: A fuzzy set approach. Fuzzy Sets and Systems, 13(1):25-37, 1984 doi:10.1016/0165-0114(84)90024-1) uses different variations of the median, max and min operators to aggregate linguistic opinions and criteria.

Linguistic symbolic computational model based on convex combination (M. Delgado, J.L. Verdegay, and M.A. Vila. On aggregation operations of linguistic labels. International Journal of Intelligent Systems, 8(3):351-370, 1993 doi:10.1002/int.4550080303). In this model, the aggregation is made using a convex combination of linguistic labels which directly acts over the label indexes of the linguistic terms set $S={S_0,...,S_g}$ in a recursive way producing a real value on the granularity interval of the linguistic terms set S. Note that this model usually assumes that the cardinality of the linguistic term set is odd and that linguistic labels are symmetrically placed around a middle term. As the result of the aggregation is not usually an integer, that is, does not correspond to one of the labels in S, it is also necessary to introduce an approximation function app_2(.) to obtain a solution on the S terms set:

$$S^n \xrightarrow{\;\; C \;\; }  \left [ 0,g \right ] \xrightarrow{\;\; app_2(·) \;\; } \left \{ 0, ...,g \right \} \xrightarrow{\;\; \;\; } S$$

For example, suppose that we want to aggregate the linguistic values M, L, VL and H from S={N,VL,L,M,H,VH,P}. Then we have that C{M, L, VL, H} = C{S3, S2, S1, S4} = 2.75. Obviously 2.75 is not the label index of any of the terms in S. If we define $app_2(.)$ as the usual round operation, then we would have that the final result of our aggregation process is $S_{round}(2.75) = S_3 = M$. From the example we can conclude that this model for linguistic aggregation also suffers from loss of information.

Aggregation operators that operate in this linguistic model are the Linguistic Ordered Weighted Averaging (LOWA) operator (F. Herrera, E. Herrera-Viedma, and J.L. Verdegay. Direct approach processes in group decision making using linguistic owa operators. Fuzzy Sets and Systems, 79:175-190, 1996 doi:10.1016/0165-0114(95)00162-X) (based on the OWA operator and the convex combination of linguistic labels), the Linguistic Weighted Disjunction (LWD), Linguistic Weighted Conjunction (LWC), the Linguistic Weighted Averaging (LWA) (F. Herrera and E. Herrera-Viedma. Aggregation operators for linguistic weighted information. IEEE Transactions on Systems, Man, and Cyber netics Part A: Systems and Humans, 27(5):646-656, 1997 doi:10.1109/3468.618263), the Linguistic Aggregation of Majority Additive (LAMA) operator ( J.I. Pelelaez and J.M. Doña. Lama: A linguistic aggregation of majority additive operator. International Journal of Intelligent Systems, 18(7):809-820, 2003 doi:10.1002/int.10117) and the Majority Guided Induced Linguistic Aggregation Operators (E. Herrera-Viedma, G. Pasi, A.G. López-Herrera, and C. Porcel. Evaluating the information quality of web sites: A methodology based on fuzzy computing with words. Journal of American Society for Information Science and Technology, 57(4):538–549, 2006 doi:10.1002/asi.20308).

Linguistic symbolic computational model based on virtual linguistic terms (Z.S. Xu. A method based on linguistic aggregation operators for group decision making with linguistic preference relations. Information Sciences, 166(1-4):19–30, 2004 doi:10.1016/j.ins.2003.10.006). In this model, the discrete term set $S = {s_{-g/2},..., s_0,...,s_{-g/2}}$, with g + 1 being the cardinality of S, is extended into a continuous term set $S' = {s_α | α in [-t,t]}$, where t (t > q/2) is a sufficiently large positive integer. If sα in S, then sα is called an original linguistic term, otherwise, sα is called a virtual linguistic term. In the next figure we can see a discrete term set $S = {s_{-3},...,s_3}$ (original linguistic terms) which can be extended to a continuous term set in which virtual linguistic terms as $s_{-0.3}$ in [-3,3] can be obtained and manipulated to avoid loss of information.

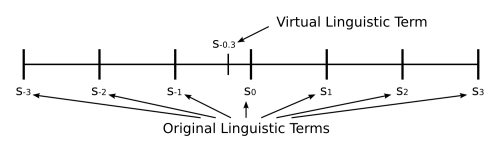
With this extension we can preserve all given information in the problem (thus avoiding one of the biggest problems for the classical linguistic symbolic computational models). Xu states that:

• "In general, the decision maker uses the original linguistic terms to evaluate alternatives, and the virtual linguistic terms only appear in operation".

It is important to note that this symbolic computational model uses a term set that changes during the decision process as new virtual terms are created in the aggregation processes. In addition, this model allows the use of arithmetic operators and the multiplication between a label and a real number which could lead to virtual terms being in a quite different range than the original ones. These facts limit the interpretability of the decision models that implement this computational model. Therefore, this model also presents a retranslation problem if the results of the operations are virtual linguistic terms (and they will usually be virtual ones) and the final results must be expressed in the original linguistic term set. However, as the linguistic symbolic computational model based on linguistic terms is simple, as it avoids loss of information and as virtual linguistic terms can be used to rank alternatives and thus, to select the best of them, its use can be convenient in particular situations.

Several different operators have been defined in order to aggregate linguistic information using this model. For example, some extensions to the classical families of ordered weighted averaging and geometric operators have been presented in (Z.S. Xu. Eowa and eowg operators for aggregating linguistic labels based on linguistic preference relations. International Journal of Uncertainty, Fuzziness and Knowlege-Based Systems, 12(6):791-810, 2004 doi:10.1142/S0218488504003211, Z.S. Xu. Induced uncertain linguistic owa operators applied to group decision making. Information Fusion, 7(2):231-238, 2006 doi:10.1016/j.inffus.2004.06.005).

2-tuple Linguistic Computational Model: A Symbolic Model Extending the Use of Indexes

The 2-tuple linguistic representation model (F. Herrera and L. Martínez. A 2-tuple fuzzy linguistic representation model for computing with words. IEEE Transactions on Fuzzy Systems, 8(6):746–752, 2000 doi:10.1109/91.890332) is a symbolic model that improves the previous one in several ways:

The linguistic computational model based on linguistic 2-tuples carries out processes of CW easily and without loss of information.

The linguistic domain can be treated as continuous, whilst in the classical models it is treated as discrete.

The results of processes of CW are always expressed in the initial linguistic domain extended to a pair of values that include the label and additional information.

To represent the linguistic information, this model uses a pair of values called linguistic 2-tuple (s, α), where s is a linguistic term and α is a numeric value representing a Symbolic Translation:

Definition: Let β be the result of an aggregation of the indexes of a set of labels assessed in a linguistic term set S, i.e., the result of a symbolic aggregation operation. β in [0,g], being g + 1 the cardinality of S. Let i = round(β) and α = β - i be two values, such that, i in [-0.5,0.5) then α is called a Symbolic Translation.

In addition, the model defines a set of transformation functions between numeric values and linguistic 2-tuples:

Definition: Let $S= {s_0,...,s_g}$ be a linguistic term set and β in [0,g] a value representing the result of a symbolic aggregation operation, then the 2-tuple that expresses the equivalent information to β is obtained with the following function:

$$\triangle : \left [ 0,g \right ] \xrightarrow{\;\; \;\; }  S \times [-0.5 , 0.5)$$

$$\triangle (β) = (s_i) , with$$

$$s_i \t i = rount(\beta)$$

$$\in [-0.5 , 0.5)$$

where round(.) is the usual round operation, si has the closest index label to β and α is the value of the symbolic translation. In addition we have:

$$\triangle^{-1} : S \times [-0.5,0.5) \xrightarrow{\;\; \;\; } [0,g]$$

$$\triangle^{-1} (s_i, \alpha ) = i + \alpha = \beta$$

It is obvious that the conversion between a linguistic term into a linguistic 2-tuple consist of adding a value 0 as symbolic translation: $s_i$ in $S --> (s_i,0)$.

In the next figure we can see an example of a 2-tuple linguistic label that express the equivalent information of the result of a symbolic aggregation operation: Suppose that β = 2.7 is a value representing the result of a symbolic aggregation operation on the set of labels $S = { s_0,..., s_6 }$, then the 2-tuple that express the equivalent information to β is $(s_3, -0.3)$.

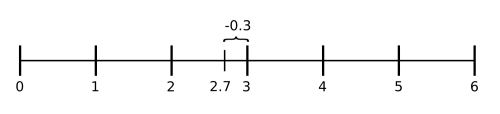
Even being a quite recent model, the 2-tuple model has received a quite good acceptation in the specialized literature and some extensions to the 2-tuple linguistic model have been developed in which the underlying definitions of linguistic labels and linguistic variables are taken into account in the process of aggregating linguistic information by assigning canonical characteristic values of the corresponding linguistic labels (J.-H. Wang and J. Hao. A new version of 2-tuple fuzzy linguistic representation model for computing with words. IEEE Transactions on Fuzzy Systems, 14(3):435-445, 2006 doi:10.1109/TFUZZ.2006.876337, J.-H. Wang and J. Hao. An approach to computing with words based on canonical characteristic values of linguistic labels. IEEE Transactions on Fuzzy Systems, 15(4):593-604, 2007 doi:10.1109/TFUZZ.2006.889844).

The aggregation of 2-tuple linguistic information can be achieved by applying some extensions of classical aggregation operators to the 2-tuple linguistic model that can be found in the literature as the Arithmetic Mean, the Weighted Average Operator, the Ordered Weighted Aggregation (OWA) operator, the LOWA operator, the Lattice-based Linguistic-Valued Weighted Aggregation (LVWA) (X. Li, D. Ruan, J. Liu, and Y. Xu. A linguistic-valued weighted aggregation operator to multiple attribute group decision making with quantative and qualitative information. International Journal of Computational Intelligence Systems, 1(3):274-284, 2008) and the LAMA operator (J.I. Peláez and J.M. Doña. LAMA: A linguistic aggregation of majority additive operator. International Journal of Intelligent Systems, 18(7):809-820, 2003 doi:10.1002/int.10117).

An Historical Perspective: Pioneer Papers in Linguistic Decision Making

R.M. Tong and P.P. Bonissone. A linguistic approach to decisionmaking with fuzzy sets. IEEE Transactions on Systems, Man and Cybernetics SMC-10(11):716--723, 1980 doi:10.1109/TSMC.1980.4308391

The authors stated how a linguistic assessment of a decision can make explicit the subjective nature of any choice that is made using fuzzy information and how developing linguistic approaches can ease decision makers to interact with the decision process at every level. Thus, they propose a technique in which the preference of one alternative over the others can be expressed as a truth qualified proposition in a natural language in the form "It is more or less true that ak is preferred to all others" (where ak is one of the alternatives in the set of feasible alternatives A = {a1,..., an}). They used the linguistic computational model presented in the previous section in which the computations are carried out directly acting over the membership functions associated to the linguistic labels.

Another seminal paper in which CW is applied to multiobjective decision making was written by Yager, 1981:

R.R. Yager. A New Methodology for Ordinal Multiobjective Decisions Based on Fuzzy Sets. Decision Sciences, 12:589-600, 1981 doi:10.1111/j.1540-5915.1981.tb00111.x

Yager emphasized the importance of using linguistic information, not only to provide the preferences of the decision maker, but also to express the importance of the individual objetives, as it is a much more natural approach for a decision maker than just using numbers:

The values to be used for the evaluation of the ratings and importances will be drawn from a linguistic scale which makes it easier for the evaluator to provide the information.

In fact, Yager uses the linguistic symbolic model based on ordinal scales and max-min operators presented in the previous section to solve multiobjective decision problems where not only the information about each alternative is given using linguistic terms but also where the importance of each objective is evaluated linguistically. It was later revisited and extended in 1993 (R.R. Yager. Non-numeric multi-criteria multi-person decision making. Group Decision and Negotiation, 2(1):81–93, 1993 doi:10.1007/BF01384404).

Buckey (1984) also studied decision making problems in a linguistic context in which the best alternative from a feasible set has to be selected by an analyst according the the opinions of several judges which supply information about the alternatives for a set of different criteria:

J.J. Buckley. The multiple judge, multiple criteria ranking problem: A fuzzy set approach. Fuzzy Sets and Systems, 13(1):25-37, 1984 doi:10.1016/0165-0114(84)90024-1

The information supplied by the judges is given using an ordinal scale previously designed by the analyst. Buckley states several reasons for using the ordinal scale instead of other exact, ratio or interval scales, e.g. in problems with a large number of alternatives or criteria it might be easier to provide an element in the ordinal scale than concrete numbers or ratios of numbers, or, in addition, some of the criteria may be vaguely understood or imprecisely defined for the judges. To resolve these problems the author discusses the three main issues that have to be faced to obtain the final ranking of the alternatives:

when to pool, or average, the judges;

how to pool, or average, the judges; and

how to compute the final weight for each alternative.

In this work the linguistic symbolic computational model based on ordinal scales and max-min operators presented in the previous section is used with some variations of the median, max and min operators to aggregate the linguistic information.

Finally, two short contributions published in 1985 dealt with multicriteria optimization problems and selection of models.

M.S. Shendrik and B.G. Tamm. Approach to Interactive Solution of Multicriterial Optimization Problems with Linguistic Modeling of Preferences. Automatic Control and Computer Sciences, 19(6):3-9, 1985

The authors extend a multicriteria optimization algorithm to accept fuzzy linguistic variables and thus, they convert it into a fuzzy linguistic algorithm. In particular they use different linguistic term sets to evaluate the degree to which a decision maker is satisfied with a particular solution and to control the rate of change between different criteria.

V.B. Silov and D.V. Vilenchik. Linguistic Decision-Making Methods in Multicriterial Selection of Models. Soviet Journal of Automation and Information Sciences (English translation of Avtomatyka), 18(4):92-94, 1985

The authors make use of a linguistic model to characterize the preferences of the decision maker in form of rules that take linguistic variables as parameters. Both works use a linguistic computational model based on membership functions.

Recent Applications of CW in Decision Making

In this section we present some of the recent applications (published in the specialized literature in 2007 and 2008) based on a CW approach:

Resource management and transfer

Application	Papers
Sustainable energy management	H.Ch. Doukas, B.M. Andreas, J.E. Psarras. Multi-criteria decision aid for the formulation of sustainable technological energy priorities using linguistic variables. European Journal of Operational Research 182 (2) (2007) 844-855 doi:10.1016/j.ejor.2006.08.037
Water resources management	G. Fu. A fuzzy optimization method for multicriteria decision making: An application to reservoir flood control operation. Expert Systems with Applications 34 (1) (2008) 145-149 doi:10.1016/j.eswa.2006.08.021
Human resources management	T. Yang, M.C. Chen, C.C. Hung. Multiple attribute decision-making methods for the dynamic operator allocation problem. Mathematics and Computers in Simulation 73 (5) (2007) 285-299 doi:10.1016/j.matcom.2006.04.002 Y.H. Sun, J. Ma, Z.P. Fan, J. Wang. A group decision support approach to evaluate experts for R&D project selection. IEEE Transactions on Engineering Management 55 (1) (2008) 158-170 doi:10.1109/TEM.2007.912934 W.S. Tai, C.T. Chen. A new evaluation model for intellectual capital based on computing with linguistic variable. Expert Systems With Applications 36 (2) (2008) 3483-3488 doi:10.1016/j.eswa.2008.02.017
Knowledge management	J.-H. Wang, J. Hao. Fuzzy linguistic PERT. IEEE Transactions on Fuzzy Systems 15 (2) (2007) 133-144 doi:10.1109/TFUZZ.2006.879975
Team situation awareness	J. Lu, G. Zhang, D. Ruan. Intelligent multi-criteria fuzzy group decision-making for situation assessments. Soft Computing 12 (3) (2008) 289-299 doi:10.1007/s00500-007-0197-4

Industry applications

Application	Papers
Supplier selection & evaluation	S.L. Chang, R.C. Wang, S.Y. Wang. Applying a direct multi-granularity linguistic and strategy-oriented aggregation approach on the assessment of supply performance. European Journal of Operational Research 177 (2) (2007) 1013-1025 doi:10.1016/j.ejor.2006.01.032 G.D. Li, D. Yamaguchi, M. Nagai. A grey-based decision-making approach to the supplier selection problem. Mathematical and Computer Modelling 46 (3-4) (2007) 573-581 doi:10.1016/j.mcm.2006.11.021
Location selection	T.Y. Chou, C.L. Hsu, M.C. Chen. A fuzzy multi-criteria decision model for international tourist hotels location selection. International Journal of Hospitality Management 27 (2) (2008) 293-301 doi:10.1016/j.ijhm.2007.07.029 S. Onut, S. Soner. Transshipment site selection using the AHP and TOPSIS approaches under fuzzy environment. Waste Management 28 (9) (2008) 1552-1559 doi:10.1016/j.wasman.2007.05.019 K. Anagnostopoulos, H. Doukas, J. Psarras. A linguistic multicriteria analysis system combining fuzzy sets theory, ideal and anti-ideal points for location site selection. Expert Systems with Applications 35 (4) (2008) 2041-2048 doi:10.1016/j.eswa.2007.08.074
Material, stock and systems selection	H.Y. Lin, P.Y. Hsu, G.J. Sheen. A fuzzy-based decision-making procedure for data warehouse system selection. Expert Systems with Applications 32 (3) (2007) 939-953 doi:10.1016/j.eswa.2006.01.031
Manufacturing flexibility evaluation	S.J. Chuu. Evaluating the flexibility in a manufacturing system using fuzzy multi-attribute group decision-making with multi-granularity linguistic information. International Journal of Advanced Manufacturing Technology 32 (3-4) (2007) doi:10.1007/s00170-005-0342-0

Evaluation and recommendation

Application	Paper
Projects evaluation & selection	G. Buyukozkan, D. Ruan. Evaluation of software development projects using a fuzzy multi-criteria decision approach. Mathematics and Computers in Simulation 77 (5-6) (2008) 464-475 doi:10.1016/j.matcom.2007.11.015
Engineering evaluation	L. Martinez, J. Liu, D. Ruan, J.B. Yang. Dealing with heterogeneous information in engineering evaluation processes. Information Sciences 177 (7) (2007) 1533-1542 doi:10.1016/j.ins.2006.07.005
Sensory evaluation	L. Zou, X. Liu, Z. Wu, and Y. Xu. A uniform approach of linguistic truth values in sensor evaluation. Fuzzy Optimization and Decision Making, 7(4):387–397, 2008 doi:10.1007/s10700-008-9046-x L. Martínez. Sensory evaluation based on linguistic decision analysis. International Journal of Approximate Reasoning 44 (2) (2007) 148-164 doi:10.1016/j.ijar.2006.07.006 L. Martínez, M. Espinilla, and L.G. Perez. A linguistic multigranular sensory evaluation model for olive oil. International Journal of Computational Intelligence Systems, 1(2):148–158, 2008 doi:10.2991/ijcis.2008.1.2.5
Information retrieval	E. Herrera-Viedma and A.G. Lopez-Herrera. A model of information retrieval system with unbalanced fuzzy linguistic information. International Journal Of Intelligent Systems, 22(11):1197–1214, 2007 doi:10.1002/int.20244
Recommender systems	L. Martínez, L.G. Pérez, and M. Barranco. A multi-granular linguistic based-content recommendation model. International Journal of Intelligent Systems, 22(5):419–434, 2007 doi:10.1002/int.20207 L. Martínez, M.J. Barranco, L.G. Perez, and M. Espinilla. A knowledge based recommender system with multigranular linguistic information. International Journal of Computational Intelligence Systems, 1(3):225–236, 2008 doi:10.2991/ijcis.2008.1.3.4
Web quality	E. Herrera-Viedma, E. Peis, J.M. Morales del Castillo, S. Alonso, and E.K. Anaya. A fuzzy linguistic model to evaluate the quality of web sites that store xml documents. International Journal of Approximate Reasoning, 46(1):226–253, 2007 doi:10.1016/j.ijar.2006.12.010 E. Herrera-Viedma, G. Pasi, A.G. López-Herrera, C. Porcel. Evaluating the Information Quality of Web Sites: A Methodology Based on Fuzzy Computing with Words. Journal of the American Society for Information Science and Technology 57 (4) (2006) 538-549 doi:10.1002/asi.20308

Investments applications and risk assessment

Application	Paper
Investments evaluation	G. Shevchenko, L. Ustinovichius, A. Andruskevicius. Multi-attribute analysis of investments risk alternatives in construction. Technological and Economic Development of Economy 14 (3) (2008) 428-443 doi:10.3846/1392-8619.2008.14.428-443
Situation Assessment	J. Lu, G. Zhang, D. Ruan. Intelligent multi-criteria fuzzy group decision-making for situation assessments. Soft Computing 12 (3) (2007) 289-299, doi:10.1007/s00500-007-0197-4
Investment improvement	Z. Gungor, F. ArIkan. Using fuzzy decision making system to improve quality-based investment. Journal of Intelligent Manufacturing 18 (2) (2007) 197-207 doi:10.1007/s10845-007-0016-x
Bridge risk assessment	Y.-M. Wang, T.M.S. Elhag. A fuzzy group decision making approach for bridge risk assessment. Computers and Industrial Engineering 53 (1) (2007) 137-148 doi:10.1016/j.cie.2007.04.009

Current Trends and Prospects of CW in Decision Making

In this section we present some current trends of the CW methodology applied in decision making, along with some open questions and prospects about them. We identify nine current trends:

• To deal with different linguistic expression domains to represent preferences in decision making, i.e, using multi-granular linguistic modelling
• To deal with non-symetrical linguistic domains, i.e, unbalanced linguistic modelling
• To deal with the integration of linguistic and numerical representations of preferences
• To deal with the consistency of the linguistic preferences
• To deal with the Missing Linguistic Information and Incomplete Preference Relations in Decision Making
• To develop the linguistic computational model based on type-2 fuzzy sets
• To develop web and mobile based Linguistic Decision Making processes
• To develop new linguistic computational models based on the paradigm of linguistic expressions
• To develop new linguistic consensus approaches.

Multi-granular linguistic modelling

In many real world situations it is not effective to define a unique linguistic term set to be used by all decision makers. Due to different cultural reasons or different points of view and knowledge about the problem it seems natural to allow decision makers to provide their preferences about the problem using different linguistic term sets, with different cardinalities and with different meanings for each label. For example, in a grading system a decision maker could choose to use a linguistic term set $S_1 = { Low, Medium, High }$ and another decision maker could prefer a linguistic term set with higher granularity as $S_2 = {Very Low, Low, Medium, High, Very High }$ (he might be able to better discriminate his preferences about the alternatives). In those cases where the information can be provided using linguistic term sets with different granularity we talk about multi-granular approaches.

In (F. Herrera, E. Herrera-Viedma, and L. Martínez. A fusion approach for managing multi-granularity linguistic term sets in decision making. Fuzzy Sets and Systems, 114(1):43-58, 2000 doi:10.1016/S0165-0114(98)00093-1) an approach to fusion multi-granular information in decision making was presented. That model selects a basic linguistic term set (BLTS) (with maximum granularity) and defines a transformation function that represents each linguistic performance value as a fuzzy set defined in the BLTS. (F. Herrera and L. Martínez. A model based on linguistic 2-tuples for dealing with multigranular hierarchical linguistic context in multi-expert decision making. IEEE Transactions on Systems, Man, And Cybernetics - Part B: Cybernetics, 31(2):227-234, 2001 doi:10.1109/3477.915345) extend this methodology to deal with multi-granular hierarchical linguistic information using the 2-tuple linguistic model. In this model the linguistic term sets must have a hierarchical structure (see the next figure). This model has been used and extended in:

S.-L. Chang, R.-C. Wang, and S.-Y. Wang. Applying a direct multi-granularity linguistic and strategy-oriented aggregation approach on the assessment of supply performance. European Journal of Operational Research, 177(2):1013-1025, 2007 doi:10.1016/j.ejor.2006.01.032

S.-J. Chuu. Evaluating the flexibility in a manufacturing system using fuzzy multi-attribute group decision-making with multi-granularity linguistic information. International Journal of Advanced Manufacturing Technology, 32(3-4):409-421, 2007 doi:10.1007/s00170-005-0342-0

V. N. Huynh and Y Nakamori. A satisfactory-oriented approach to multi-expert decision-making under linguistic assessments. IEEE Trans. Systems, Man, and Cybernetics, SMC-35(2):184-196, 2005 doi:10.1109/TSMCB.2004.842248

L. Martínez, J. Liu, J.-B. Yang, and F. Herrera. A multigranular hierarchical linguistic model for design evaluation based on safety and cost analysis. International Journal of Intelligent Systems, 20(12):1161-1194, 2005 doi:10.1002/int.20107

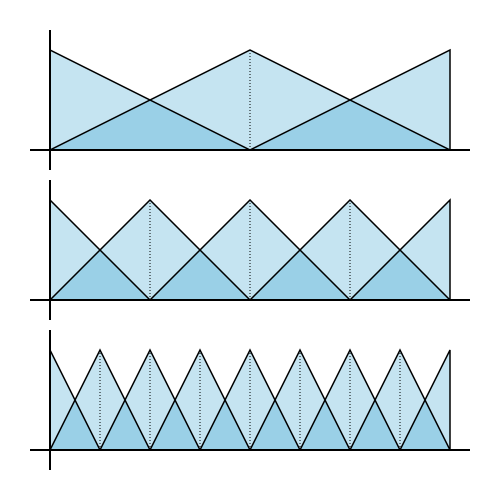
In the most recent literature we can find some new multi-granular approaches such as (Z. Chen and D. Ben-Arieh. On the fusion of multi-granularity linguistic label sets in group decision making. Computers and Industrial Engineering, 51(3):526-541, 2006 doi:10.1016/j.cie.2006.08.012) where the authors propose a new fusion approach of multi-granularity linguistic information for managing information assessed in different linguistic term sets, and (Y.-P. Jiang, Z.-P. Fan, and J. Ma. A method for group decision making with multi-granularity linguistic assessment information. Information Sciences, 178(4):1098–1109, 2008 doi:10.1016/j.ins.2007.09.007) where a new method is presented to solve group decision making problems with multi-granularity linguistic assessments in which the multi-granularity linguistic information provided by decision makers is expressed in the form of fuzzy numbers and a linear goal programming model is constructed to integrate the fuzzy assessment information and to directly compute the collective ranking values of alternatives without the need of information transformation.

There are still some open questions about this topic that must be addressed to build more effective multi-granular Linguistic Decision Making models:

• To make the models more flexible to avoid the restrictions imposed in the term sets (such as the linguistic hierarchy or the even coverage of the universe of discourse by the labels) and thus, to be able to use linguistic terms with an arbitrary granularity.
• Is it possible to minimize the computation efforts required to obtain the final choices using multigranular linguistic information?

Unbalanced linguistic modelling

Unbalanced information situations, that is, situations where the linguistic labels in the terms set are not evenly distributed around a central term, appear in many real world situations. For example, in grading systems, it is common to use unbalanced term sets where only one term represents a negative evaluation and several positive terms represent different grades of success. In the next figure we present an example of an unbalanced term set for grading evaluation S= {F, D, C, B, A} where only one term (F) is used for a negative evaluation and the rest of terms represent different degrees of success.

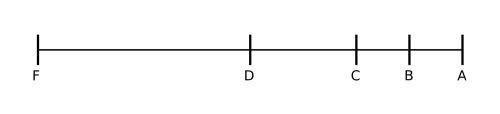
In (F. Herrera, E. Herrera-Viedma, and L. Martínez. A fuzzy linguistic methodology to deal with unbalanced linguistic term sets. IEEE Transactions on Fuzzy Systems, 16(2):354–370, 2008 doi:10.1109/TFUZZ.2007.896353) a model based on linguistic hierarchies was presented to deal with this kind of situations. The Jiang model (Y.-P. Jiang, Z.-P. Fan, and J. Ma. A method for group decision making with multi-granularity linguistic assessment information. Information Sciences, 178(4):1098–1109, 2008 doi:10.1016/j.ins.2007.09.007) proposed for multi-granular environments is also able to deal with unbalanced term sets.

The use of unbalanced linguistic information in decision making is still in an early stage of development and several future challenges are still to be solved:

Development of models that allow the use of any unbalanced term set.

Development of models that integrate both unbalanced and multigranular linguistic approaches.

To analize the potential use of related work regarding antonyms in linguistic environments that has been developed:

• V. Torra. Negation functions based semantics for ordered linguistic labels. International Journal of Intelligent Systems, 11(11):975–988, 1996 doi:10.1002/(SICI)1098-111X(199611)11:11<975::AID-INT5>3.0.CO;2-W
• V. Torra. Aggregation of linguistic labels when semantics is based on antonyms. International Journal of Intelligent Systems, 16:513–524, 2001 doi:10.1002/int.1021
• E. Trillas and S. Guadarrama. What about fuzzy logic's linguistic sound-ness? Fuzzy Sets and Systems, 156(3):334–340, 2005 doi:10.1016/j.fss.2005.05.028

Integration of linguistic and numerical representations of preferences

In real decision making processes, where experts might have a different experience or perception about the alternatives or where the criteria might have a different nature, it is natural to think that the different evaluations about the alternatives can be expressed using different representation formats. In those cases with heterogeneous preference structures we need special mechanisms to allow the integration of evaluations (F. Chiclana, F. Herrera, and E. Herrera-Viedma. Integrating three representation models in fuzzy multipurpose decision making based on fuzzy preference relations. Fuzzy Sets and Systems, 97:33–48, 1998 ).

In fact, it is not unusual to find decision problems in which the information about the alternatives is presented in both a linguistic and a numerical form. Thus, in the literature we can find several approaches that try to incorporate both qualitative and quantitative information to decision making models:

• M. Delgado, F. Herrera, E. Herrera-Viedma, and L. Martínez. Combining numerical and linguistic information in group decision making. Information Sciences, 107(1-4):177–194, 1998 doi:10.1016/S0020-0255(97)10044-5
• P.J. Sánchez F. Herrera, L. Martínez. Managing non-homogeneous information in group decision making. European Journal of Operational Research, 166:115–132, 2005 doi:10.1016/j.ejor.2003.11.031
• P. Meesad and G.G. Yen. Combined numerical and linguistic knowledge representation and its application to medical diagnosis. IEEE Transactions on Systems, Man, and Cybernetics Part A: Systems and Humans, 33(2):206–222, 2003 doi:10.1109/TSMCA.2003.811290

Some important points are still open:

• Is it possible to develop new transformation operators from numerical to linguistic information (an vice versa)?.
• To develop aggregation operators that simultaneously deal with both quantitative and qualitative data.

Consistency of the linguistic preferences

In decision processes it is usually desirable to be able to measure the consistency (lack of contradiction) of the information provided by the decision makers. Non-contradictory information is usually considered more valuable than contradictory one and thus, to develop models to control consistency is usually a good idea in decision making environments. There have been efforts to characterize consistency for many types of preferences (usually by means of different transitivity properties):

• J.L. García-Lapresta and L.C. Meneses. An empirical analysis of transitivity with four scaled preferential judgment modalities. Review of Economic Design, 8(3):335–346, 2003 doi: 10.1007/s10058-003-0105-z
• S. Díaz, S. Montes, and B. De Baets. Transitivity bounds in additive fuzzy preference structures. IEEE Transactions on Fuzzy Systems, 15(2):275-286, 2007 doi: 10.1109/TFUZZ.2006.880004
• E. Herrera-Viedma, F. Herrera, F. Chiclana, and M. Luque. Some issues on consistency of fuzzy preference relations. European Journal of Operational Research, 154(1):98–109, 2004 doi: 10.1016/S0377-2217(02)00725-7
• F. Chiclana, E. Herrera-Viedma, S. Alonso, F. Herrera, Cardinal Consistency of Reciprocal Preference Relations: A Characterization of Multiplicative Transitivity. IEEE Transactions on Fuzzy Systems 17(1): 14-23, 2009 doi: 10.1109/TFUZZ.2008.2008028

Classical approaches to tackle and study of consistency are now being adapted to the linguistic framework. In (Z. Sahnoun, F. DiCesare, and P.P. Bonissone. Efficient methods of computing linguistic consistency. Fuzzy Sets and Systems, 39(1):15–26, 1991 doi:10.1016/0165-0114(91)90062-U) the authors propose a method to obtain a fuzzy measure of the consistency of linguistic information by applying some operators over the membership functions associated to the linguistic terms. In (Y. Dong, Y. Xu, and H. Li. On consistency measures of linguistic preference relations. European Journal of Operational Research, 189(2):430–444,2008 doi:10.1016/j.ejor.2007.06.013) some consistency measures have been developed for linguistic preference relations.

There are still some interesting questions in the field to be solved:

• Design new consitency measures for different kinds of linguistic preference structures.
• Developed consistency measures are usually numerical ones, but it seems natural to think that they might have a qualitative nature. Thus, linguistic consistency measures need to be developed.
• Is it always interesting that decision makers comply with some consistency property?: Although consistent information is usually desired, in some environments some loss of consistency can introduce more diversity on the decision process (which could lead to more discussion and a possible better final solution). Consecuently, it is interesting to study this kind of situations and to develop models that allow to correctly tackle inconsistent information.

Missing Linguistic Information and Incomplete Preference Relations in Decision Making

In real group decision making processes the information about the alternatives is not always complete, that is, the decision makers may not give all the information that they are requested (S.H. Kim and B.S. Ahn. Group decision making procedure considering preference strength under incomplete information. Computers & Operations Research, 24(12):1101–1112, 1997 doi: 10.1016/S0305-0548(97)00037-3). There are several possible reasons for a decision maker not giving complete preferences: he might not have a clear opinion about an alternative, he might not be able to compare some alternatives or he might prefer to avoid giving some preference values to avoid introducing inconsistency in his expressed preferences.

In some recent contributions, the issue of missing linguistic information in decision making environments has been addressed:

• In (D.-F. Li and T. Sun. Fuzzy linmap method for multiattribute group decision making with linguistic variables and incomplete information. International Journal of Uncertainty, Fuzziness and Knowlege-Based Systems,15(2):153–173, 2007 doi:10.1142/S0218488507004509) a linear programming approach for multiattribute linguistic group decision making which is able to deal with incomplete information has been developed,
• in (Z.S. Xu. Incomplete linguistic preference relations and their fusion. Information Fusion, 7(3):331–337, 2006 doi:10.1016/j.inffus.2005.01.003) incomplete linguistic preference relations and their fusion are studied and
• in (S. Alonso, F.J. Cabrerizo, F. Chiclana, F. Herrera, and E. Herrera- Viedma. Group decision making with incomplete fuzzy linguistic preference relations. International Journal of Intelligent Systems, 24(2):201– 222, 2009 doi:10.1002/int.20332) a group decision making approach with incomplete linguistic preference relations, based on consistency properties to estimate missing information, is presented. This later work is an extension from a non-linguistic approach previously presented in (E. Herrera-Viedma, F. Chiclana, F. Herrera, S. Alonso, Group Decision-Making Model with Incomplete Fuzzy Preference Relations Based on Additive Consistency. IEEE Transactions on Systems, Man and Cybernetics, Part B, Cybernetics, 37:1 (2007) 176-189 doi:10.1109/TSMCB.2006.875872) and (E. Herrera-Viedma, S. Alonso, F. Chiclana, F. Herrera, A Consensus Model for Group Decision Making with Incomplete Fuzzy Preference Relations. IEEE Transactions on Fuzzy Systems 15:5 (2007) 863-877 doi:10.1109/TFUZZ.2006.889952)

Some issues still remain open in this field:

• To adapt existing linguistic decision models to deal with incomplete information situations.
• To study in greater detail how different consistency properties can be used to estimate missing information.

Linguistic computational model based on type-2 fuzzy sets

The use of the linguistic semantic model based on type-2 fuzzy sets is a current trend in decision making (J.M. Mendel. An architecture for making judgement using computing with words. International Journal of Applied Mathematics and Computer Sciences, 12(3):325–335, 2002). Several recent works have developed new decision making models in which the linguistic information is computed and aggregated by means of interval type-2 fuzzy sets to maintain a higher (and more realistic) degree of uncertainty of the linguistic information: in (W. Dongrui and J.M. Mendel. Aggregation using the linguistic weighted average and interval type-2 fuzzy sets. IEEE Transactions on Fuzzy Systems, 15(6):1145–1161, 2007 doi:10.1109/TFUZZ.2007.896325) the problem of aggregating linguistic information using a type-2 linguistic model is addressed and in (J. M. Mendel and H. Wu. Type-2 fuzzistics for symmetric interval type-2 fuzzy sets–part 1: Forward problems. IEEE Transactions on Fuzzy Systems, 14(6):781–792, 2006 doi: 10.1109/TFUZZ.2006.881441, J. M. Mendel and H. Wu. Type-2 fuzzistics for symmetric interval type-2 fuzzy sets–part 2: Inverse problems. IEEE Transactions on Fuzzy Systems, 15(2):301–308, 2007 doi: 10.1109/TFUZZ.2006.881447) how to transform linguistic perceptions into interval type-2 fuzzy sets has been considered.

However, several questions are still open:

• What is the limit of uncertainty for CW? Is it interesting to use different kinds of type-2 fuzzy sets? (not only interval ones).
• How to solve the retranslation problem for type-2 fuzzy sets in decision making?
• To develop complete decision models using the linguistic model based on type-2 fuzzy sets.
• To decrease the computational complexity of dealing with type-2 fuzzy sets in decision making.

Web and mobile based Linguistic Decision Making

Decision Support Systems (C.W. Holsapple F. Burstein, editor. Handbook on Decision Support Systems 1. Springer-Verlag, 2008.) have become a major area of interest in the decision making field. Nowadays, time and space constraints, the difficulty of assessing large numbers of alternatives and the necessity of carrying out decision making processes in distributed environments make the use of this kind of systems almost indispensable to solve complex decision making problems. Moreover, as information technologies evolve, there is a greater need to develop new decision support systems to be used in situations where decision makers cannot directly meet together to solve the decision problem. To do so, it is necessary to study current web and mobile technologies and adapt the existing decision models and decision support systems to carry this kind of distributed processes efficiently.

There have been some initial efforts in the field (S. Alonso, S. Arambourg, F.J. Cabrerizo, and E. Herrera-Viedma. Implementation of a mobile group decision making support system with incomplete information. In Proceedings of the 8th International FLINS Conference on Computational Intelligence in Decision and Control, Madrid (Spain), pages 775–780, 2008) but there are many future developments still to be addressed:

• To adapt existing decision support systems to linguistic environments.
• To research on new linguistic interfaces to capture decision makers qualitative preferences.
• To adapt the linguistic decision support systems to distributed environments using web or mobile technologies.

Models based on the paradigm of linguistic expressions

Almost all of the current approaches for CW in decision making use simple labels for alternatives evaluation. However, the use of linguistic expressions could probably provide a much richer environment to solve complex decision making problems. For example, Ma et al. (Y. Xu J. Ma, D. Ruan and G. Zhang. A fuzzy-set approach to treat determinacy and consistency of linguistic terms in multi-criteria decision making. International Journal of Approximate Reasoning, 44(2):165–181, 2007 doi:10.1016/j.ijar.2006.07.007) introduce the possibility of using a set of labels for evaluating an alternative by experts. They analyze the determinacy of linguistic term sets and their consistency (in real applications, those linguistic terms used by experts in individual evaluations should be consistent enough). Tang et al. (Y. Tang and J. Zheng. Linguistic modelling based on semantic similarity relation among linguistic labels. Fuzzy Sets and Systems, 157(12):1662– 1673, 2006 doi:10.1016/j.fss.2006.02.014) present a proposal that allows to compute the semantic similiarty between a linguistic expression and basic linguistic labels, using the mass assignmnet to labels. Focused on linguistic decision problems, it allows to describe an object (alternative) using a linguistic expression (such as NOT label).

To do so, several questions still have to be answered:

• When should linguistic expressions be used in decision making?
• How can linguistic expressions be aggregated?
• How can linguistic expressions be used in multi-granular environments?

Linguistic consensus approaches

Consensus reaching is a transverse topic in the decision making field. To obtain a high degree of consensus or agreement among the decision makers is usually a crucial aspect of any group decision making problem (S. Saint and J. R. Lawson. Rules for Reaching Consensus. A Modern Approach to Decision Making. San Francisco, CA: Jossey-Bass, 1994). Many decision making approaches include an initial iterative consensus phase (prior to the selection of the best alternative) in order to reach a desired level of agreement. In the next figure we can see a general scheme of a group decision making process in which a set of solution alternatives is presented to the decision makers (experts) which express their preferences about it. If the moderator detects that there is not enough consensus he will urge them to change their preferences (he might even give them recommendations about how to change them) and another consensus round starts. If the consensus level is high enough, the selection process is applied and the final solution is selected.

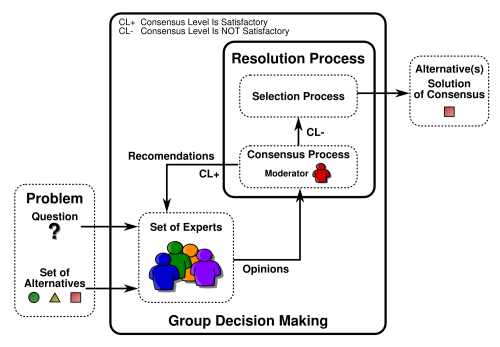
In the literature we can find several consensus models with linguistic information:

• Two classical papers by Herrera et al. (F. Herrera, E. Herrera-Viedma, and J.L. Verdegay. A model of consensus in group decision making under linguistic assessments. Fuzzy Sets and Systems, 78:73–87, 1996 doi:10.1016/0165-0114(95)00107-7) and Bordogna et al. (G. Bordogna, M. Fedrizzi, and G. Pasi. A linguistic modeling of consensus in group decision making based on owa operators. IEEE Transactions on Systems, Man, and Cybernetics Part A: Systems and Humans, 27(1):126–132, 1997 doi:10.1109/3468.553232) developed consensus models for decision making with linguistic assessments.

In addition, many of the current trends presented in previous sections have been applied in conjunction with the consensus reaching topic. For example:

• Herrera-Viedma et al. (E. Herrera-Viedma, L. Martínez, F. Mata, and F. Chiclana. A consensus support system model for group decision-making problems with multigranular linguistic preference relations. IEEE Transactions on Fuzzy Systems,13(5):644–658, 2005 doi:10.1109/TFUZZ.2005.856561) developed a consensus support system with multigranular linguistic information,
• Ben-Arieh et al. (D. Ben-Arieh and Z. Chen. Linguistic-labels aggregation and consensus measures for autocratic decision making using group recommendations. IEEE Transactions on Systems, Man, and Cybernetics Part A: Systems and Humans, 36(3):558–568, 2006 doi:10.1109/TSMCA.2005.853488) developed some consensus measures to guide a Linguistic Decision Making process,
• Cabrerizo et al.(F.J. Cabrerizo, S. Alonso, and E. Herrera-Viedma. A consensus model for group decision making problems with unbalanced fuzzy linguistic information. International Journal of Information Technology & Decision Making, 8(1):1–23, 2009 doi:10.1142/S0219622009003296) presented a consensus model with linguistic unbalanced information,
• García-Lapresta (J.L. García-Lapresta. A general class of simple majority decision rules based on linguistic opinions. Information Sciences, 176:352–365, 2006 doi:10.1016/j.ins.2005.07.004) studied the related concept of majority in decision linguistic environments and
• Cassone et al. (D. Cassone and D. Ben-Arieh. Successive proportional additive numeration using fuzzy linguistic labels (fuzzy linguistic span). Fuzzy Optimization and Decision Making, 4(3):155–174, 2005 doi:10.1007/s10700-005-1886-z) adapted the classical Successive Proportional Additive Numeration (SPAN) consensus technique to use fuzzy linguistic labels.

There are still some open questions about this topic to be addressed:

• To develop new consensus models which incorporate feedback mechanisms to help decison makers to achieve a high level of consensus based on rules easy to understand and to apply by the experts.
• To create or adapt consensus models to consider new linguistic representation formats or expressions.
• To make use of new web and mobile technologies to implement consensus models and consensus support systems in distributed decision making environments.

Special Issues Devoted to Computing with Words and Decision Making

There have been several Special Issues devoted to Computing with Words and Decision Making:

	F. Herrera, S. Alonso, F. Chiclana, E. Herrera-Viedma (Eds.), Computing with Words and Decision Making, Special Issue of Fuzzy Optimization and Decision Making, Volume 8, Number 4 (December 2009). Table Of Contents
	L. Martínez, D. Ruan, F. Herrera, E. Herrera-Viedma, P.P. Wang (Eds.), Special Issue on Linguistic decision making: Tools and applications, Information Sciences, Volume 179, Issue 14 (June 2009). Table Of Contents
	F. Herrera, E. Herrera-Viedma, L. Martínez, P.P. Wang (Eds.), Special Issue on recent advancements of fuzzy sets: Theory and practice. Information Sciences. Volume 176, Issue 4, 2006. Table Of Contents
	D. Rutkowska, J. Kacprzyk, L.A. Zadeh (Eds.), Computing with Words and Perceptions, Special Issue of International Journal of Applied Mathematics and Computer Science, Volume 12, Issue 3, 2002. Table Of Contents
	F. Herrera and E. Herrera-Viedma (Eds.), Computing with Words: Foundations and Applications. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems (IJUFKS), Volume 9, Suppl: 1-2 September 2001. Table Of Contents

In addition, the reader can increase the information provided in this web page. To do so, we recommend the following books:

	P.P. Wang, editor. Computing with Words. Wiley Series on Intelligent Systems. John Wiley & Sons, Inc., 2001. ISBN: 978-0471353744
	L. Zadeh and J. Kacprzyk, editors. Computing with Words in Information / Intelligent Systems 1 (Foundations), volume 33 of Studies in Fuzziness and Soft Computing. Springer-Verlag, 1999. ISBN: 978-3790812176
	L. Zadeh and J. Kacprzyk, editors. Computing with Words in Information / Intelligent Systems 2 (Applications), volume 34 of Studies in Fuzziness and Soft Computing. Springer-Verlag, 1999. ISBN: 978-3790812183

Bibliography Compilation about CW in Decision Making

We have performed a bibliography compilation of journal papers on h-index and related areas. It is maintained by S. Alonso.

If you would like to include or correct any of the references on this page, please contact the maintainer in his e-mail address: zerjioi@ugr.es