This Website contains SCI²S research material on Semi-Supervised Classification. This research is related to the following SCI²S papers published recently:

• I. Triguero, S. García, F. Herrera, Self-Labeled Techniques for Semi-Supervised Learning: Taxonomy, Software and Empirical Study. Knowledge and Information Systems, COMPLEMENTARY MATERIAL to the paper here: datasets, experimental results and source codes. doi: 10.1007/s10115-013-0706-y, in press (2014).
• I. Triguero, José A. Sáez, J. Luengo, S. García, F. Herrera, On the Characterization of Noise Filters for Self-Training Semi-Supervised in Nearest Neighbor Classification. Neurocomputing 132 (2014) 30-41, doi: 10.1016/j.neucom.2013.05.055
• I. Triguero, S. García, F. Herrera , SEG-SSC: A Framework based on Synthetic Examples Generation for Self-Labeled Semi-Supervised Classification. IEEE Transactions on Cybernetics 45:4 (2015) 622-634, doi: 10.1109/TCYB.2014.2332003.

The web is organized according to the following Summary:

1. Introduction to Semi-Supervised Classification
2. Self-Labeled Classification
   1. Background
   2. Taxonomy
   3. Self-Labeled Methods
   4. Experimental Analyses
3. Other Approaches to tackle Semi-Supervised Classification
   1. Generative models
   2. Graph-based
   3. Semi-supervised support vector machines
4. Other problems connected with Semi-supervised Classification
   1. Semi-supervised Clustering
   2. Active Learning
   3. Semi-Supervised Dimensionality Reduction
   4. Self-Supervised
   5. Partial Label
5. The impact of Semi-Supervised Classification
6. Software, Algorithm Implementations and Dataset Repository

Introduction to Semi-Supervised Classification

The Semi-Supervised Learning (SSL) paradigm (Zhu X, Goldberg AB (2009) Introduction to semi-supervised learning, 1st edn. Morgan and Claypool, San Rafael, CA.) has attracted much attention in many different fields ranging from bioinformatics to Web mining, where it is easier to obtain unlabeled than labeled data because it requires less effort, expertise and time consumption. In this context, traditional supervised learning is limited to using labeled data to build a model. Nevertheless, SSL is a learning paradigm concerned with the design of models in the presence of both labeled and unlabeled data. SSL is an extension of unsupervised and supervised learning by including additional information typical of the other learning paradigm. Depending on the main objective of the methods, we can divide SSL into:

1. Semi-Supervised Classification (SSC): It focuses on enhancing supervised classification by minimizing errors in the labeled examples, but it must also be compatible with the input distribution of unlabeled instances.
2. Semi-Supervised Clustering: Also known as constrained clustering, it aims to obtain better-defined clusters than those obtained from unlabeled data. (Pedrycz W (1985) Algorithms of fuzzy clustering with partial supervision. Pattern Recognit Lett 3:13-20.)

SSC can be categorized into two slightly different settings [7], denoted transductive and inductive learning.

1. Transductive learning: It concerns the problem of predicting the labels of the unlabeled examples, given in advance, by taking both labeled and unlabeled data together into account to train a classifier.
2. Inductive learning: It considers the given labeled and unlabeled data as the training examples, and its objective is to predict unseen data.

Existing SSC algorithms are usually classified depending on the conjectures they make about the relation of labeled and unlabeled data distributions. Broadly speaking, they are based on the manifold and/or cluster assumption. The manifold assumption is satisfied if data lie approximately on a manifold of lower dimensionality than the input space. The cluster assumption states that similar examples should have the same label. Graph-based models are the most common approaches to implementing the manifold assumption. As regards examples of models based on the cluster assumption, we can find generative models or semi-supervised support vector machines. Recent studies have addressed multiple assumptions in one model (K. Chen and S. Wang, Semi-supervised learning via regularized boosting working on multiple semi-supervised assumptions, IEEE Trans. Pattern Anal. Mach. Intell., vol. 33, no. 1, pp. 129-143, Jan. 2011).
In addition to these techniques, Self-labeled techniques are SSC methods that do not make any specific suppositions about the input data. These models use unlabeled data within a supervised framework via a self-training process. These techniques aim to obtain one (or several) enlarged labeled set(s), based on their most confident predictions, to classify unlabeled data.

In this website, we will provide an outlook of the Semi-Supervised Classification field, focusing on Self-labeling techniques (Section 2). Background information, taxonomy and method's references are given, as well as a full set of experimental results obtained through the application of the techniques over a set of well-known supervised classification problems. SCI2S contributions in this field are also outlined. Furthermore, we also take into consideration other approaches to face SSC, describing the most important milestones in its development (Section 3). Next, we will also mention other problems that are closely realted to SSC (Section 4), explaining their similarities and offering recent works. Moreover, we will investagate the influence of SSC in the specialized literature by performing a Visibility analysis of this area a the Web of Science (WoS) (Section 5). Finally, we present the software we have developed within the KEEL framework to tackle SSC, including source codes as well as a dataset repository (Section 6).

Self-Labeled Classification

Background

The SSC problem can be defined as follows: Let x_p be an example where x_p = (x_p1 , x_p2, ..., x _pD, ω), with x_pbelonging to a class ω and a D-dimensional space in which x_pi is the value of the ith feature of the pth sample. Then, let us assume that there is a labeled set L which consists of n instances x_p with ω known. Furthermore, there is an unlabeled set U which consists of m instances x_q with ω unknown, let m > n. The L &up; U set forms the training set (denoted as TR). The purpose of SSC is to obtain a robust learned hypothesis using TR instead of L alone, which can be applied in two slightly different settings: transductive and inductive learning.

Transductive learning is described as the application of an SSC technique to classify all the m instances x_p of U correctly. The class assignment should represent the distribution of the classes efficiently, based on the input distribution of unlabeled instances and the L instances.

Let TS be a test set composed of t unseen instances x_rwith ω unknown, which has not been used at the training stage of the SSC technique. The inductive learning phase consists of correctly classifying the instances of TS based on the previously learned hypothesis.

Taxonomy

Self-labeled methods search iteratively for one or several enlarged labeled set(s) (EL) of prototypes to efficiently represent the TR. The Self-labeling taxonomy is oriented to categorize the algorithms regarding four main aspects related to their operation:

• Addition mechanism: There are a variety of schemes in which an EL is formed.
  • Incremental: A strictly incremental approach begins with an enlarged labeled set EL=L, and adds, step-by-step, the most confident instances of U if they fulfill certain criteria. In this case, the algorithm crucially depends on the way in which it determines the confidence predictions of each unlabeled instance; that is, the probability of belonging to each class. Under such a scheme, the order in which the instances are added to the EL determines the learning hypotheses and therefore the following stages of the algorithm. One of the most important aspects of this approach is the number of instances added in each iteration. On the one hand, this number could be defined as a constant parameter and/or independent of the classes of the instances. On the other hand, it can be chosen as a proportional value of the number of instances of each class in L.
  • Batch: Another way to generate an EL set is in batch mode. This involves deciding if each instance meets the addition criteria before adding any of them to the EL. Then all those that do meet the criteria are added at once. In this sense, batch techniques do not assign a definitive class to each unlabeled instance during the learning process. They can reprioritize the hypotheses obtained from labeled samples. Batch processing suffers from increased time complexity over incremental algorithms.
  • Amending: Amending models appeared as a solution to the main drawback of the strictly incremental approach. In this approach, the algorithm starts with EL=L, and iteratively can add or remove any instance which meets the specific criterion. This mechanism allows rectifications to already performed operations and its main advantage is to make the achievement of a good accuracy-suited EL set of instances easy. As in the incremental approach its behavior can also depend on the number of instances added per iteration.
• Single-classifier versus multi-classifier: Self-labeled techniques can use one or more classifiers during the enlarging phase of the labeled set. As we stated before, all of these methods follow a wrapper methodology using classifier(s) to establish the possible class of unlabeled instances.
  • Single-classifier models: Each unlabeled instance belongs to the most probable class assigned by the uniquely used classifier. It implies that these probabilities should be explicitly measured. There are different ways in which these confidences are computed. For example, in probabilistic models, such as Naive Bayes, the confidence predictions can usually be measured as the output probability in prediction, and other methods, such as Nearest Neighbor could approximate confidence in terms of distance. In general, the main advantage of single-classifier methods is their simplicity, allowing us to compute faster confidence probabilities.
  • Multi-classifier models: They combine the learned hypotheses with several classifiers to predict the class of unlabeled instances. The underlying idea of using multi-classifiers in SSL is that several weak classifiers, learned with a small number of instances, can produce better generalization capabilities than only one weak classifier. These methods are motivated, in part, by the empirical success of ensemble methods. Two different approaches are commonly used to calculate the confidence predictions in multi-classifier methods: agreement of classifiers and combination of the probabilities obtained by single-classifiers. These techniques usually obtain a more accurate precision than single-classifier models. Another effect of using several classifiers in self-labeled techniques is their complexity.
• Single-learning versus multi-learning: Apart from the number of classifiers, a key concern is whether they are constituted by the same (single) or different (multiple) learning algorithms. The number of different learning algorithms used can also determine the confidence predictions of unlabeled data.
  • Single-learning: It could be linked to both single and multi-classifiers. With a single-learning algorithm, the confidence prediction measurement is relaxed with regard to the rest of the properties, type of view and number of classifiers. The goal of this approach, which has been shown to perform well in several domains, is simplicity.
  • Multi-learning: With this approach, the confidence predictions are computed as the integration of a group of different kinds of learners to boost the performance classification. It works under the hypothesis that different learning techniques present different behaviors, using the bias classification between them, which generate locally different models. Multi-learning methods are closely linked with multi-classifier models. A multi-learning method is itself a multi-classifier method in which the different classifiers come from different learning methods. Hence, the general properties explained above for multi-classifiers are also extrapolated to multi-learning. A specific drawback of this approach is the choice of the most adequate learning approaches.
• Single-view versus multi-view: This characteristic refers to the way in which the input feature space is taken into consideration by the self-labeled technique.
  • Single-view: A single-view self-labeled technique does not make any specific assumptions for the input data. Hence, it uses the complete L to train. Most of the self-labeled techniques adhere to this due to the fact that in many real-world data sets the feature input space cannot be appropriately divided into conditionally independent views
  • Multi-view: In a multi-view self-labeled technique, L is split into two or more subsets of the features L_k of dimension M (M

Figure 1 shows a map of the taxonomy, categorizing all the Self-labeled methods described in this website. Later, they will be described and referenced.

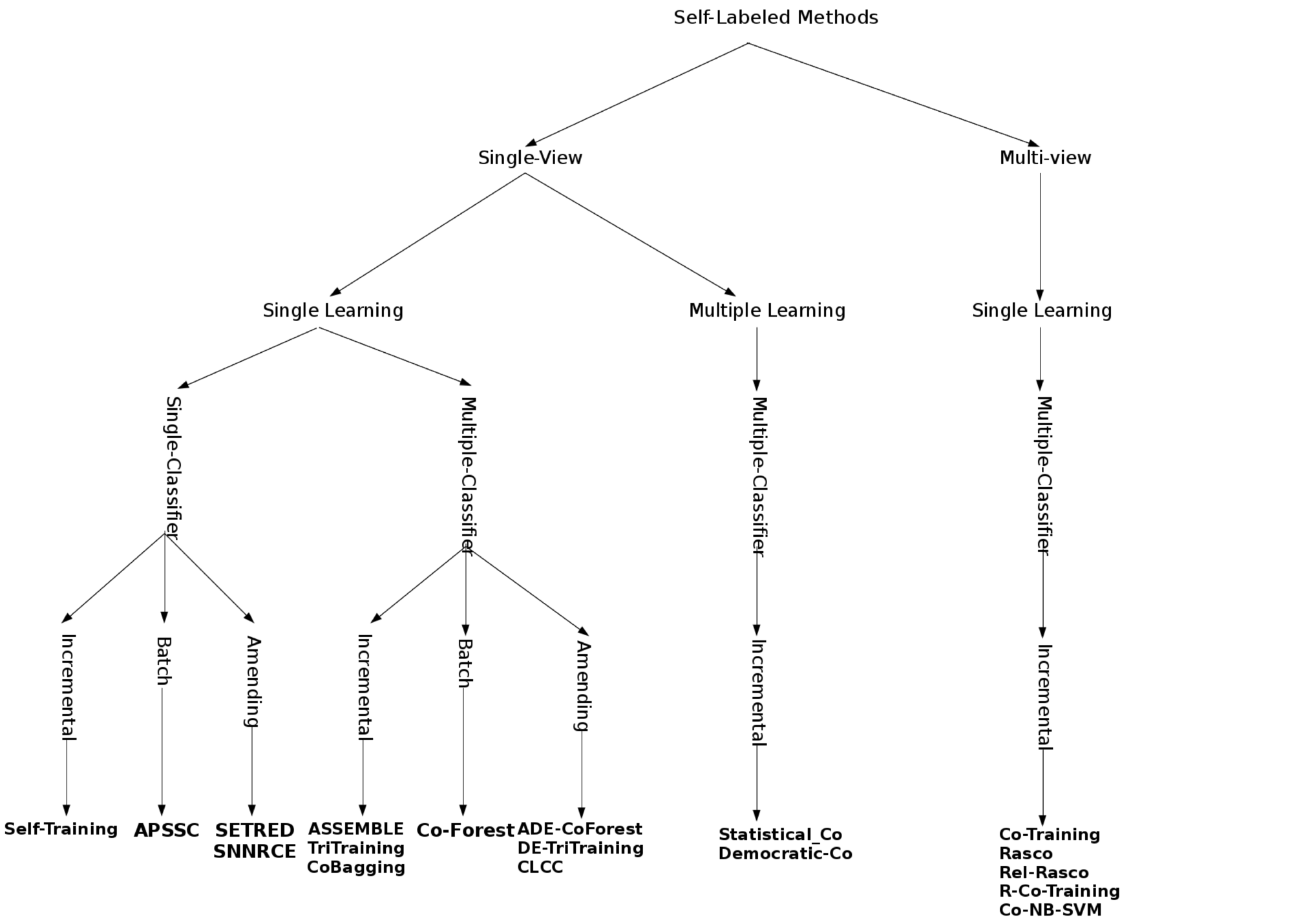
Figure 1. Self-labeled techniques hierarchy

Apart from the previous characteristics, we may remakr upon other properties that explore how self-labeled methods work.

• Confidence measures: An inaccurate confidence measure leads to adding mislabeled examples to the EL which implies a performance degradation of the self-labeling process. The previously explained characteristics define in a global manner the way in which the confidence predictions are estimated. Nevertheless, the specific combination of these characteristics lead to different ideas to establish these probabilities.
• Self-teaching versus mutual-teaching: This property refers to the posibility that classifiers may teach each other their most confident predicted examples.
• Stopping criteria: This is related to the mechanism used to stop the self-labeling process. It is an important factor due to the fact that it implies the size of the EL formed and therefore in the learned hypothesis. Three main approaches can be found in the literature. Firstly, in classical approaches such as self-training, the self-labeling process is repeated until all the instances from U have been added to EL. If erroneous unlabeled instances are added to the EL, they can damage the classification performance.

Self-Labeled Methods

In this section we provides the references of current Self-labeling approaches:

• 1995
  • Standard self-training (Self-Training)

    Yarowsky D (1995) Unsupervised word sense disambiguation rivaling supervised methods. In: Proceedings of the 33rd annual meeting of the association for computational linguistics, pp 189-196, doi: 10.3115/981658.981684

• 1998
  • Standard Co-training (Co-Training)

    Blum A, Mitchell T (1998) Combining labeled and unlabeled data with co-training. In: Proceedings of the annual ACM conference on computational learning theory, pp 92-100, doi: 10.1145/279943.279962

• 2000
  • Statistical co-learning (Statistical-Co)

    Goldman S, Zhou Y (2000) Enhancing supervised learning with unlabeled data. In: Proceedings of the 17th international conference on machine learning. Morgan Kaufmann, pp 327-334

     

• 2002
  • ASSEMBLE

    Bennett K, Demiriz A, Maclin R (2002) Exploiting unlabeled data in ensemble methods. In: Proceedings of the ACM SIGKDD international conference on knowledge discovery and data mining, pp 289-296, doi: 10.1145/775047.775090

• 2004
  • Democratic co-learning (Democratic-Co)

    Zhou Y, Goldman S (2004) Democratic co-learning. In: IEEE international conference on tools with artificial intelligence, pp 594-602, doi: 10.1109/ICTAI.2004.48

• 2005
  • Self-training with editing (SETRED)

    Li M, Zhou ZH (2005) SETRED: self-training with editing. In: Lecture notes in computer science (including subseries lecture notes in artificial intelligence and lecture notes in bioinformatics), vol 3518 LNAI, pp 611-621, doi: 10.1007/11430919_71

  • Tri-training (Tri-training)

    Zhou ZH, Li M (2005) Tri-training: exploiting unlabeled data using three classifiers. IEEE Trans Knowl Data Eng 17:1529-1541, doi: 10.1109/TKDE.2005.186

• 2006
  • Tri-training with editing (DE-TriTraining)

    Deng C, Guo M (2006) Tri-training and data editing based semi-supervised clustering algorithm. In: Gelbukh A, Reyes-Garcia C (eds) MICAI 2006: advances in artificial intelligence, vol 4293 of lecture notes in computer science. Springer, Berlin, pp 641-651, doi: 10.1007/11925231_61

• 2007
  • Co-forest (Co-forest)

    Li M, Zhou ZH (2007) Improve computer-aided diagnosis with machine learning techniques using undiagnosed samples. IEEE Trans Syst Man Cybern A Syst Hum 37(6):1088-1098, doi: 10.1109/TSMCA.2007.904745

• 2008
  • Random subspace method for co-training (Rasco)

    Wang J, Luo S, Zeng X (2008) A random subspace method for co-training. In: IEEE international joint conference on computational intelligence, pp 195-200, doi: 10.1109/IJCNN.2008.4633789

  • Co-training by committee: AdaBoost (Co-Adaboost)

    Hady M, Schwenker F (2008) Co-training by committee: a new semi-supervised learning framework. In: IEEE international conference on data mining workshops, ICDMW ’08, pp 563-572, doi: 10.1109/ICDMW.2008.27

• 2010
  • Co-training by committee: bagging (Co-Bagging)

    Hady M, Schwenker F (2010) Combining committee-based semi-supervised learning and active learning. J Comput Sci Technol 25:681-698, doi: 10.1109/IJCNN.2008.4633789

  • Co-training by committee: AdaBoost (Co-Adaboost)

    Hady M, Schwenker F (2010) Combining committee-based semi-supervised learning and active learning. J Comput Sci Technol 25:681-698, doi: 10.1109/IJCNN.2008.4633789

  • Co-training by committee: RSM (Co-RSM)

    Hady M, Schwenker F (2010) Combining committee-based semi-supervised learning and active learning. J Comput Sci Technol 25:681-698, doi: 10.1109/IJCNN.2008.4633789

  • Co-training by committed: Tree-structured ensemble (Co-Tree)

    Hady M, Schwenker F, Palm G (2010) Semi-supervised learning for tree-structured ensembles of rbf networks with co-training. Neural Netw 23:497-509, doi: 10.1016/j.neunet.2009.09.001

  • Co-training with relevant random subspaces (Rel-Rasco)

    Yaslan Y, Cataltepe Z (2010) Co-training with relevant random subspaces. Neurocomputing 73(10-12):1652-1661, doi: 10.1016/j.neucom.2010.01.018

  • Classification algorithm based on local clusters centers (CLCC)

    Huang T, Yu Y, Guo G, Li K (2010) A classification algorithm based on local cluster centers with a few labeled training examples. Knowl-Based Syst 23(6):563-571, doi: 10.1016/j.knosys.2010.03.015

  • Ant-based semi-supervised classification (APSSC)

    Halder A, Ghosh S, Ghosh A (2010) Ant based semi-supervised classification. In: Proceedings of the 7th international conference on swarm intelligence, ANTS’10, Springer, Berlin, Heidelberg, pp 376-383, doi: 10.1007/978-3-642-15461-4_34

  • Self-training nearest neighbor rule using cut edges (SNNRCE)

    Wang Y, Xu X, Zhao H, Hua Z (2010) Semi-supervised learning based on nearest neighbor rule and cut edges. Knowl-Based Syst 23(6):547-554, doi: 10.1016/j.knosys.2010.03.012

• 2011
  • Robust co-training (R-Co-Training)

    Sun S, Jin F (2011) Robust co-training. Int J Pattern Recognit Artif Intell 25(07):1113-1126.

  • Adaptive co-forest editing (ADE-CoForest)

    Deng C, Guo M (2011) A new co-training-style random forest for computer aided diagnosis. J Intell Inf Syst 36:253-281, doi:10.1007/s10844-009-0105-8

  • Co-training with NB and SVM classifiers (Co-NB-SVM)

    Jiang Z, Zhang S, Zeng J (2013) A hybrid generative/discriminative method for semi-supervised classification. Knowl-Based Syst 37:137-145, doi:10.1016/j.knosys.2012.07.020

• 2014
  • Self-Training Filtered

    I. Triguero, J.A. Saez, J. Luengo, S. Garcia, F. Herrera ,On the Characterization of Noise Filters for Self-Training Semi-Supervised in Nearest Neighbor Classification, Neurocomputing 132 (2014) 30-41, doi: 10.1016/j.neucom.2013.05.055

  • Synthetic Examples Generation for Self-Labeled Semi-Supervised Classification (SEG-SSC)

    I. Triguero, S. Garcia, F. Herrera , SEG-SSC: A Framework based on Synthetic Examples Generation for Self-Labeled Semi-Supervised Classification, IEEE Transactions on Cybernetics, doi: 10.1109/TCYB.2014.2332003

Experimental Analyses

Comparative analyses regarding the most popular Self-Labeled methods are provided in this section. They have been taken from the SCI2 survey on Self-Labeling (I. Triguero, S. García, F. Herrera, Self-Labeled Techniques for Semi-Supervised Learning: Taxonomy, Software and Empirical Study. Knowledge and Information Systems, doi: 10.1007/s10115-013-0706-y, in press (2014)). The data sets, parameters, and the rest of features of the experimental study are described at the survey complementary web page.

Results obtained

Labeled Ratio	xls file	ods file
10%
20%
30%
40%

Other Approaches to tackle Semi-Supervised Classification

Nowadays, the use of unlabeled data in conjunction with labeled data is a growing field in different research lines. Self-labeled techniques form a feasible and promising group to make use of both kinds of data, which is closely related to other methods.

Generative models

The first attempts to deal with unlabeled data correspond to this area that is also denoted as Cluster-then-Label methods. It includes those methods that assume a joint probability model p(x,y)=p(y)p(x|y), where p(x|y) is an identifiable mixture distribution, for example a Gaussian mixture model. Hence it follows a determined parametric model \cite{nigam00} using both unlabeled and labeled data. Cluster-then-label methods are closely related to generative models. Instead of using a probabilistic model, they apply a previous clustering step to the whole data set, and then they label each cluster with the help of labeled data.

A highly relevant reference for this topic is:

Nigam, K. and Mccallum, A.K. and Thrun, S. and Mitchell, T. Text classification from labeled and unlabeled documents using EM.
Machine Learning , 39(2):103-134 (2000)

Abstract: This paper shows that the accuracy of learned text classifiers can be improved by augmenting a small number of labeled training documents with a large pool of unlabeled documents. This is important because in many text classification problems obtaining training labels is expensive, while large quantities of unlabeled documents are readily available. We introduce an algorithm for learning from labeled and unlabeled documents based on the combination of Expectation-Maximization (EM) and a naive Bayes classifier. The algorithm first trains a classifier using the available labeled documents, and probabilistically labels the unlabeled documents. It then trains a new classifier using the labels for all the documents, and iterates to convergence. This basic EM procedure works well when the data conform to the generative assumptions of the model. However these assumptions are often violated in practice, and poor performance can result. We present two extensions to the algorithm that improve classification accuracy under these conditions: (1) a weighting factor to modulate the contribution of the unlabeled data, and (2) the use of multiple mixture components per class. Experimental results, obtained using text from three different real-world tasks, show that the use of unlabeled data reduces classification error by up to 30%.

 

Recent advances in these topics are:

Fujino A, Ueda N, Saito K, Semisupervised learning for a hybrid generative/discriminative classifier based on the maximum entropy principle.
IEEE Trans Pattern Anal Mach Intell , 30(3):424-437 (2008)

Abstract: This paper presents a method for designing semisupervised classifiers trained on labeled and unlabeled samples. We focus on a probabilistic semisupervised classifier design for multiclass and single-labeled classification problems and propose a hybrid approach that takes advantage of generative and discriminative approaches. In our approach, we first consider a generative model trained by using labeled samples and introduce a bias correction model, where these models belong to the same model family but have different parameters. Then, we construct a hybrid classifier by combining these models based on the maximum entropy principle. To enable us to apply our hybrid approach to text classification problems, we employed naive Bayes models as the generative and bias correction models. Our experimental results for four text data sets confirmed that the generalization ability of our hybrid classifier was much improved by using a large number of unlabeled samples for training when there were too few labeled samples to obtain good performance. We also confirmed that our hybrid approach significantly outperformed the generative and discriminative approaches when the performance of the generative and discriminative approaches was comparable. Moreover, we examined the performance of our hybrid classifier when the labeled and unlabeled data distributions were different.

 

Tang X-L, Han M Semi-supervised Bayesian artmap.
Appl Intell, 33(3):302-317 (2010)

Abstract: This paper proposes a semi-supervised Bayesian ARTMAP (SSBA) which integrates the advantages of both Bayesian ARTMAP (BA) and Expectation Maximization (EM) algorithm. SSBA adopts the training framework of BA, which makes SSBA adaptively generate categories to represent the distribution of both labeled and unlabeled training samples without any user’s intervention. In addition, SSBA employs EM algorithm to adjust its parameters, which realizes the soft assignment of training samples to cat- egories instead of the hard assignment such as winner takes all. Experimental results on benchmark and real world data sets indicate that the proposed SSBA achieves significantly improved performance compared with BA and EM-based semi-supervised learning method; SSBA is appropriate for semi-supervised classification tasks with large amount of unlabeled samples or with strict demands for classification accuracy.

Graph-based

This represents the SSC problem as a graph min-cut problem. Labeled and unlabeled examples constitute the graph nodes and the similarity measurements between nodes correspond to the graph edges. The graph construction determines the behavior of this kind of algorithm. These methods usually assume label smoothness over the graph. Its main characteristics are: nonparametric, discriminative and transductive in nature. A highly relevant reference for this topic is:

A. Blum and S. Chawla Learning from Labeled and Unlabeled Data using Graph Mincuts.
Proceedings of the Eighteenth International Conference on Machine Learning , 19-26 (2001)

Abstract: Many application domains suffer from not having enough labeled training data for learning. However, large amounts of unlabeled examples can often be gathered cheaply. As a result, there has been a great deal of work in recent years on how unlabeled data can be used to aid classification. We consider an algorithm based on finding minimum cuts in graphs, that uses pairwise relationships among the examples in order to learn from both labeled and unlabeled data.

 

Recent advances in these topics are:

Xie, B. and Wang, M. and Tao, D. Toward the optimization of normalized graph Laplacian.
IEEE Transactions on Neural Networks , 22(4) 660-666 (2011)

Abstract: Normalized graph Laplacian has been widely used in many practical machine learning algorithms, e.g., spectral clustering and semisupervised learning. However, all of them use the Euclidean distance to construct the graph Laplacian, which does not necessarily reflect the inherent distribution of the data. In this brief, we propose a method to directly optimize the normalized graph Laplacian by using pairwise constraints. The learned graph is consistent with equivalence and nonequivalence pairwise relationships, and thus it can better represent similarity between samples. Meanwhile, our approach, unlike metric learning, automatically determines the scale factor during the optimization. The learned normalized Laplacian matrix can be directly applied in spectral clustering and semisupervised learning algorithms. Comprehensive experiments demonstrate the effectiveness of the proposed approach.

 

Wang, J. and Jebara, T. and Chang, S.-F. Semi-supervised learning using greedy max-cut.
Journal of Machine Learning Research , 14(1) 771-800 (2013)

Abstract: Graph-based semi-supervised learning (SSL) methods play an increasingly important role in practical machine learning systems, particularly in agnostic settings when no parametric information or other prior knowledge is available about the data distribution. Given the constructed graph represented by a weight matrix, transductive inference is used to propagate known labels to predict the values of all unlabeled vertices. Designing a robust label diffusion algorithm for such graphs is a widely studied problem and various methods have recently been suggested. Many of these can be formalized as regularized function estimation through the minimization of a quadratic cost. However, most existing label diffusion methods minimize a univariate cost with the classification function as the only variable of interest. Since the observed labels seed the diffusion process, such univariate frameworks are extremely sensitive to the initial label choice and any label noise. To alleviate the dependency on the initial observed labels, this article proposes a bivariate formulation for graph-based SSL, where both the binary label information and a continuous classification function are arguments of the optimization. This bivariate formulation is shown to be equivalent to a linearly constrained Max-Cut problem. Finally an efficient solution via greedy gradient Max-Cut (GGMC) is derived which gradually assigns unlabeled vertices to each class with minimum connectivity. Once convergence guarantees are established, this greedy Max-Cut based SSL is applied on both artificial and standard benchmark data sets where it obtains superior classification accuracy compared to existing state-of-the-art SSL methods. Moreover, GGMC shows robustness with respect to the graph construction method and maintains high accuracy over extensive experiments with various edge linking and weighting schemes.

Semi-supervised support vector machines

S³VM is an extension of standard Support Vector Machines (SVM) with unlabeled data. This approach implements the cluster-assumption for SSL, that is, examples in data cluster have similar labels, so classes are well-separated and do not cut through dense unlabeled data. This methodology is also known as transductive SVM, although it learns an inductive rule defined over the search space.

A highly relevant reference for this topic is:

Chapelle, O. and Sindhwani, V. and Keerthi, S. S. Optimization Techniques for Semi-Supervised Support Vector Machines.
Journal of Machine Learning Research , 9 203--233 (2018)

Abstract: Due to its wide applicability, the problem of semi-supervised classification is attracting increasing attention in machine learning. Semi-Supervised Support Vector Machines (S3VMs) are based on applying the margin maximization principle to both labeled and unlabeled examples. Unlike SVMs, their formulation leads to a non-convex optimization problem. A suite of algorithms have recently been proposed for solving S3VMs. This paper reviews key ideas in this literature. The performance and behavior of various S3VMs algorithms is studied together, under a common experimental setting.

 

Advanced works in S³VM are:

Adankon, M. and Cheriet, M. Genetic algorithm-based training for semi-supervised SVM.
Neural Computing and Applications , 19(8) 1197-1206 (2010)

Abstract: The Support Vector Machine (SVM) is an interesting classifier with excellent power of generalization. In this paper, we consider applying the SVM to semi-supervised learning. We propose using an additional criterion with the standard formulation of the semi-supervised SVM (S 3 VM) to reinforce classifier regularization. Since, we deal with nonconvex and combinatorial problem, we use a genetic algorithm to optimize the objective function. Furthermore, we design the specific genetic operators and certain heuristics in order to improve the optimization task. We tested our algorithm on both artificial and real data and found that it gives promising results in comparison with classical optimization techniques proposed in literature.

 

Tian, X. and Gasso, G. and Canu, S. A multiple kernel framework for inductive semi-supervised SVM learning
Neurocomputing , 90 46-58 (2012)

Abstract: We investigate the benefit of combining both cluster assumption and manifold assumption underlying most of the semi-supervised algorithms using the flexibility and the efficiency of multiple kernel learning. The multiple kernel version of Transductive SVM (a cluster assumption based approach) is proposed and it is solved based on DC (Difference of Convex functions) programming. Promising results on benchmark data sets and the BCI data analysis suggest and support the effectiveness of proposed work.

Other problems connected with Semi-supervised Classification

Semi-supervised Clustering

This problem, also known as constrained clustering, aims to obtain better defined clusters than the ones obtained from unlabeled data. Labeled data is used to define pairwise constraints between examples, must-links and cannot-links. The former link establishes the examples which must be in the same cluster, the latter refers to those examples that cannot be in the same cluster \cite{yin10}.
A brief review of this topic can be found in

N. Grira and M. Crucianu and N. Boujemaa Unsupervised and Semi-supervised Clustering: A Brief Survey
Report of the MUSCLE European Network of Excellence , (2014)

Abstract: Clustering (or cluster analysis) aims to organize a collection of data items into clusters, such that items within a cluster are more \similar" to each other than they are to items in the other clusters. This notion of similarity can be expressed in very dierent ways, according to the purpose of the study, to domain-speci c assumptions and to prior knowledge of the problem. Clustering is usually performed when no information is available concerning the membership of data items to prede ned classes. For this reason, clustering is traditionally seen as part of unsupervised learning. We nevertheless speak here of unsupervised clustering to distinguish it from a more recent and less common approach that makes use of a small amount of supervision to \guide" or \adjust" clustering (see section 2). To support the extensive use of clustering in computer vision, pattern recognition, information retrieval, data mining, etc., very many dierent methods were developed in several communities. Detailed surveys of this domain can be found in [24], [26] or [25]. In the following, we attempt to brie y review a few core concepts of cluster analysis and describe categories of clustering methods that are best represented in the literature. We also take this opportunity to provide some pointers to more recent work on clustering.

Active Learning

With the same objective as SSL, avoiding the cost of data labeling, active learning tries to select the most important examples from a pool of unlabeled data. These examples are queried by an expert, and are then labeled with the appropriate class, aiming to minimize effort and time-consumption. Many active learning algorithms select as query the examples with maximum label ambiguity or least confidence. Several hybrid methods between self-labeled techniques and active learning have been proposed, and show that active learning queries maximize the generalization capabilities of SSL. One oustanding reference of this field is:

Freund, Y. and Seung, H. S. and Shamir, E. and Tishby, N. Selective Sampling Using the Query by Committee Algorithm
Machine Learning,28 133-168 (1997)

Abstract: We analyze the ''query by committee'' algorithm, a method for filtering informative queries from a random stream of inputs. We show that if the two-member committee algorithm achieves information gain with positive lower bound, then the prediction error decreases exponentially with the number of queries. We show that, in particular, this exponential decrease holds for query learning of perceptrons.

Semi-Supervised Dimensionality Reduction

This area studies the curse of dimensionality when it is addressed in an SSL framework. The goal of dimensionality reduction algorithms is to find a faithful low dimensional mapping, or selection, of the high dimensional data. Traditional dimensionality reduction techniques designed for supervised and unsupervised learning, such as linear discriminant analysis and principal component analysis, are not appropriate to deal with both labeled and unlabeled data. Different frameworks have been proposed to use classical methods in this environment. A representative example of this topic is:

Song, Y. and Nie, F. and Zhang, C. and Xiang, S A unified framework for semi-supervised dimensionality reduction
Pattern Recognition, 41 2789-2799 (2008)

Abstract: In practice, many applications require a dimensionality reduction method to deal with the partially labeled problem. In this paper, we propose a semi-supervised dimensionality reduction framework, which can efficiently handle the unlabeled data. Under the framework, several classical methods, such as principal component analysis (PCA), linear discriminant analysis (LDA), maximum margin criterion (MMC), locality preserving projections (LPP) and their corresponding kernel versions can be seen as special cases. For high-dimensional data, we can give a low-dimensional embedding result for both discriminating multi-class sub-manifolds and preserving local manifold structure. Experiments show that our algorithms can significantly improve the accuracy rates of the corresponding supervised and unsupervised approaches.

Self-Supervised

This paradigm integrates knowledge from labeled data with some features and knowledge from unlabeled data with all the features. Thus, self-supervised algorithms learn novel features from unlabeled examples without destroying partial knowledge previously acquired from labeled examples. This paradigm was initially presented in:

Gregory, P. A. and Gail, A. C. Self-supervised ARTMAP
Neural Networks, 23 265-282 (2010)

Abstract: Computational models of learning typically train on labeled input patterns (supervised learning), unlabeled input patterns (unsupervised learning), or a combination of the two (semi-supervised learning). In each case input patterns have a fixed number of features throughout training and testing. Human and machine learning contexts present additional opportunities for expanding incomplete knowledge from formal training, via self-directed learning that incorporates features not previously experienced. This article defines a new self-supervised learning paradigm to address these richer learning contexts, introducing a neural network called self-supervised ARTMAP. Self-supervised learning integrates knowledge from a teacher (labeled patterns with some features), knowledge from the environment (unlabeled patterns with more features), and knowledge from internal model activation (self-labeled patterns). Self-supervised ARTMAP learns about novel features from unlabeled patterns without destroying partial knowledge previously acquired from labeled patterns. A category selection function bases system predictions on known features, and distributed network activation scales unlabeled learning to prediction confidence. Slow distributed learning on unlabeled patterns focuses on novel features and confident predictions, defining classification boundaries that were ambiguous in the labeled patterns. Self-supervised ARTMAP improves test accuracy on illustrative low-dimensional problems and on high-dimensional benchmarks. Model code and benchmark data are available from: http://techlab.eu.edu/SSART/.

Partial Label

This problem deals with partially-labeled multi-class classification, in which instead of a single label per instance, it has a candidate set of labels, only one of which is correct. In these circumstances, a classifier should learn how to disambiguate the partially-labeled training instance and generalize to unseen data. It was proposed in

Cour, T. and Sapp, B. and Taskar, B. Learning from partial labels
Journal of Machine Learning Research, 12 1501-1536 (2012)

Abstract: We address the problem of partially-labeled multiclass classification, where instead of a single label per instance, the algorithm is given a candidate set of labels, only one of which is correct. Our setting is motivated by a common scenario in many image and video collections, where only partial access to labels is available. The goal is to learn a classifier that can disambiguate the partially-labeled training instances, and generalize to unseen data. We define an intuitive property of the data distribution that sharply characterizes the ability to learn in this setting and show that effective learning is possible even when all the data is only partially labeled. Exploiting this property of the data, we propose a convex learning formulation based on minimization of a loss function appropriate for the partial label setting. We analyze the conditions under which our loss function is asymptotically consistent, as well as its generalization and transductive performance. We apply our framework to identifying faces culled from web news sources and to naming characters in TV series and movies; in particular, we annotated and experimented on a very large video data set and achieve 6% error for character naming on 16 episodes of the TV series Lost.

The impact of Semi-Supervised Classification

The ISI Web of Science provides seamless access to current and retrospective multidisciplinary information from approximately 8,700 of the most prestigious, high impact research journals in the world. The web of Science also provides a unique search method, cited reference searching. With it, users can navigate forward, backward, and through the literature, searching all disciplines and time spans to uncover all the information relevant to their research. Users can also navigate to electronic full-text journal articles (http://scientific.thomson.com/products/wos/).

In the link of "Advanced Search", we consider the following query, using SSC as a 'Topic' field for the search:

SSC= ("Semi-Supervised classification" OR "Semisupervised classification" OR ("Semi-supervised learning" AND "classification") OR ("Semisupervised learning" AND "classification"))

The numerical results of the query are:

Date of analysis: July 16th, 2014
Number of papers: 1234
Sum of the times cited: 6650
Average citations per item: 5.39

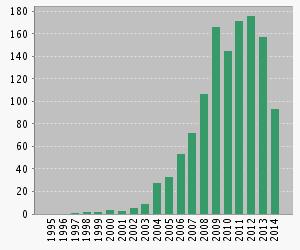
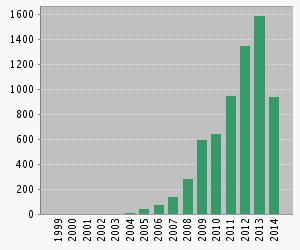
Figures 2 and 3 show the number of publications and citations per year.

Fig. 2. Publications in SSC per year (Web of Science)	Fig. 3. Number of citations per year (Web of Science)

In these figures we can see that the SSC field is a promising topic in which more approaches are presented every year, aiming to improve the performance of the techniques developed so far.

Software, Algorithm Implementations and Dataset Repository

All algorithms selected for the experimental framework have been included into the KEEL software, under a specific module for semi-supervised classification. Additionally, KEEL contains a complete dataset repository in which all the problems used in this, and other related journal papers, are available for download. In this way, any interested researcher can use the same data partitions for comparison.

Knowledge Extraction based on Evolutionary Learning (KEEL): KEEL is a software tool to assess evolutionary algorithms for Data Mining problems including regression, classification, semi-supervised classification, clustering, pattern mining and so on. It contains a big collection of classical knowledge extraction algorithms, preprocessing techniques (instance selection, feature selection, discretization, imputation methods for missing values, etc.), Computational Intelligence based learning algorithms, including evolutionary rule learning algorithms based on different approaches (Pittsburgh, Michigan and IRL, ...), and hybrid models such as genetic fuzzy systems, evolutionary neural networks, etc. It allows us to perform a complete analysis of any learning model in comparison to existing ones, including a statistical test module for comparison. Moreover, KEEL has been designed with a double goal: research and educational. This software tool will be available as open source software this summer. For more information about this tool, please refer to the following publication:

 

• J. Alcalá-Fdez, L. Sánchez, S. García, M.J. del Jesus, S. Ventura, J.M. Garrell, J. Otero, C. Romero, J. Bacardit, V.M. Rivas, J.C. Fernández, F. Herrera, KEEL: A Software Tool to Assess Evolutionary Algorithms for Data Mining Problems. Soft Computing, 13:3 (2009) 307-318. doi: 10.1007/s00500-008-0323-y  ENLACE AL PDF ROTO

KEEL Data Set Repository (KEEL-dataset): KEEL-dataset repository is devoted to the data sets in KEEL format which can be used with the software and provides: A detailed categorization of the considered data sets and a description of their characteristics. Tables for the data sets in each category have been also created; A descriptions of the papers which have used the partitions of data sets available in the KEEL-dataset repository. These descriptions include results tables, the algorithms used and additional material. For more information about this repository, please refer to the following publication:

• J. Alcalá-Fdez, A. Fernández, J. Luengo, J. Derrac, S. García, L. Sánchez, F. Herrera , KEEL Data-Mining Software Tool: Data Set Repository, Integration of Algorithms and Experimental Analysis Framework. Journal of Multiple-Valued Logic and Soft Computing 17:2-3 (2011) 255-287.