A review of the application of Multi-Objective Evolutionary Fuzzy Systems: Current status and further directions
This web page contains additional material related to the following paper:
M. Fazzolari, R. Alcalá, Y. Nojima, H. Ishibuchi, F. Herrera. A review of the application of Multi-Objective Evolutionary Systems: Current status and further directions. IEEE Transactions on Fuzzy Systems 21(1) (2013) 45-65, doi: 10.1109/TFUZZ.2012.2201338 ![]()
- Paper content
- Complementary Material 1: Preliminaries
- Complementary Material 2: A taxonomy of contributions dealing with MOEFSs
- A summary of the application of MOEFSs for each main category: Contributions after paper publication (still not available)
Paper content
M. Fazzolari, R. Alcalá, Y. Nojima, H. Ishibuchi, F. Herrera. A review of the application of Multi-Objective Evolutionary Systems: Current status and further directions. IEEE Transactions on Fuzzy Systems 21(1) (2013) 45-65, doi: 10.1109/TFUZZ.2012.2201338 ![]()
Abstract: Over the past few decades, Fuzzy Systems have been widely used in several application fields, thanks to their ability to model complex systems. The design of fuzzy systems has been successfully performed by applying Evolutionary and, in particular, Genetic Algorithms, and recently, this approach has been extended by using Multiobjective Evolutionary Algorithms, which can consider multiple conflicting objectives, instead of a single one. The hybridization between Multiobjective Evolutionary Algorithms and Fuzzy Systems is currently known as Multiobjective Evolutionary Fuzzy Systems. This paper presents an overview of Multiobjective Evolutionary Fuzzy Systems, describing the main contributions on this field and providing a two-level taxonomy of the existing proposals, in order to outline a well-established framework that could help researchers who work on significant further developments. Finally, some considerations of recent trends and potential research directions are presented.
Summary:
- Introduction
- Taxonomy Based on the Application of Multiobjective Evolutionary Fuzzy Systems
- Multiobjective Evolutionary Fuzzy Systems Designed to Generate Fuzzy Rule-Based Systems with Different Accuracy-interpretability Tradeoffs
- Approaches to Performing Tuning
- Approaches to Performing KB Learning
- Approaches That Deal With TSK Fuzzy Rule-Based Systems
- Summary of Multiobjective Evolutionary Fuzzy Systems Designed to Generate Fuzzy Rule-Based Systems with Different Accuracy-Interpretability Tradeoffs
- Multiobjective Evolutionary Fuzzy Systems Designed for Multiobjective Control Problems
- Controller Parameters' Identification
- Learning of Controller Structure
- Summary of Multiobjective Evolutionary Fuzzy Systems Designed for Multiobjective Control Problems
- Multiobjective Evolutionary Fuzzy Systems Designed for Fuzzy Association Rule Mining
- Description of the Existent Contributions
- Summary of Multiobjective Evolutionary Fuzzy Systems Designed for Fuzzy Association Rule Mining
- Open Problems and New Trends in Multiobjective Evolutionary Fuzzy Systems
- Performance Evaluation of Multi-Objective Evolutionary Fuzzy Systems Approaches
- Reliable Interpretability Measures
- Objective Dimensionality
- Scalability Issues
- Imbalanced Datasets
- Automatic Selection of the Most Suitable Solution
- Integration of Decision Maker’s Preferences
- Design Multiobjective Evolutionary Fuzzy Systems to Generate Type-2 Fuzzy Systems
- Conclusion
Complementary Material 1: Preliminaries
This section introduces some basic concepts related to MOEFSs. Firstly, FRBSs are introduced. Secondly, some important concepts regarding evolutionary optimization techniques and particularly Evolutionary Multi-Objective Optimization (EMOO) techniques are presented. Finally MOEFSs are defined as the hybridization of the two approaches.
Fuzzy Rule-Based Systems
Fuzzy systems are one of the most important areas for the application of Fuzzy Set Theory, proposed by Lotfi Zadeh in 1965 (Zadeh L (1965) Fuzzy sets. Inf Control 8:338-353,![]() ). Fuzzy systems were applied at first in control engineering (Zadeh L (1973) Outline of a new approach to the analysis of complex systems and decision processes. IEEE Trans Syst Man Cybern SMC-3:28-44, doi: 10.1109/TSMC.1973.5408575) in the mid 1970s, when Mamdani proposed the first fuzzy controller (Mamdani E (1974) Application of fuzzy algorithms for control of simple dynamic plant. Proceedings of IEEE 121(12):1585-1588, doi: 10.1049/piee.1974.0328, Mamdani E, Assilian S (1975) An experiment in linguistic synthesis with a fuzzy logic controller. Int J Man Mach Stud 7(1):1-13, doi: 10.1016/S0020-7373(75)80002-2).
). Fuzzy systems were applied at first in control engineering (Zadeh L (1973) Outline of a new approach to the analysis of complex systems and decision processes. IEEE Trans Syst Man Cybern SMC-3:28-44, doi: 10.1109/TSMC.1973.5408575) in the mid 1970s, when Mamdani proposed the first fuzzy controller (Mamdani E (1974) Application of fuzzy algorithms for control of simple dynamic plant. Proceedings of IEEE 121(12):1585-1588, doi: 10.1049/piee.1974.0328, Mamdani E, Assilian S (1975) An experiment in linguistic synthesis with a fuzzy logic controller. Int J Man Mach Stud 7(1):1-13, doi: 10.1016/S0020-7373(75)80002-2).
The main feature of this approach is that it provides an approximate but effective means of describing the behavior of complex systems, thus avoiding the need for a precise mathematical model of the system to be controlled. Fuzzy systems have been extensively and successfully applied to several fields, such as economics, engineering, science, psychology, medicine etc.
The most common fuzzy system model consists of a collection of logical IF-THEN rules, whose antecedents and consequents are composed of fuzzy logic statements, related by the dual concepts of fuzzy implication and the compositional rule of inference. These kinds of systems are called FRBSs and are composed of a Knowledge Base (KB), which includes the information in the form of IF-THEN fuzzy rules, and an inference engine module.
Depending on the format of the rules, FRBSs can be roughly divided in several families, which differ in their ability to represent different types of information.
The two most popular FRBSs are linguistic fuzzy models, also called Mamdani-type (Mamdani E (1974) Application of fuzzy algorithms for control of simple dynamic plant. Proceedings of IEEE 121(12):1585-1588, doi: 10.1049/piee.1974.0328) and Takagi-Sugeno-Kang fuzzy models (Takagi T, Sugeno M (1985) Fuzzy identification of systems and its applications to modeling and control. IEEE Trans Syst Man Cybern 15(1):116-132, ![]() ).
).
In linguistic fuzzy models, the fuzzy quantities are associated with linguistic labels and the model is a qualitative expression of the system. This type of model describes the system behavior using a natural language. The consequent of the rule can be an output action or a class to be applied:
$$R_i: If X_1 is A_{i1} and ... and X_n is A_{in} then Y is B_i$$
or
$$R_i: If X_1 is A_{i1} and ... and X_n is A_{in} then C_i with w_i$$
with i=1 to M, $X_1$ to $X_n$ and Y being the input and output variables for regression respectively, $A_{i1} $to $A_{in}$ and $B_i$ being the involved antecedent and consequent labels respectively, $C_i$ being the output class associated to the rule for classification and $w_i$ being the certain factor associated to the class. These systems are usually called linguistic or Mamdani FRBSs.
TSK fuzzy models are composed of logical rules that have a fuzzy antecedent and functional consequent parts. They can be represented as:
$$R_i: If X_1 is A_{i1} and ... and X_n is A_{in} then Y=p(X_i,...,X_n)$$
with p(·) being a polynomial function, usually a linear expression:
$$Y=p_0+p_1·X_1+...+p_n·X_n$$
This approach approximates a non-linear system with a combination of several linear systems. TSK models are composed of logical rules that have a fuzzy antecedent and consequent without any associated linguistic meaning, i.e. comprised of free-semantic fuzzy members.
Another category of fuzzy models is represented by scatter partition-based FRBSs (Alcalá R, Casillas J, Cordón O, Herrera F (2001) Building fuzzy graphs: features and taxonomy of learning for non-grid-oriented fuzzy rule-based systems. J. Intell. Fuzzy Syst. 11:99-119, ![]() ), which differ from linguistic FRBSs because of their semantic-free rules. Each fuzzy rule presents its own semantic, i.e., the variables take different fuzzy sets as values (and not linguistic terms from a global term set). Therefore, the fuzzy rule structure is as follow:
), which differ from linguistic FRBSs because of their semantic-free rules. Each fuzzy rule presents its own semantic, i.e., the variables take different fuzzy sets as values (and not linguistic terms from a global term set). Therefore, the fuzzy rule structure is as follow:
$$R_i: If X_1 is \widehat{A_{i1}} and ... and X_n is \widehat{A_{in}} then Y is \widehat{I_i}$$
with $\widehat{A_{i1}}$ to $\widehat{A_{in}}$ and $\widehat{I_i}$ being fuzzy sets.
In the case of linguistic variables, the KB includes two components, a Rule Base (RB) and a Data Base (DB):
- the RB contains a set of IF-THEN fuzzy rules, which are joined by a rule connective ("or" operator), therefore the same input can fire multiple rules concurrently;
- the DB includes the fuzzy sets associated with the linguistic terms of the RB.
Each linguistic variable involved in the problem is defined over a universe U and is associated to a fuzzy partition, which represents a set of linguistic terms. Linguistic terms are associated to fuzzy sets, which are the values that a linguistic variable can assume. The number of fuzzy sets in a fuzzy partition can be variable and is called granularity. The determination of fuzzy partitions is essential in fuzzy modeling since the granularity of fuzzy partitions strongly affects the performance of FRBSs, in regression and classification problems.
The inference engine module of FRBSs is defined in different ways, depending on the kind of problem (classification or regression) and the kind of fuzzy rules. It is always constituted by three elements:
- a fuzzification interface, which transforms crisp data into fuzzy sets;
- an inference system, which uses fuzzy sets together with the KB to make inferences by means of a reasoning method;
- defuzzification interface, which uses a defuzzification method in order to translate the obtained fuzzy sets into a crisp action, in the case of regression problems, or to provide the final class associated to an input pattern, in the case of classification problems.
The generic structure of an FRBS is shown in Figure 1. A detailed description of FRBSs can be found in the following books: Wang LX (1994) Adaptive Fuzzy Systems and Control: Design and Stability Analysis. Prentice-Hall, Upper Saddle River, NJ, USA, Bardossy A, Duckstein L (1995) Fuzzy Rule-Based Modeling with Applications to Geophysical, Biological, and Engineering Systems. CRC Press, Boca Raton, Florida, USA, Driankov D, Hellendoorn H, Reinfrank M (1996) An Introduction to Fuzzy Control, 2nd edn. Springer-Verlag, London.
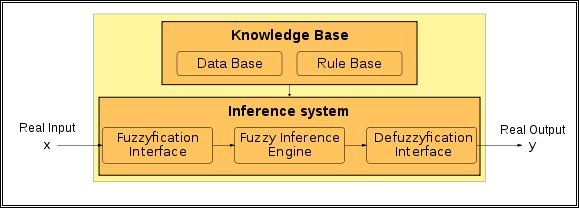
Figure 1: Structure of an FRBS.
Evolutionary Multi-Objective Optimization (EMOO)
The origin of evolutionary algorithms can be traced back to the 1950's. Genetic algorithms, evolution strategies and evolutionary programming are three main approaches to evolutionary computation. Genetic algorithms (Goldberg DE (1989) Genetic Algorithms in Search, Optimization, and Machine Learning. Addison-Wesley, Boston, Massachussets, USA, Holland JH (1992) Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence. The MIT Press) are general purpose search algorithms that use principles inspired by natural genetic populations to evolve solutions to problems. The basic idea is to maintain a population of individuals that evolves over time through a process of competition and cooperation. Each individual constitutes a candidate solution to a problem and has an associated fitness, which represents the quality of the solution. New solutions are created by means of genetic operators such as crossover and mutation. Genetic algorithms have been successfully used in various applications of search and optimization problems.
Multi-objective problem
Even though some real problems can be described by means of a single objective, there are cases in which it is difficult to define all the aspects in terms of a single objective. For this reason multi-objective optimization has become very popular in the last few years and its application is continuously increasing (Deb K, (2001) Multi-Objective Optimization Using Evolutionary Algorithms. John Wiley & Sons, Inc., New York, USA , Coello CAC, Lamont GB, Veldhuizen DAV (2006) Evolutionary Algorithms for Solving Multi-Objective Problems (Genetic and Evolutionary Computation). Springer-Verlag, Secaucus, NJ, USA). A considerable amount of papers and books has been published in this research area, now named EMOO. In the following subsections, some well-known concepts regarding EMOO will be briefly introduced. First, a multi-objective problem is described by means of mathematical equations, then the definitions of Pareto optimal and Pareto front are explained. Finally, a quick overview of the most important MOEAs is provided.
Multi-objective optimization usually involves multiple contradictory objectives to be optimized simultaneously, thus there is no longer a single optimal solution but rather a set of feasible solutions of equivalent quality and each solution represents a trade-off between the conflicting objectives.
The problem can be formally formulated as follows: find the vector
$$\bar{x}^*=[x_1^*,x_2^*,...,x_n^*]^T$$
which will satisfy the m inequality constraints:
$$g_i(\bar{x}) \ge 0 i=1,2,...,m$$
the p equality constraints:
$$h_i(\bar{x}) = 0 i=1,2,...,p$$
and minimizes the vector function
$$\bar{f}(\bar{x}) = [f_1(\bar{x}),f_2(\bar{x}),...,f_k(\bar{x})]^T$$
where $\bar{x}=[x_1,x_2,...,x_n]^T \ is \ the \ vector \ of \ decision \ variables.$
Pareto optimal and Pareto front definitions
The concept of Pareto optimal was stated in the 19th century by Pareto (Pareto V (1896) Cours d'economie politique. F. Rouge, Lausanne) and constitutes the origin of research in multi-objective optimization. A solution $\bar{x}^*$ is Pareto optimal if it is not dominated within the entire search space, that is, if for every $$\bar{x} either
$$f_i(\bar{x})=f_i(\bar{x}^*) ∀i \in 1,...,I$$
where I is the number of objectives, or there is at least one i \in I so that
$$f_i(bar{x}) > f_i(bar{x}^*)$$
Therefore, a solution $\bar{x}^*$ is Pareto optimal if there is no feasible vector $\bar{x}$ which would decrease some criterion without causing at the same time an increase in at least one other criterion. The set of all Pareto optimal solutions is denoted as Pareto optimal set and the corresponding objective vectors form the Pareto front. Thus, the aim of a multi-objective optimization algorithm is to find a family of solutions that are a good approximation of the Pareto front.
Multi-Objective Evolutionary Algorithms
Evolutionary algorithms simultaneously deal with a set of possible solutions (the so-called population) and are able to find several members of the Pareto optimal set in a single run of the algorithm. Additionally, they are not too susceptible to the shape or continuity of the Pareto front, e.g. they can easily deal with discontinuous and concave Pareto fronts. The possibility of using evolutionary-based searches to deal with multiple objectives was suggested for the first time by Rosenberg (Rosenberg R (1967) Simulation of genetic populations with biochemical properties. PhD thesis, Univ. Michigan) in his Ph.D. thesis, although no MOEA was developed in it: the multi-objective problem was restated as a single-objective problem and solved with a genetic algorithm.
The first implementation of an MOEA was the Vector Evaluation Genetic Algorithm (VEGA) (Schaffer JD (1985) Multiple objective optimization with vector evaluated genetic algorithms. In Proceedings of the 1st International Conference on Genetic Algorithms, 93-100) proposed by Schaffer. Despite its simplicity, the algorithm suffers from some drawbacks. After VEGA, several algorithms were designed, mainly characterized by their simplicity. In 1989 Goldberg (Goldberg DE (1989) Genetic Algorithms in Search, Optimization, and Machine Learning. Addison-Wesley, Boston, Massachussets, USA) suggested combining a good mechanism to select non-dominated individuals (perhaps, but not necessarily, based on the concept of Pareto optimality) with some mechanism to maintain diversity (fitness sharing was a choice, but not the only one), in order to achieve a selective pressure toward the non-dominated front while maintaining at the same time diversity along the front. These two concepts were widely exploited in the first generation of MOEAs. The most representative MOEAs of this generation are the following: Non-dominated Sorting Genetic Algorithm (NSGA), Niched-Pareto Genetic Algorithm (NPGA), Multi-Objective Genetic Algorithm (MOGA) and Multi-Objective Genetic Local Search (MOGLS).
In the second generation of MOEAs, the concept of elitism was introduced, since it is a theoretical requirement in order to guarantee the convergence of an MOEA (Rudolph G, Agapie A (2000) Convergence properties of some multi-objective evolutionary algorithms. In Proceedings of the 2000 Congress on Evolutionary Computation, vol. 2, 1010-1016). Elitism refers to the use of an external population to store the non-dominated individuals found so far in the optimization process. Elitism can also be introduced by using a different selection process, in which parents compete with their children for the selection of the non-dominated solutions that will be included the following generation. Many MOEAs have been proposed during the second generation, but only a few algorithms are considered to be paradigms by researchers. The most representative MOEAs of the second generation are the Strength Pareto Evolutionary Algorithm (SPEA) and its evolution SPEA2, the Pareto Archived Evolution Strategy (PAES), the Pareto Envelope-based Selection Algorithm (PESA) and PESA2, the micro-GA and its improvement, NPGA2 and finally NSGA-II.
NSGA-II is the current paradigm in the MOEA research community, because it can usually obtain the widest Pareto sets in many problems, although recently researchers have been looking for new algorithms that could manage many objectives or very complex Pareto fronts, by controlling population density in a more effective way. Among them, the most famous one is the Multi-Objective Evolutionary Algorithm based on Decomposition (MOEA/D). Table 1 shows a summary of the most representative MOEAs of both generations.
Table 1. Classification of MOEAs.
| Name | Year | 1st generation | 2nd generation |
|---|---|---|---|
| MOGA | 1993 | ✓ | |
| NPGA | 1994 | ✓ | |
| NSGA | 1994 | ✓ | |
| MOGLS | 1996 | ✓ | |
| SPEA, SPEA2 | 1999, 2001 | ✓ | |
| PAES | 2000 | ✓ | |
| PESA, PESA-II | 2000, 2001 | ✓ | |
| micro-GA, micro-GA 2 | 2001, 2003 | ✓ | |
| NPGA 2 | 2001 | ✓ | |
| NSGA-II | 2002 | ✓ | |
| MOEA/D | 2007 | ✓ | |
| MODdEA | 2011 | ✓ |
Researchers are still looking for new characteristics that will give rise to the third generation. They seem to be oriented towards many-objective optimization, since it is known that more than three objectives are difficult to handle (Ishibuchi H, Tsukamoto N, Nojima Y (2008) Evolutionary many-objective optimization. In 3rd International Workshop on Genetic and Evolving Fuzzy Systems, 47-52, doi: 10.1109/GEFS.2008.4484566). Other research fields are algorithm efficiency and spatial data structures that improve the efficiency of storage in the external population.
Genetic Fuzzy Systems (GFSs) and Multi-Objective Evolutionary Fuzzy Systems (MOEFSs)
The automatic definition of a fuzzy system can be considered as an optimization or search problem. Since evolutionary algorithms, and particularly GAs, are known for their ability to solve optimization problems, they can be used to explore the search space of the acceptable solutions in order to find the optimal one. The hybridization between fuzzy systems and genetic algorithms brought to the so-called GFSs (Cordón O, Herrera F, Hoffmann F and Magdalena L (2001) Genetic Fuzzy Systems. Evolutionary Tuning and Learning of Fuzzy Knowledge Bases. World Scientific, Singapore, New Jersey, London, Hong Kong), (Cordón O, Gomide F, Herrera F, Hoffmann F, Magdalena L (2004) Ten years of genetic fuzzy systems: current framework and new trends. Fuzzy Sets Syst 141(1):5-31, doi: 10.1016/S0165-0114(03)00111-8) (Herrera F (2008) Genetic fuzzy systems: taxonomy, current research trends and prospects. Evol Intell 1:27-46, doi: 10.1007/s12065-007-0001-5). A detailed description of GFSs can be found here.
A GFS is a fuzzy system in which system parameters or structures are evolved by means of a genetic algorithm. A genetic learning process covers different levels of complexity, i.e., it can be used for parameter optimization, to improve the performance of an existing fuzzy system, or for structural tasks, such as learning the whole rule set of a FRBS (Figure 2).
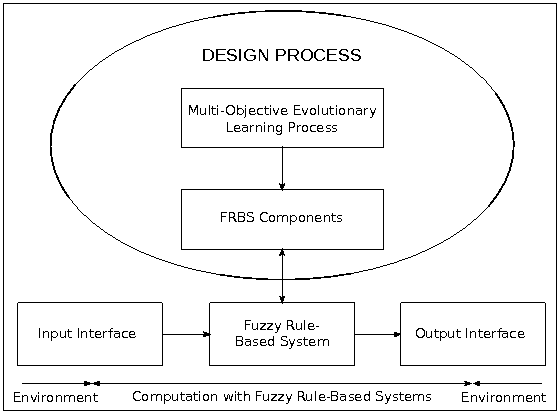
Figure 2: MOEFS design process.
Initially, GFSs were mainly used to design FRBSs with high accuracy in problems such as classification and control, but later on the need to include multiple objectives arose (Ishibuchi H, Murata T, Turksen IB (1997) Single-objective and two-objective genetic algorithms for selecting linguistic rules for pattern classification problems. Fuzzy Sets Syst 89(2):135-150, doi: 10.1016/S0165-0114(96)00098-X). As stated above, in a multi-objective problem objectives are often conflicting, thus a multi-objective evolutionary algorithm generates a set of fuzzy systems and each of them has a different trade-off between objectives. The chosen objectives depend on the aim of the designed fuzzy system. The primary one is the accuracy of the system with respect to a performance metric. Other objectives can be the complexity of the system, the cost, the computational time, additional performance metrics, etc. The application of MOEAs to learn or tune fuzzy systems brings about the MOEFSs.
Complementary Material 2: A taxonomy of contributions dealing with MOEFSs
Our proposal analyzes a collection of papers in which MOEFSs are applied to different problems. In this section a brief overview of the considered categories is given and then three summarizing tables are presented.
Proposed taxonomy
We propose a two-level taxonomy, as showed in figure 3, in order to jointly analyze the different types of MOEFSs. The first level gathers contributions depending on the multi-objective nature of the handled problem, i.e. the type of the objectives optimized. The second one groups papers depending on the type of FRBS components that are managed by the optimization process. In fact, both of them affect the type and the complexity of the search space, and therefore the way to apply MOEFSs:
- MOEFSs designed to generate FRBSs with different Accuracy-Interpretability trade-offs. In this case at least one of the objectives is always related to the interpretability of the obtained model, regardless of the problem considered. A considerable number of papers can be found in this group, since the interpretability is one of the most important aspects of FRBSs. While the accuracy is difficult to improve, the interpretability is easy to get, since interpretable models can be given even by hand. These differences between both types of objectives influence the optimization process.
- MOEFSs designed for multi-objective control problems. The considered objectives strictly depend on the particular kind of problem that is taken into account and usually all of them are related with performance issues of the control system. Therefore, the trade-off and the search space will be different and dependent on the problem itself.
- MOEFSs designed for Fuzzy Association Rule Mining. The aim of rule mining is to find a set of fuzzy association rules that reliably represents the knowledge hidden in a data base. In this case, the objectives are used to describe the quality of the obtained rules, i.e. their accuracy and interestingness. To this end, support and confidence are the major factors in measuring the quality of an association rule, but other metrics exists. The aim of the optimization process is not only to improve the general trade-off between objectives for the whole set of rules, but also to obtain a great number of rules, each of them satisfying the objectives at different degrees.
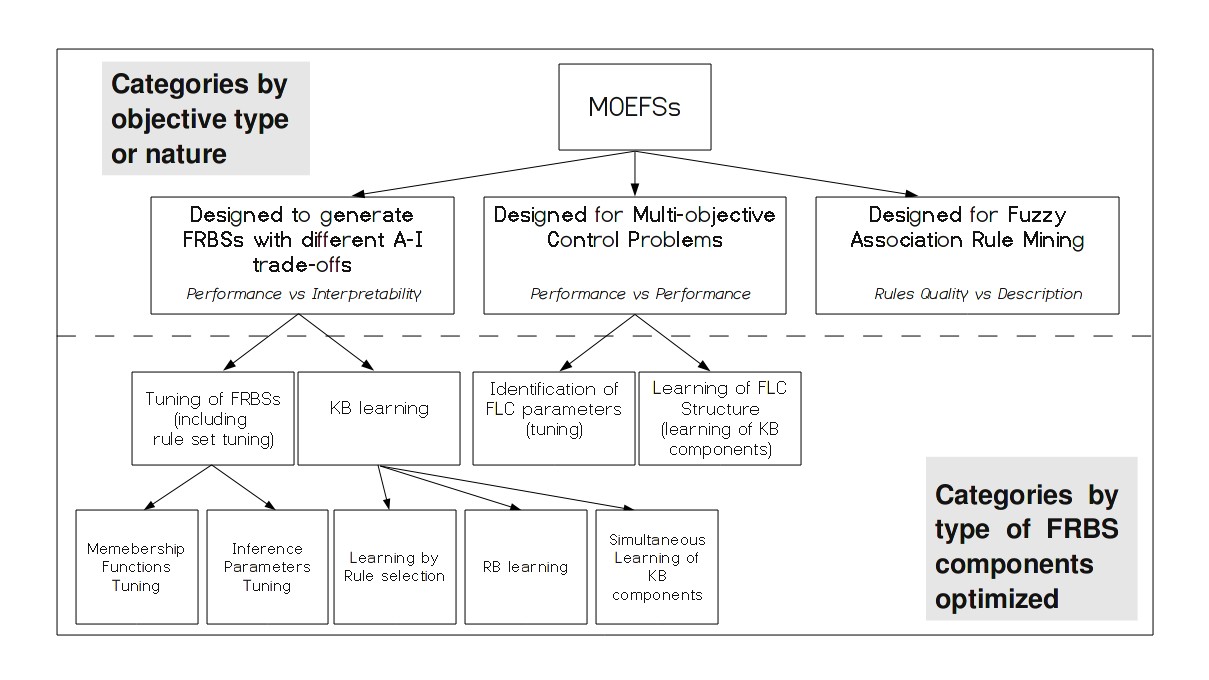
Figure 3: A two-level taxonomy based on the type of the objectives used (1st level) and on the type of FRBS components optimized (2nd level).
A summary of the contributions dealing with MOEFSs, with respect to each main category: Contributions in the paper (including DOI)
This section contains a visual summary of the proposed taxonomy. Contributions are presented in the form of tables so that all those related to a particular branch can be easily found.
MOEFSs designed to generate FRBSs with different Accuracy-Interpretability trade-offs
The following table presents a summary of the works on the use of MOEFSs to generate FRBSs with good Accuracy-Interpretability trade-offs. Papers are grouped considering the components of FRBS that are managed by the optimization process.
Table 2. Summary of proposals on MOEFSs designed to generate FRBSs with good Accuracy-Interpretability trade-offs.
tabla con formato diferente
| A-I trade-off | FRBS approach | Objectives | MOEA | ||||||||
| Authors | Year | Rules | Type | #Obj. | Type | Name | Gen. | Type | Problem type | ||
| Wang et al. | 2005 | TSK | Ling.* | 5 | A+C+C+S+S | MOHGA | 1st | I |
Reg. | ||
| Alcalá et al. | 2007 | Mam. | Ling. | 2 | A+C | SPEA2ACC | 2nd | I |
Reg. | ||
| González et al. | 2007 | TSK | Scat. | 2 | A+C | Non. | 2nd | I |
Reg. | ||
| Gómez-Skarmeta et al. | 2007 | TSK | Scat. | 4 | A+C+C+S | MONEA | 2nd | N | Reg. | ||
| Pulkkinen et al. | 2008 | Mam. | Ling. | 3 | A+C+C | NSGA-II | 2nd | G | Clas. | ||
| Pulkkinen et al. | 2008 | Mam. | Ling. | 3 | A+A+S | NSGA-II | 2nd | G | Clas. | ||
| Guenounou et al. | 2009 | Mam. | Ling.* | 2 | A+C | NSGA-II | 2nd | G | Reg. | ||
| Gacto et al. | 2009 | Mam. | Ling. | 2 | A+C | VARIOUS | 2nd | G | Reg. | ||
| Botta et al. | 2009 | Mam. | Ling. | 2 | A+S | NSGA-II | 2nd | G | Reg. | ||
| Gacto et al. | 2010 | Mam. | Ling. | 3 | A+C+S | SPEA2-SI | 2nd | I |
Reg. | ||
| Marquez et al. | 2009 | Mam. | Ling. | 2 | A+C | VARIOUS | 2nd | I  |
Reg. | ||
| Marquez et al. | 2010 | Mam. | Ling. | 3 | A+C+S | Non. | 2nd | I |
Reg. | ||
| Ishibuchi et al. | 1997, 1998 | Mam. | Ling. | 2 | A+C | Non. | 1st | N | Clas. | ||
| Ishibuchi et al. | 2001 | Mam. | Ling. | 3 | A+C+C | GBML | 1st | N | Clas. | ||
| Ishibuchi et al. | 2004 | Mam. | Ling. | 3 | A+C+C | MOGLS | 1st | N | Clas. | ||
| Ishibuchi et al. | 2006 | Mam. | Ling. | 2 | A+C | NSGA-II | 2nd | G | Clas. | ||
| Ishibuchi et al. | 2007 | Mam. | Ling. | 3 | A+C+C | GBML | 2nd | I |
Clas. | ||
| Alcalá et al. | 2011 | Mam. | Ling. | 3 | A+C+C | NSGA-II | 2nd | G | Clas. | ||
| Setzkorn et al. | 2005 | Mam. | Ling. | 3 | A+C+C | Non. | 2nd | I |
Clas. | ||
| Cococcioni et al. | 2007 | Mam. | Ling. | 2 | A+C | (2+2)M-PAES | 2nd | I |
Reg. | ||
| Xing et al. | 2007 | TSK | Ling. | 2 | A+C | PMOCCA | 2nd | N | Reg.,Ts. | ||
| Ducange et al. | 2010 | Mam. | Ling. | 3 | A+A+C | NSGA-II | 2nd | G | Imb.Clas. | ||
| Cordón et al. | 2003 | Mam. | Ling. | 2 | A+C | Non. | 1st | N | Clas. | ||
| Cococcioni et al. | 2008 | TSK | Scat. | 2 | A+C | (2+2)M-PAES | 2nd | I |
Reg. | ||
| Alcalá et al. | 2009 | Mam. | Ling. | 2 | A+C | (2+2)M-PAES | 2nd | I |
Reg. | ||
| Antonelli et al. | 2009 | Mam. | Ling. | 2 | A+C | (2+2)M-PAES | 2nd | I |
Reg. | ||
| Antonelli et al. | 2009 | Mam. | Ling. | 2 | A+C | (2+2)M-PAES | 2nd | I |
Reg. | ||
| Casillas et al. | 2009 | DNF-RULES | Ling. | 2 | A+C | Non. | 2nd | I |
Reg. | ||
| Pulkkinen et al. | 2010 | Mam. | Ling. | 2 | A+C | Non. | 2nd | I |
Reg. | ||
| Alonso et al. | 2010 | Mam. | Ling. | 3 | A+C+S | NSGA-II | 2nd | G | Clas. | ||
| Cannone et al. | 2011 | Mam. | Ling. | 3 | A+C+S | NSGA-II | 2nd | G | Clas. | ||
| Cannone et al. | 2011 | Mam. | Ling. | 2 | A+S and A+S | NSGA-II | 2nd | G | Clas. | ||
| Cococcioni et al. | 2011 | TSK | Scat. | 2 | A+C | (2+2)M-PAES | 2nd | I |
Reg. | ||
| Antonelli et al. | 2011 | Mam. | Ling. | 3 | A+C+S | (2+2)M-PAES | 2nd | I |
Reg. | ||
| Antonelli et al. | 2011 | Mam. | Ling. | 2 | A+(C+S) | (2+2)M-PAES | 2nd | I |
Reg. | ||
| Alcalá et al. | 2011 | Mam. | Ling. | 2 | A+C | Non | 2nd | I |
Reg. | ||
Mam. = Mamdani, TSK = Takagi-Sugeno-Kang, Ling. = Linguistic, Scat. = Scatter, * = In the antecedent;
A = Accuracy, C = Complexity, S = Semantic aspects;
Non. = No name, N = Novel algorithm, I = Improved version, G = General use;
Clas. = Classification, Reg. = Regression, Ts. = Time Series, Imb. = Imbalanced; NSGA-II based,
NSGA-II based,  PAES based,
PAES based,  MOGA based,
MOGA based,  SPEA2 based.
SPEA2 based.
Application of MOEFSs to multi-objective control problems
The following table presents a summary of MOEFSs for multi-objective control problems.
Table 3. Summary of the proposals on MOEFSs for multi-objective fuzzy control problems.
tabla con formato diferente
| Fuzzy control | FRBS approach | MOEA | ||||||||
| Authors | Year | Rules | Type | #Obj. | Name | Gen. | Type | Application framework | ||
| Ahlawat et al. | 2001 | Mam. | Ling. | 2 | Non. | 1st | I |
Building Vibration | ||
| Ahlawat et al. | 2002, 2004 | Mam. | Ling. | 2 | Non. | 1st | I |
Building Vibration | ||
| Ahlawat et al. | 2002 | Mam. | Ling. | 3 | Non. | 1st | I |
Building Vibration | ||
| Chipperfield et al. | 2002 | Mam. | Ling. | 9 | Non. | 1st | N | Gas turbine engine | ||
| Ahlawat et al. | 2004 | Mam. | Ling. | 2 | Non. | 1st | I |
Building Vibration | ||
| Jurado et al. | 2005 | Mam. | Ling. | 16 | Non. | 1st | I |
Solid oxide fuel cell | ||
| Kim et al. | 2006 | Mam. | Scat. | 2 | NSGA-II | 2nd | G | Base-isolation system | ||
| Kim et al. | 2007 | Mam. | Scat. | 4 | NSGA-II | 2nd | G | Base-isolation system | ||
| Shook et al. | 2008 | Mam. | Ling. | 4 | NSGA-II CE | 2nd | I |
Seismic loads mitigation | ||
| Muñoz et al. | 2008 | Mam. | Ling. | 2 | various | 2nd | G | Fuzzy visual system for robots | ||
| Daum et al. | 2010 | TSK | Scat. | 2 | NSGA-II | 2nd | G | HVAC systems | ||
| Ebner et al. | 2010 |  |
 |
3 | Non. | 2nd | I |
Water treatment | ||
| Gacto et al. | 2012 | Mam. | Ling. | 2 | SPEA2E/E | 2nd | I |
HVAC systems | ||
| Blumel et al. | 2001 | Mam. | Ling. | 4 | NSGA | 1st | N | Missile autopilot | ||
| Chen et al. | 2002 | TSK | Ling.* | 2 | Non. | 1st | N | Incineration process | ||
| Stewart et al. | 2004 | Mam. | Ling. | 3 | Non. | 1st | N | DC motor motion control | ||
| Serra et al. | 2006 | Mam. | Ling. | 3 | Non. | 2nd | N | Nonlinear plants | ||
| Fazendeiro et al. | 2007 | Mam. | Ling. | 2 | Non. | 2nd | I |
Drug dosage for surgeries | ||
Mam. = Mamdani, TSK = Takagi-Sugeno-Kang, Ling. = Linguistic, Scat. = Scatter, * = At antecedents,  Patented FLC, not available information; Patented FLC, not available information;A = Accuracy, C = Complexity, S = Semantic aspects; Non. = No name, N = Novel algorithm, I = Improved version, G = General use;  2-branch tournament GA, 2-branch tournament GA,  MOGA based, MOGA based,  NSGA-II based, NSGA-II based,  SPEA2 based. SPEA2 based. |
||||||||||
Application of MOEFSs Fuzzy Association Rule Mining
The following table presents a summary of the works about MOEFSs for Fuzzy Association Rule Mining
Table 4. Summary of the proposals on MOEFSs for mining fuzzy association rules
tabla con formato diferente
| Fuzzy association rule mining | Objectives | MOEA | ||||||||
| Authors | Year | #Obj. | Description | Name | Gen. | Type | ||||
| Kaya | 2006 | 3 |  Sup.+ Sup.+ Con.+ Con.+ Att. Att. |
Non. | 2nd | N | ||||
| Alhajj et al. | 2008 | 2 |  LI+ LI+ Tim. Tim. |
Non. | 2nd | I |
||||
| Chen et al. | 2008 | 2 |  LI1+ LI1+ Sui. Sui. |
Non. | 1st | I |
||||
| Thilagam et al. | 2008 | 2 |  Sup.+ Sup.+ Con. Con. |
MOGA | 1st | G | ||||
| Casillas et al. | 2009 | 3 |  Err.+ Err.+ DNF-FR+ DNF-FR+ MAM-FR MAM-FR |
Non. | 2nd | I |
||||
| Carmona et al.* | 2010 | 3 |  Sup.+ Sup.+ FCon.+ FCon.+ Unu. Unu. |
NMEEF-SD | 2nd | I |
||||
| *Applied for Subgroup Discovery; Con. = Confidence, Sup. = Support, Tim. = Time, Err. = Error, LI = #Large itemsets, LI1 = #Large 1-itemsets, Att. = #Attributes, Sui. = Suitability; DNF-FR = #DNF-type Fuzzy Rules, MAM-FR = #Equivalent Mamdani-type Fuzzy Rules, Unu. = Unusualness, FConf. = Fuzzy confidence,  = Maximize, = Maximize,  = Minimize, = Minimize,Non. = No name, N = Novel algorithm, I = Improved version, G = General use;  NSGA-II based, NSGA-II based,  PAES based, PAES based,  MOGA based, MOGA based,  SPEA based. SPEA based. |
||||||||||
