Genetic Fuzzy Systems: Taxonomy, Current Research Trends and Prospects
This page contains an introduction to Fuzzy Rule Based Systems, referenced from the paper Website
Genetic Fuzzy Systems: Taxonomy, Current Research Trends and Prospects
Fuzzy Rule Based Systems
The essential part of Fuzzy Rule Based Systems (FRBSs) is a set of IF-THEN linguistic rules, whose antecedents and consequents are composed of fuzzy statements, related by the dual concepts of fuzzy implication and the compositional rule of inference.
An FRBS is composed of a knowledge base (KB), that includes the information in the form of IF-THEN fuzzy rules;
IF a set of conditions are satisfied
THEN a set of consequents can be inferred
and an inference engine module that includes a fuzzification interface, which has the effect of transforming crisp data into fuzzy sets; an inference system, that uses them together with the KB to make inference by means of a reasoning method; and a defuzzification interface, that translates the fuzzy rule action thus obtained to a real action using a defuzzification method.
FRBSs can be broadly categorized into different families. The first includes linguistic models based on collections of IF-THEN rules, whose antecedents are linguistic values, and the system behaviour can be described in natural terms. The consequent is an output action or class to be applied. For example, we can denote them as:
Ri: If Xi1 is Ai1 and ... and Xin is Ain then Y is Bi
or
Ri: If Xi1 is Ai1 and ... and Xin is Ain then Ck with wik
with i = 1 to M, and with Xi1 to Xin and Y being the input and output variables for regression respectively, and Ck the output class associated to the rule for classification, with Ai1 to Ain and Bi being the involved antecedents and consequent labels, respectively, and wik the certain factor associated to the class. They are usually called linguistic FRBSs or Mamdani FRBSs (Mamdani EH. (1974) Applications of fuzzy algorithm for control a simple dynamic plant, Proceedings of the IEEE 121(12):1585-1588).
The second category based on a rule structure that has fuzzy antecedent and functional consequent parts. This can be viewed as the expansion of piece-wise linear partition represented as
Ri: If Xi1 is Ai1 and ... and Xin is Ain then Y = p(Xi1 ,..., Xin).
with p(·) being a polynomial function, usually a linear expression, Y = p0 + p1·Xi1 + ... + pn·Xin. The approach approximates a nonlinear system with a combination of several linear systems. They are called TS-type fuzzy systems (Takagi T, Sugeno M (1985) Fuzzy identification of systems and its application to modelling and control. IEEE Transactions on Systems, Man and Cybernetics 15(1):116-132).
Other kind of fuzzy models are the approximate or scatter partition FRBSs, which differ from the linguistic ones in the direct use of fuzzy variables (Alcalá R, Casillas J, Cordón O, Herrera F. (2001) Building fuzzy graphs: features and taxonomy of learning non-grid-oriented fuzzy rule-based systems, International Journal of Intelligent Fuzzy Systems 11:99-119). Each fuzzy rule thus presents its own semantic, i.e., the variables take different fuzzy sets as values (and not linguistic terms from a global term set). The fuzzy rule structure is then as follow:
Ri: If Xi1 is Âi1 and ... and Xin is Âin then Y is Gi
with Âij to Âin and Gi being fuzzy sets. The major difference with respect to the rule structure considered in linguistic FRBSs is that rules of approximate nature are semantics free whereas descriptive rules operate in the context formulated by means of the linguistic semantics.
In linguistic FRBSs, the KB is comprised by two components, a data base (DB) and a rule base (RB).
- A DB, containing the linguistic term sets considered in the linguistic rules and the membership functions defining the semantics of the linguistic labels.
Each linguistic variable involved in the problem will have associated a fuzzy partition of its domain representing the fuzzy set associated with each of its linguistic terms. Figure 2 shows an example of fuzzy partition with five labels.
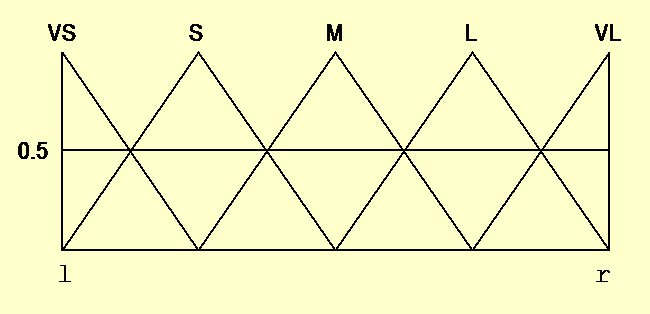
Fig. 2. Example of a fuzzy partition
This can be considered as a discretization approach for continuous domains where we establish a membership degree to the items (labels), we have an overlapping between them, and the inference engine manages the matching between the patterns and the rules providing an output according to the rule consequents with a positive matching. The determination of the fuzzy partitions is crucial in fuzzy modelling (Au W-H, Chan KCC, Wong AKC. (2006) A fuzzy approach to partitioning continuous attributes for classification, IEEE Transactions on Knowledge and Data Engineering 18(5):715-719 doi: 10.1109/TKDE.2006.70), and the granularity of the fuzzy partition plays an important role for the FRBS behaviour (ACordón O, Herrera F, Villar P. (2000) Analysis and guidelines to obtain a good uniform fuzzy partition granularity for fuzzy rule-based systems using simulated annealing, International Journal of Approximate Reasoning 25(3):187-215, doi: 10.1016/S0888-613X(00)00052-9).
If we manage approximate FRBSs, then we do not have a DB due to the fact that rules have associated the fuzzy values.
- An RB, comprised of a collection of linguistic rules that are joined by a rule connective ("also" operator). In other words, multiple rules can fire simultaneously for the same input.
The inference engine of FRBSs acts in a different way depending of the kind of problem (classification or regression) and the kind of fuzzy rules (linguistic ones, TS-ones, ...). It always includes a fuzzfication interface that serves as the input to the fuzzy reasoning process, an inference system that infers from the input to several resulting output (fuzzy set, class, ...) and the defuzzification interface or output interface that converts the fuzzy sets obtained from the inference process into a crisp action that constitutes the global output of the FRBS, in the case of regression problems, or provide the final class associated to the input pattern according to the inference model.
The generic structure of an FRBS is shown in Figure 3.
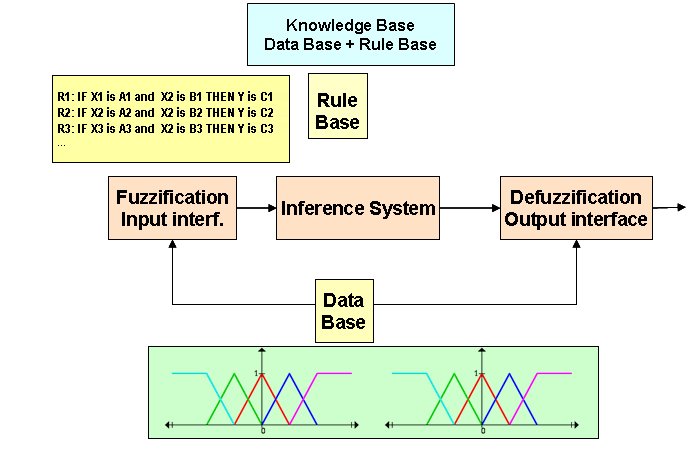
Fig. 3. Structure of an FRBS
For more information about fuzzy systems the following books may be consulted
- Yager RR, Filev DP (1994) Essentials of Fuzzy Modeling and Control, John Wiley & Sons
- Kuncheva L (2000) Fuzzy classifier design, Springer, Berlin
- Cordón O, Herrera F, Hoffmann F, Magdalena L (2001) Genetic fuzzy systems. Evolutionary tuning and learning of fuzzy knowledge bases, World Scientific, Singapore
- Ishibuchi H, Nakashima T, Nii M (2004) Classification and modeling with linguistic information granules: Advanced approaches to linguistic data mining, Springer, Berlin
For different issues associated to the trade-off between interpretability and accuracy of FRBSs, the two following edited books present a collection of contributions in the topic
- Casillas J, Cordón O, Herrera F, Magdalena L (Eds.) (2003) Accuracy improvements in linguistic fuzzy modeling, Springer-Verlag, Berlin
- Casillas J, Cordón O, Herrera F, Magdalena L (Eds.) (2003) Interpretability issues in fuzzy modeling, Springer-Verlag, Berlin
Finally, we must point out that we can find a lot of applications of FRBSs in all areas of engineering, sciences, medicine,… At the present it is very easy to search for these applications using the publisher web search tools focusing the search in journals of different application areas.
