Classification with Imbalanced Datasets
This Website contains SCI2S research material on Classification with Imbalanced Datasets. This research is related to the following SCI2S work published recently: 
V. López, A. Fernandez, S. Garcia, V. Palade and F. Herrera, An Insight into Classification with Imbalanced Data: Empirical Results and Current Trends on Using Data Intrinsic Characteristics. Information Sciences 250 (2013) 113-141 doi: 10.1016/j.ins.2013.07.007 ![]()
The web is organized according to the following summary:
- Introduction to Classification with Imbalanced Datasets
- Imbalanced Datasets in Classification
- Problems related with intrinsic data characteristics
- Addressing Classification with imbalanced data: preprocessing, cost-sensitive learning and ensemble techniques
- Software, Algorithm Implementations and Dataset Repository
- Literature review
Introduction to Classification with Imbalanced Datasets
In many supervised learning applications, there is a significant difference between the prior probabilities of different classes, i.e, between the probabilities with which an example belongs to the different classes of the classification problem. This situation is known as the class imbalance problem (N.V. Chawla, N. Japkowicz, A. Kotcz, Editorial: special issue on learning from imbalanced data sets, SIGKDD Explorations 6 (1) (2004) 1–6. doi: 10.1145/1007730.1007733, H. He, E.A. Garcia, Learning from imbalanced data, IEEE Transactions on Knowledge and Data Engineering 21 (9) (2009) 1263–1284. doi: 10.1109/TKDE.2008.239, Y. Sun, A.K.C. Wong, M.S. Kamel, Classification of imbalanced data: a review, International Journal of Pattern Recognition and Artificial Intelligence 23 (4) (2009) 687–719. doi: 10.1142/S0218001409007326) and it is common in many real problems from telecommunications, web, finance-world, ecology, biology, medicine not only, and which can be considered one of the top problems in data mining today (Q. Yang, X. Wu, 10 challenging problems in data mining research, International Journal of Information Technology and Decision Making 5 (4) (2006) 597–604. doi: 10.1142/S0219622006002258). Furthermore, it is worth to point out that the minority class is usually the one that has the highest interest from a learning point of view and it also implies a great cost when it is not well classified (C. Elkan, The foundations of cost–sensitive learning, in: Proceedings of the 17th IEEE International Joint Conference on Artificial Intelligence (IJCAI’01), 2001, pp. 973–978).
The hitch with imbalanced datasets is that standard classification learning algorithms are often biased towards the majority class (known as the "negative" class) and therefore there is a higher misclassification rate for the minority class instances (called the "positive" examples). Therefore, throughout the last years, many solutions have been proposed to deal with this problem, both for standard learning algorithms and for ensemble techniques (M. Galar, A. Fernández, E. Barrenechea, H. Bustince, F. Herrera, A review on ensembles for class imbalance problem: bagging, boosting and hybrid based approaches, IEEE Transactions on Systems, Man, and Cybernetics – part C: Applications and Reviews 42 (4) (2012) 463–484. doi: 10.1109/TSMCC.2011.2161285). They can be categorized into three major groups:
- Data sampling: In which the training instances are modified in such a way to produce a more or less balanced class distribution that allow classifiers to perform in a similar manner to standard classification (G.E.A.P.A. Batista, R.C. Prati, M.C. Monard, A study of the behaviour of several methods for balancing machine learning training data, SIGKDD Explorations 6 (1) (2004) 20–29. doi: 10.1145/1007730.1007735, N.V. Chawla, K.W. Bowyer, L.O. Hall, W.P. Kegelmeyer, SMOTE: synthetic minority over-sampling technique, Journal of Artificial Intelligent Research 16 (2002) 321–357. doi: 10.1613/jair.953).
- Algorithmic modification: This procedure is oriented towards the adaptation of base learning methods to be more attuned to class imbalance issues (B. Zadrozny, C. Elkan, Learning and making decisions when costs and probabilities are both unknown, in: Proceedings of the 7th International Conference on Knowledge Discovery and Data Mining (KDD’01), 2001, pp. 204–213.).
- Cost-sensitive learning: This type of solutions incorporate approaches at the data level, at the algorithmic level, or at both levels combined, considering higher costs for the misclassification of examples of the positive class with respect to the negative class, and therefore, trying to minimize higher cost errors (P. Domingos, Metacost: a general method for making classifiers cost–sensitive, in: Proceedings of the 5th International Conference on Knowledge Discovery and Data Mining (KDD’99), 1999, pp. 155–164., B. Zadrozny, J. Langford, N. Abe, Cost–sensitive learning by cost–proportionate example weighting, in: Proceedings of the 3rd IEEE International Conference on Data Mining (ICDM’03), 2003, pp. 435–442.).
Most of the studies on the behavior of several standard classifiers in imbalance domains have shown that significant loss of performance is mainly due to the skewed class distribution, given by the imbalance ratio (IR), defined as the ratio of the number of instances in the majority class to the number of examples in the minority class (V. García, J.S. Sánchez, R.A. Mollineda, On the effectiveness of preprocessing methods when dealing with different levels of class imbalance, Knowledge Based Systems 25 (1) (2012) 13–21. doi: 10.1016/j.knosys.2011.06.013, A. Orriols-Puig, E. Bernadó-Mansilla, Evolutionary rule-based systems for imbalanced datasets, Soft Computing 13 (3) (2009) 213–225. doi: 10.1007/s00500-008-0319-7). However, there are several investigations which also suggest that there are other factors that contribute to such performance degradation (N. Japkowicz, S. Stephen, The class imbalance problem: a systematic study, Intelligent Data Analysis Journal 6 (5) (2002) 429–450.). Therefore, as a second goal, we present a discussion about six significant problems related to data intrinsic characteristics and that must be taken into account in order to provide better solutions for correctly identifying both classes of the problem:
- The identification of areas with small disjuncts (G.M. Weiss, Mining with rare cases, in: O. Maimon, L. Rokach (Eds.), The Data Mining and Knowledge Discovery Handbook, Springer, 2005, pp. 765–776., G.M. Weiss, The impact of small disjuncts on classifier learning, in: R. Stahlbock, S.F. Crone, S. Lessmann (Eds.), Data Mining: Annals of Information Systems, vol. 8, Springer, 2010, pp. 193–226.).
- The lack of density and information in the training data (M. Wasikowski, X.-W. Chen, Combating the small sample class imbalance problem using feature selection, IEEE Transactions on Knowledge and Data Engineering 22 (10) (2010) 1388–1400. doi: 10.1109/TKDE.2009.187).
- The problem of overlapping between the classes (M. Denil, T. Trappenberg, Overlap versus imbalance, in: Proceedings of the 23rd Canadian Conference on Advances in Artificial Intelligence (CCAI’10), Lecture Notes on Artificial Intelligence, vol. 6085, 2010, pp. 220–231., V. García, R.A. Mollineda, J.S. Sánchez, On the k-NN performance in a challenging scenario of imbalance and overlapping, Pattern Analysis Applications 11 (3–4) (2008) 269–280. doi: 10.1007/s10044-007-0087-5).
- The impact of noisy data in imbalanced domains (C.E. Brodley, M.A. Friedl, Identifying mislabeled training data, Journal of Artificial Intelligence Research 11 (1999) 131–167. doi: 10.1613/jair.606, C. Seiffert, T.M. Khoshgoftaar, J. Van Hulse, A. Folleco, An empirical study of the classification performance of learners on imbalanced and noisy software quality data, Information Sciences (2013), In press. doi: 10.1016/j.ins.2010.12.016).
- The significance of the borderline instances to carry out a good discrimination between the positive and negative classes, and its relationship with noisy examples (D.J. Drown, T.M. Khoshgoftaar, N. Seliya, Evolutionary sampling and software quality modeling of high-assurance systems, IEEE Transactions on Systems, Man, and Cybernetics, Part A 39 (5) (2009) 1097–1107. doi: 10.1109/TSMCA.2009.2020804, K. Napierala, J. Stefanowski, S. Wilk, Learning from imbalanced data in presence of noisy and borderline examples, in: Proceedings of the 7th International Conference on Rough Sets and Current Trends in Computing (RSCTC’10), Lecture Notes on Artificial Intelligence, vol. 6086, 2010, pp. 158–167.).
- The possible differences in the data distribution for the training and test data, also known as the dataset shift (J.G. Moreno-Torres, X. Llorà, D.E. Goldberg, R. Bhargava, Repairing fractures between data using genetic programming-based feature extraction: a case study in cancer diagnosis, Information Sciences 222 (2013) 805–823. doi: 10.1016/j.ins.2010.09.018, H. Shimodaira, Improving predictive inference under covariate shift by weighting the log-likelihood function, Journal of Statistical Planning and Inference 90 (2) (2000) 227–244. doi: 10.1016/S0378-3758(00)00115-4).
This thorough study of the problem can guide us about the source where the difficulties for imbalanced classification emerge, focusing on the analysis of significant data intrinsic characteristics. Specifically, for each established scenario we show an experimental example on how it affects the behavior of the learning algorithms, in order to stress its significance.
We must point out that some of these topics have recent studies associated, examining their main contributions and recommendations. However, we emphasize that they still need to be addressed in more detail in order to have models of high quality in this classification scenario and, therefore, we have stressed them as future trends of research for imbalanced learning. Overcoming these problems can be the key for developing new approaches that improve the correct identification of both the minority and majority classes.
Imbalanced Datasets in Classification
The problem of imbalanced datasets
In the classification problem field, the scenario of imbalanced datasets appears frequently. The main property of this type of classification problem is that the examples of one class significantly outnumber the examples of the other one (H. He, E.A. Garcia, Learning from imbalanced data, IEEE Transactions on Knowledge and Data Engineering 21 (9) (2009) 1263–1284. doi: 10.1109/TKDE.2008.239, Y. Sun, A.K.C. Wong, M.S. Kamel, Classification of imbalanced data: a review, International Journal of Pattern Recognition and Artificial Intelligence 23 (4) (2009) 687–719. doi: 10.1142/S0218001409007326). The minority class usually represents the most important concept to be learned, and it is difficult to identify it since it might be associated with exceptional and significant cases (G.M. Weiss, Mining with rarity: a unifying framework, SIGKDD Explorations 6 (1) (2004) 7–19. doi: 10.1145/1007730.1007734), or because the data acquisition of these examples is costly (G.M. Weiss, Y. Tian, Maximizing classifier utility when there are data acquisition and modeling costs, Data Mining and Knowledge Discovery 17 (2) (2008) 253–282. doi: 10.1007/s10618-007-0082-x). In most cases, the imbalanced class problem is associated to binary classification, but the multi-class problem often occurs and, since there can be several minority classes, it is more difficult to solve (A. Fernández, V. López, M. Galar, M.J. del Jesus, F. Herrera, Analysing the classification of imbalanced data-sets with multiple classes: binarization techniques and ad-hoc approaches, Knowledge-Based Systems 42 (2013) 97–110. doi: 10.1016/j.knosys.2013.01.018, M. Lin, K. Tang, X. Yao, Dynamic sampling approach to training neural networks for multiclass imbalance classification, IEEE Transactions on Neural Networks and Learning Systems 24 (4) (2013) 647–660. doi: 10.1109/TNNLS.2012.2228231).
Since most of the standard learning algorithms consider a balanced training set, this may generate suboptimal classification models, i.e. a good coverage of the majority examples, whereas the minority ones are misclassified frequently. Therefore, those algorithms, which obtain a good behavior in the framework of standard classification, do not necessarily achieve the best performance for imbalanced datasets (A. Fernandez, S. García, J. Luengo, E. Bernadó-Mansilla, F. Herrera, Genetics-based machine learning for rule induction: state of the art, taxonomy and comparative study, IEEE Transactions on Evolutionary Computation 14 (6) (2010) 913–941. doi: 10.1109/TEVC.2009.2039140). There are several reasons behind this behavior:
- The use of global performance measures for guiding the learning process, such as the standard accuracy rate, may provide an advantage to the majority class.
- Classification rules that predict the positive class are often highly specialized and thus their coverage is very low, hence they are discarded in favor of more general rules, i.e. those that predict the negative class.
- Very small clusters of minority class examples can be identified as noise, and therefore they could be wrongly discarded by the classifier. On the contrary, few real noisy examples can degrade the identification of the minority class, since it has fewer examples to train with.
In recent years, the imbalanced learning problem has received much attention from the machine learning community. Regarding real world domains, the importance of the imbalance learning problem is growing, since it is a recurring issue in many applications. As some examples, we could mention very high resolution airbourne imagery (X. Chen, T. Fang, H. Huo, D. Li, Graph-based feature selection for object-oriented classification in VHR airborne imagery, IEEE Transactions on Geoscience and Remote Sensing 49 (1) (2011) 353–365. doi: 10.1109/TGRS.2010.2054832), forecasting of ozone levels (C.-H. Tsai, L.-C. Chang, H.-C. Chiang, Forecasting of ozone episode days by cost-sensitive neural network methods, Science of the Total Environment 407 (6) (2009) 2124–2135. doi: 10.1016/j.scitotenv.2008.12.007), face recognition (N. Kwak, Feature extraction for classification problems and its application to face recognition, Pattern Recognition 41 (5) (2008) 1718–1734. doi: 10.1016/j.patcog.2007.10.015), and especially medical diagnosis (R. Batuwita, V. Palade, microPred: effective classification of pre-miRNAs for human miRNA gene prediction, Bioinformatics 25 (8) (2009) 989–995. doi: 10.1093/bioinformatics/btp107, H.-Y. Lo, C.-M. Chang, T.-H. Chiang, C.-Y. Hsiao, A. Huang, T.-T. Kuo, W.-C. Lai, M.-H. Yang, J.-J. Yeh, C.-C. Yen, S.-D. Lin, Learning to improve area-under-FROC for imbalanced medical data classification using an ensemble method, SIGKDD Explorations 10 (2) (2008) 43–46. doi: 10.1145/1540276.1540290, M.A. Mazurowski, P.A. Habas, J.M. Zurada, J.Y. Lo, J.A. Baker, G.D. Tourassi, Training neural network classifiers for medical decision making: the effects of imbalanced datasets on classification performance, Neural Networks 21 (2–3) (2008). doi: 10.1016/j.neunet.2007.12.031, L. Mena, J.A. González, Symbolic one-class learning from imbalanced datasets: application in medical diagnosis, International Journal on Artificial Intelligence Tools 18 (2) (2009) 273–309. doi: 10.1142/S0218213009000135, Z. Wang, V. Palade, Building interpretable fuzzy models for high dimensional data analysis in cancer diagnosis, BMC Genomics 12 ((S2):S5) (2011). doi: 10.1186/1471-2164-12-S2-S5). It is important to remember that the minority class usually represents the concept of interest and it is the most difficult to obtain from real data, for example patients with illnesses in a medical diagnosis problem; whereas the other class represents the counterpart of that concept (healthy patients).
Evaluation in imbalanced domains
The evaluation criteria is a key factor in assessing the classification performance and guiding the classifier modeling. In a two-class problem, the confusion matrix (shown in Table 1) records the results of correctly and incorrectly recognized examples of each class.
| Positive prediction | Negative prediction | |
| Positive class | True Positive (TP) | False Negative (FN) |
| Negative class | False Positive (FP) | True Negative (TN) |
Traditionally, the accuracy rate (Equation 1) has been the most commonly used empirical measure. However, in the framework of imbalanced datasets, accuracy is no longer a proper measure, since it does not distinguish between the number of correctly classified examples of different classes. Hence, it may lead to erroneous conclusions, i.e., a classifier achieving an accuracy of 90% in a dataset with an IR value of 9 is not accurate if it classifies all examples as negatives.
$$Acc=\frac{TP+TN}{TP+FN+FP+TN} \ (Equation \ 1)$$
In imbalanced domains, the evaluation of the classifiers' performance must be carried out using specific metrics in order to take into account the class distribution. Concretely, we can obtain four metrics from Table 1 to measure the classification performance of both, positive and negative, classes independently:
- True positive rate: $TP_{rate}=\frac{TP}{TP+FN}$ is the percentage of positive instances correctly classified.
- True negative rate: $TN_{rate}=\frac{TN}{FP+TN}$ is the percentage of negative instances correctly classified.
- False positive rate: $FP_{rate}=\frac{FP}{FP+TN}$ is the percentage of negative instances misclassified.
- False negative rate: $FN_{rate}=\frac{FN}{TP+FN}$ is the percentage of positive instances misclassified.
Since in this classification scenario we intend to achieve good quality results for both classes, there is a necessity of combining the individual measures of both the positive and negative classes, as none of these measures alone is adequate by itself.
A well-known approach to unify these measures and to produce an evaluation criteria is to use the Receiver Operating Characteristic (ROC) graphic (A.P. Bradley, The use of the area under the roc curve in the evaluation of machine learning algorithms, Pattern Recognition 30 (7) (1997) 1145–1159. doi: 10.1016/S0031-3203(96)00142-2). This graphic allows the visualization of the trade-off between the benefits (TPrate) and costs (FPrate), as it evidences that any classifier cannot increase the number of true positives without also increasing the false positives. The Area Under the ROC Curve (AUC) (J. Huang, C.X. Ling, Using AUC and accuracy in evaluating learning algorithms, IEEE Transactions on Knowledge and Data Engineering 17 (3) (2005) 299–310. doi: 10.1109/TKDE.2005.50) corresponds to the probability of correctly identifying which one of the two stimuli is noise and which one is signal plus noise. The AUC provides a single measure of a classifier's performance for evaluating which model is better on average. Figure 1 shows how to build the ROC space plotting on a two-dimensional chart the TPrate (Y-axis) against the FPrate (X-axis). Points in (0,0) and (1,1) are trivial classifiers where the predicted class is always the negative and positive one, respectively. On the contrary, (0,1) point represents the perfect classifier. The AUC measure is computed just by obtaining the area of the graphic:
$$AUC=\frac{1+TP_{rate}-FP_{rate}}{2} \ (Equation \ 2)$$
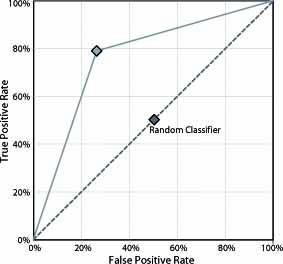
Figure 1. Example of a ROC plot. Two classifiers' curves are depicted: the dashed line represents a random classifier, whereas the solid line is a classifier which is better than the random classifier
In R.C. Prati, G.E.A.P.A. Batista, M.C. Monard, A survey on graphical methods for classification predictive performance evaluation, IEEE Transactions on Knowledge and Data Engineering 23 (11) (2011) 1601–1618. doi: 10.1109/TKDE.2011.59, the significance of these graphical methods for the classification predictive performance evaluation is stressed. According to the authors, the main advantage of this type of methods resides in their ability to depict the trade-offs between evaluation aspects in a multidimensional space rather than reducing these aspects to an arbitrarily chosen (and often biased) single scalar measure. In particular, they present a review of several representation mechanisms emphasizing the best scenario for their use; for example, in imbalanced domains, when we are interested in the positive class, it is recommended the use of precision-recall graphs (J. Davis, M. Goadrich, The relationship between precisionrecall and ROC curves, in: Proceedings of the 23th International Conference on Machine Learning (ICML’06), ACM, 2006, pp. 233–240.). Furthermore, the expected cost or profit of each model might be analyzed using cost curves (C. Drummond, R.C. Holte, Cost curves: an improved method for visualizing classifier performance, Machine Learning 65 (1) (2006) 95–130. doi: 10.1007/s10994-006-8199-5), lift and ROI graphs (H.-Y. Lo, C.-M. Chang, T.-H. Chiang, C.-Y. Hsiao, A. Huang, T.-T. Kuo, W.-C. Lai, M.-H. Yang, J.-J. Yeh, C.-C. Yen, S.-D. Lin, Learning to improve area-under-FROC for imbalanced medical data classification using an ensemble method, SIGKDD Explorations 10 (2) (2008) 43–46. doi: 10.1145/1540276.1540290).
Other metric of interest to be stressed in this area is the geometric mean of the true rates (R. Barandela, J.S. Sánchez, V. García, E. Rangel, Strategies for learning in class imbalance problems, Pattern Recognition 36 (3) (2003) 849–851. doi: 10.1016/S0031-3203(02)00257-1), which can be defined as:
$$GM=\sqrt{\frac{TP}{TP+FN} · \frac{TN}{FP+TN}} \ (eQUATION 3)$$
This metric attempts to maximize the accuracy on each of the two classes with a good balance, being a performance metric that correlates both objectives. However, due to this symmetric nature of the distribution of the geometric mean over TPrate (sensitivity) and the TNrate (specificity), it is hard to contrast different models according to their precision on each class.
Another significant performance metric that is commonly used is the F-measure (R. Baeza-Yates, B. Ribeiro-Neto, Modern Information Retrieval, Addison Wesley, 1999):
$$F_m=\frac{(1+ \beta ^2)(PPV·TP_{rate})}{\beta ^2 PPV+TP_{rate}} \ (Equation \ 4)$$
$$PPV=\frac{TP}{TP+FP}$$
A popular choice for β is 1, where equal importance is assigned for both TPrate and the positive predictive value (PPV). This measure would be more sensitive to the changes in the PPV than to the changes in TPrate, which can lead to the selection of sub-optimal models.
According to the previous comments, some authors try to propose several measures for imbalanced domains in order to be able to obtain as much information as possible about the contribution of each class to the final performance and to take into account the IR of the dataset as an indication of its difficulty. For example, in R. Batuwita, V. Palade, AGm: a new performance measure for class imbalance learning. application to bioinformatics problems, in: Proceedings of the 8th International Conference on Machine Learning and Applications (ICMLA 2009), 2009, pp. 545–550. and R. Batuwita, V. Palade, Adjusted geometric-mean: a novel performance measure for imbalanced bioinformatics datasets learning, Journal of Bioinformatics and Computational Biology 10 (4) (2012). doi: 10.1142/S0219720012500035, the Adjusted G-mean is proposed. This measure is designed towards obtaining the highest sensitivity (TPrate) without decreasing too much the specificity (TNrate). This fact is measured with respect to the original model, i.e. the original classifier without addressing the class imbalance problem. Equation 5 shows its definition:
$$AGM=\frac{GM+TN_{rate}·(FP+TN)}{1+FP+TN}; \ If TP_{rate} > 0$$
$$AGM = 0: \ If TP_{rate}=0 \ (Equation \ 5)$$
Additionally, in V. García, R.A. Mollineda, J.S. Sánchez, A new performance evaluation method for two-class imbalanced problems, in: Proceedings of the Structural and Syntactic Pattern Recognition (SSPR’08) and Statistical Techniques in Pattern Recognition (SPR’08), Lecture Notes on Computer Science, vol. 5342, 2008, pp. 917–925. the authors presented a simple performance metric, called Dominance, which is aimed to point out the dominance or prevalence relationship between the positive class and the negative class, in the range [-1,+1] (Equation 6). Furthermore, it can be used as a visual tool to analyze the behavior of a classifier on a 2-D space from the joint perspective of global precision (Y-axis) and dominance (X-axis).
$$Dom=TP_{rate}-TN_{rate} \ (Equation \ 6)$$
The same authors, using the previous concept of dominance, define a new metric called Index of Balanced Accuracy (IBA) (V. García, R.A. Mollineda, J.S. Sánchez, Theoretical analysis of a performance measure for imbalanced data, in: 20th International Conference on Pattern Recognition (ICPR’10), 2010, pp. 617–620, V. García, R.A. Mollineda, J.S. Sánchez, Classifier performance assessment in two-class imbalanced problems, Internal Communication (2012)). IBA weights a performance measure, that aims to make it more sensitive for imbalanced domains. The weighting factor favors those results with moderately better classification rates on the minority class. IBA is formulated as follows:
$$IBA_{\alpha}(M)=(1+\alpha · Dom)M \ (Equation \ 7)$$
where (1 + α · Dom) is the weighting factor and M represents a performance metric. The objective is to moderately favor the classification models with higher prediction rate on the minority class (without underestimating the relevance of the majority class) by means of a weighted function of any plain performance evaluation measure.
A comparison regarding these evaluation proposals for imbalanced datasets is out of the scope of this web. For this reason, we refer any interested reader to find a deep experimental study in V. García, R.A. Mollineda, J.S. Sánchez, Classifier performance assessment in two-class imbalanced problems, Internal Communication (2012) and T. Raeder, G. Forman, N.V. Chawla, Learning from imbalanced data: evaluation matters, in: D.E. Holmes, L.C. Jain (Eds.), Data Mining: Found. and Intell. Paradigms, vol. ISRL 23, Springer-Verlag, 2012, pp. 315–331.
Problems related to intrinsic data characteristics
As it was stated in the introduction of this web, skewed class distributions do not hinder the learning task by itself (H. He, E.A. Garcia, Learning from imbalanced data, IEEE Transactions on Knowledge and Data Engineering 21 (9) (2009) 1263–1284. doi: 10.1109/TKDE.2008.239, Y. Sun, A.K.C. Wong, M.S. Kamel, Classification of imbalanced data: a review, International Journal of Pattern Recognition and Artificial Intelligence 23 (4) (2009) 687–719. doi: 10.1142/S0218001409007326), but usually a series of difficulties related with this problem turn up. This issue is depicted in Figure 2, in which we show the performance of the C4.5 decision tree with the SMOTEBagging ensemble (S. Wang, X. Yao, Diversity analysis on imbalanced data sets by using ensemble models, in: Proceedings of the 2009 IEEE Symposium on Computational Intelligence and Data Mining (CIDM'09), 2009, pp. 324–331) with 66 datasets with an IR ranging from 1.82 to 128.87, ordered according to the IR, in order to search for some regions of interesting good or bad behavior. As we can observe, there is no pattern of behavior for any range of IR, and the results can be poor both for low and high imbalanced data.
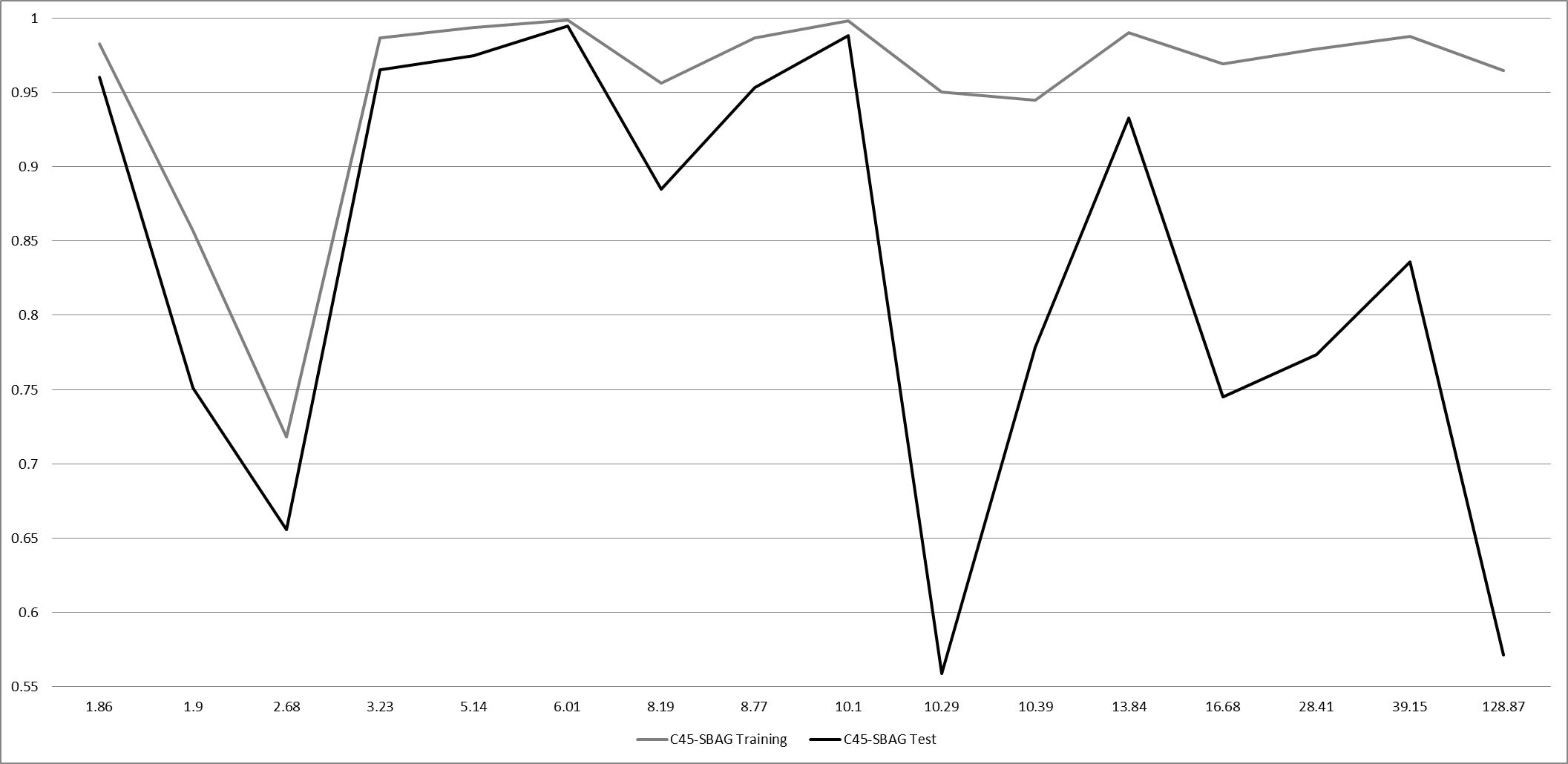
Figure 2. Performance in training and testing for the C4.5 decision tree with the SMOTEBagging ensemble as a function of IR
Related to this issue, in this section we aim to make a discussion on the nature of the problem itself, emphasizing several data intrinsic characteristics that do have a strong influence on imbalanced classification, in order to be able to address this problem in a more feasible way.
With this objective in mind, we focus our analysis on using the C4.5 classifier, in order to develop a basic but descriptive study by showing a series of patterns of behavior, following a kind of "educational scheme". With respect to the previous section, which was carried out in an empirical way, this part of the study is devoted to enumerating the scenarios that can be found when dealing with classification with imbalanced data, emphasizing their main issues that will allow us to design a better algorithm that can be adapted to different niches of the problem.
We acknowledge that some of the data intrinsic characteristics described along this section share some features and it is usual that, for a given dataset, several "sub-problems" can be found simultaneously. Nevertheless, we consider a simplified view of all these scenarios to serve as a global introduction to the topic.
Small disjuncts
The presence of the imbalanced classes is closely related to the problem of small disjuncts. This situation occurs when the concepts are represented within small clusters, which arise as a direct result of underrepresented subconcepts (A. Orriols-Puig, E. Bernadó-Mansilla, D.E. Goldberg, K. Sastry, P.L. Lanzi, Facetwise analysis of XCS for problems with class imbalances, IEEE Transactions on Evolutionary Computation 13 (2009) 260–283. doi: 10.1109/TEVC.2009.2019829, G.M. Weiss, F.J. Provost, Learning when training data are costly: the effect of class distribution on tree induction, Journal of Artificial Intelligence Research 19 (2003) 315–354. doi: 10.1613/jair.1199). Although those small disjuncts are implicit in most of the problems, the existence of this type of areas highly increases the complexity of the problem in the case of class imbalance, because it becomes hard to know whether these examples represent an actual subconcept or are merely attributed to noise (T. Jo, N. Japkowicz, Class imbalances versus small disjuncts, ACM SIGKDD Explorations Newsletter 6 (1) (2004) 40–49 doi: 10.1145/1007730.1007737). This situation is represented in Figure 3, where we show an artificially generated dataset with small disjuncts for the minority class and the "Subclus" problem created in K. Napierala, J. Stefanowski, S. Wilk, Learning from imbalanced data in presence of noisy and borderline examples, in: Proceedings of the 7th International Conference on Rough Sets and Current Trends in Computing (RSCTC'10), Lecture Notes on Artificial Intelligence, vol. 6086, 2010, pp. 158–167, where we can find small disjuncts for both classes: the negative samples are underrepresented with respect to the positive samples in the central region of positive rectangular areas, while the positive samples only cover a small part of the whole dataset and are placed inside the negative class. We must point out that, in all figures of this web, positive instances are represented with dark stars whereas negative instances are depicted with light circles.
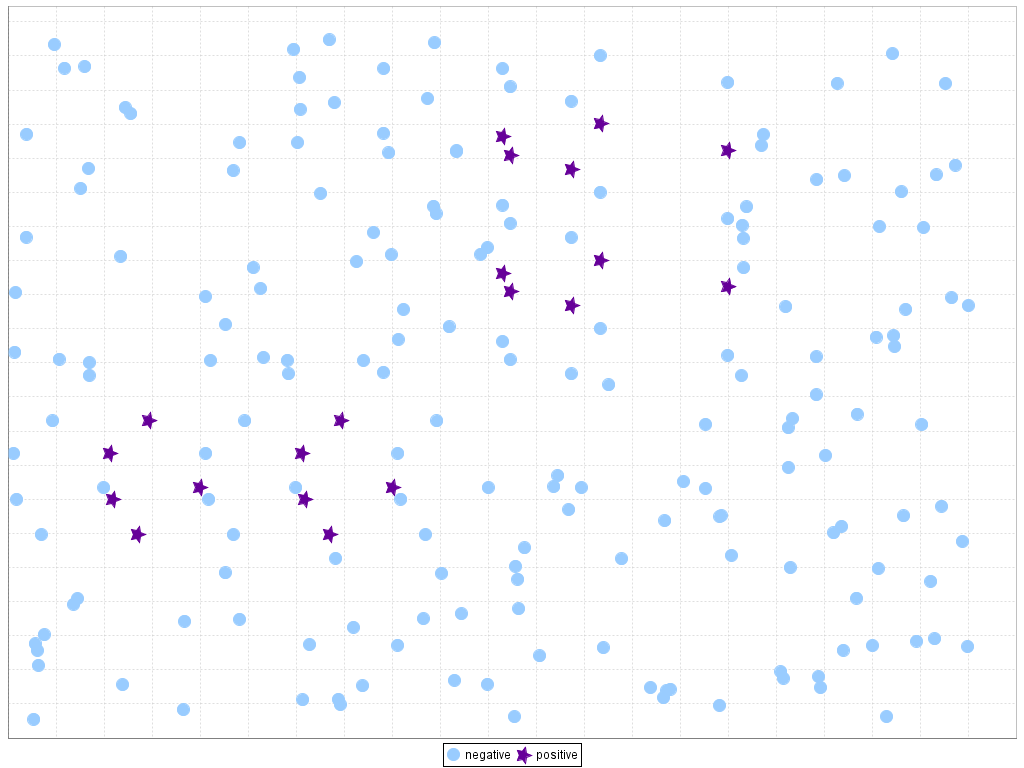
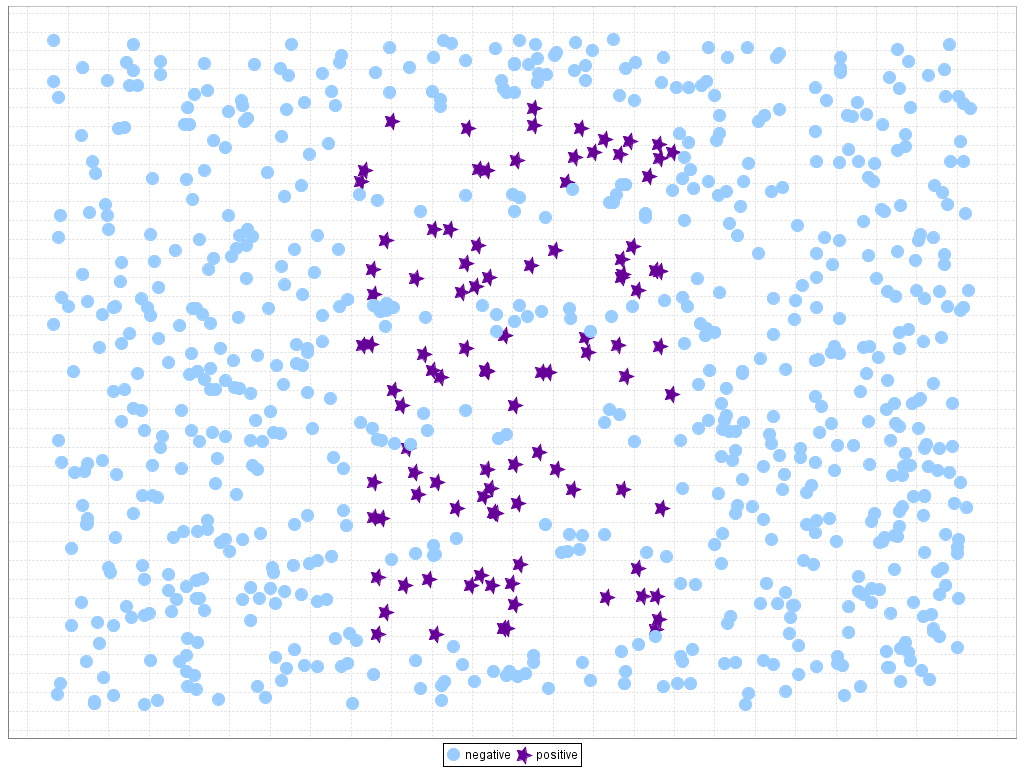
Figure 3. Example of small disjuncts on imbalanced data
The problem of small disjuncts becomes accentuated for those classification algorithms which are based on a divide-and-conquer approach (G.M. Weiss, Mining with rarity: a unifying framework, SIGKDD Explorations 6 (1) (2004) 7–19. doi: 10.1145/1007730.1007734). This methodology consists in subdividing the original problem into smaller ones, such as the procedure used in decision trees, and can lead to data fragmentation (J.H. Friedman, R. Kohavi, Y. Yun, Lazy decision trees, in: Proceedings of the AAAI/IAAI, vol. 1, 1996, pp. 717–724), that is, to obtain several partitions of data with a few representation of instances. If the IR of the data is high, this handicap is obviously more severe.
Several studies by Weiss (G.M. Weiss, Mining with rare cases, in: O. Maimon, L. Rokach (Eds.), The Data Mining and Knowledge Discovery Handbook, Springer, 2005, pp. 765–776, G.M. Weiss, The impact of small disjuncts on classifier learning, in: R. Stahlbock, S.F. Crone, S. Lessmann (Eds.), Data Mining: Annals of Information Systems, vol. 8, Springer, 2010, pp. 193–226) analyze this factor in depth and enumerate several techniques for handling the problem of small disjuncts:
- Obtain additional training data. The lack of data can induce the apparition of small disjuncts, especially in the minority class, and these areas may be better covered just by employing an informed sampling scheme (N. Japkowicz, Concept-learning in the presence of between-class and within-class imbalances, in: E. Stroulia, S. Matwin (Eds.), Proceedings of the 14th Canadian Conference on Advances in Artificial Intelligence (CCAI'08), Lecture Notes in Computer Science, vol. 2056, Springer, 2001, pp. 67–77).
- Use a more appropriate inductive bias. If we aim to be able to properly detect the areas of small disjuncts, some sophisticated mechanisms must be employed for avoiding the preference for the large areas of the problem. For example, R.C. Holte, L. Acker, B.W. Porter, Concept learning and the problem of small disjuncts, in: Proceedings of the International Joint Conferences on Artificial Intelligence, IJCAI'89, 1989, pp. 813–818 modified CN2 so that its maximum generality bias is used only for large disjuncts, and a maximum specificity bias was then used for small disjuncts. However, this approach also degrades the performance of the small disjuncts, and some authors proposed to refine the search and to use different learners for the examples that fall in the large disjuncts and on the small disjuncts separately (D.R. Carvalho, A.A. Freitas, A hybrid decision tree/genetic algorithm method for data mining, Information Sciences 163 (1–3) (2004) 13–35. doi: 10.1016/j.ins.2003.03.013, K.M. Ting, The problem of small disjuncts: its remedy in decision trees, in: Proceedings of the 10th Canadian Conference on Artificial Intelligence (CCAI'94), 1994, pp. 91–97).
- Using more appropriate metrics. This issue is related to the previous one in the sense that, for the data mining process, it is recommended to use specific measures for imbalanced data, in a way that the minority classes in the small disjuncts are positively weighted when obtaining the classification model (G.M. Weiss, Timeweaver: a genetic algorithm for identifying pre-dictive patterns in sequences of events, in: W. Banzhaf, J. Daida, A.E. Eiben, M.H. Garzon, V. Honavar, M. Jakiela, R.E. Smith (Eds.), Proceedings of the Genetic and Evolutionary Computation Conference GECCO'99, vol. 1, Morgan Kaufmann, Orlando, Florida, USA, 1999, pp. 718–725). For example, the use of precision and recall for the minority and majority classes, respectively, can lead to generate more precise rules for the positive class (P. Ducange, B. Lazzerini, F. Marcelloni, Multi-objective genetic fuzzy classifiers for imbalanced and cost-sensitive datasets, Soft Computing 14 (7) (2010) 713–728. doi: 10.1007/s00500-009-0460-y, M.V. Joshi, V. Kumar, R.C. Agarwal, Evaluating boosting algorithms to classify rare classes: comparison and improvements, in: Proceedings of the 2001 IEEE International Conference on Data Mining (ICDM'01), IEEE Computer Society, Washington, DC, USA, 2001, pp. 257–264).
- Disabling pruning. Pruning tends to eliminate most small disjuncts by a generalization of the obtained rules. Therefore, this methodology is not recommended.
- Employ boosting. Boosting algorithms, such as the AdaBoost algorithm, are iterative algorithms that place different weights on the training distribution each iteration (R.E. Schapire, A brief introduction to boosting, in: Proceedings of the International Joint Conference on Artificial Intelligence (IJCAI'99), 1999, pp. 1401–1406). Following each iteration, boosting increases the weights associated with the incorrectly classified examples and decreases the weights associated with the correctly classified examples. Because instances in the small disjuncts are known to be difficult to predict, it is reasonable to believe that boosting will improve their classification performance. Following this idea, many approaches have been developed by modifying the standard boosting weight-update mechanism in order to improve the performance on the minority class and the small disjuncts (N.V. Chawla, A. Lazarevic, L.O. Hall, K.W. Bowyer, SMOTEBoost: Improving prediction of the minority class in boosting, in: Proceedings of 7th European Conference on Principles and Practice of Knowledge Discovery in Databases (PKDD'03), 2003, pp. 107–119, W. Fan, S.J. Stolfo, J. Zhang, P.K. Chan, Adacost: misclassification cost-sensitive boosting, in: Proceedings of the 16th International Conference on Machine Learning (ICML'96), Morgan Kaufmann Publishers Inc., San Francisco, CA, USA, 1999, pp. 97–105, H. Guo, H.L. Viktor, Learning from imbalanced data sets with boosting and data generation: the DataBoost-IM approach, SIGKDD Explorations Newsletter 6 (2004) 30–39. doi: 10.1145/1007730.1007736, S. Hu, Y. Liang, L. Ma, Y. He, MSMOTE: improving classification performance when training data is imbalanced, in: Proceedings of the 2nd International Workshop on Computer Science and Engineering (WCSE'09), vol. 2, 2009, pp. 13–17, M.V. Joshi, V. Kumar, R.C. Agarwal, Evaluating boosting algorithms to classify rare classes: comparison and improvements, in: Proceedings of the 2001 IEEE International Conference on Data Mining (ICDM'01), IEEE Computer Society, Washington, DC, USA, 2001, pp. 257–264, C. Seiffert, T.M. Khoshgoftaar, J. Van Hulse, A. Napolitano, RUSBoost: a hybrid approach to alleviating class imbalance, IEEE Transactions on System, Man and Cybernetics A 40 (1) (2010) 185–197. doi: 10.1109/TSMCA.2009.2029559, Y. Sun, M.S. Kamel, A.K.C. Wong, Y. Wang, Cost-sensitive boosting for classification of imbalanced data, Pattern Recognition 40 (12) (2007) 3358–3378. doi: 10.1016/j.patcog.2007.04.009, K.M. Ting, A comparative study of cost-sensitive boosting algorithms, in: Proceedings of the 17th International Conference on Machine Learning (ICML'00), Stanford, CA, USA, 2000, pp. 983–990).
Finally, we must emphasize the use of the CBO method (T. Jo, N. Japkowicz, Class imbalances versus small disjuncts, ACM SIGKDD Explorations Newsletter 6 (1) (2004) 40–49. doi: 10.1145/1007730.1007737), which is a resampling strategy that is used to counteract simultaneously the between-class imbalance and the within-class imbalance. Specifically, this approach detects the clusters in the positive and negative classes using the k-means algorithm in a first step. In a second step, it randomly replicates the examples for each cluster (except the largest negative cluster) in order to obtain a balanced distribution between clusters from the same class and between classes. These clusters can be viewed as small disjuncts in the data, and therefore this preprocessing mechanism is aimed to stress the significance of these regions.
In order to show the goodness of this approach, we depict a short analysis on the two previously presented artificial datasets, that is, our artificial problem and the Subclus dataset, studying the behavior of the C4.5 classifier according to both the differences in performance between the original and the preprocessed data and the boundaries obtained in each case. We must point out that the whole dataset is used in both cases.
Table 2 shows the results of C4.5 in each case, where we must emphasize that the application of CBO enables the correct identification of all the examples for both classes. Regarding the visual output of the C4.5 classifier (Figure 4), in the first case we observe that for the original data no instances of the positive class are recognized, and that there is an overgeneralization of the negative instances, whereas the CBO method achieves the correct identification of the four clusters in the data, by replicating an average of 11.5 positive examples and 1.25 negative examples. In the Subclus problem, there is also an overgeneralization for the original training data, but in this case we found that the small disjuncts of the negative class surrounding the positive instances are the ones which are misclassified now. Again, the application of the CBO approach results on a perfect classification for all data, having 7.8 positive instances for each "data point" and 1.12 negative ones.
| Dataset | Original Data | Preprocessed Data with CBO | ||||
| TPrate | TNrate | AUC | TPrate | TNrate | AUC | |
| Artificial dataset | 0.0000 | 1.0000 | 0.5000 | 1.0000 | 1.0000 | 1.0000 |
| Subclus dataset | 1.0000 | 0.9029 | 0.9514 | 1.0000 | 1.0000 | 1.0000 |




Figure 4. Boundaries obtained by C4.5 with the original and preprocessed data using CBO for addressing the problem of small disjuncts. The new instances for CBO are just replicates of the initial examples
Lack of density
One problem that can arise in classification is the small sample size (S.J. Raudys, A.K. Jain, Small sample size effects in statistical pattern recognition: recommendations for practitioners, IEEE Transactions on Pattern Analysis and Machine Intelligence 13 (3) (1991) 252–264. doi: 10.1109/34.75512). This issue is related to the "lack of density" or "lack of information", where induction algorithms do not have enough data to make generalizations about the distribution of samples, a situation that becomes more difficult in the presence of high dimensional and imbalanced data. A visual representation of this problem is depicted in Figure 5, where we show a scatter plot for the training data of the yeast4 problem (attributes mcg vs. gvh) only with a 10% of the original instances and with all the data. We can appreciate that it becomes very hard for the learning algorithm to obtain a model that is able to perform a good generalization when there is not enough data that represents the boundaries of the problem and, what it is also most significant, when the concentration of minority examples is so low that they can be simply treated as noise.
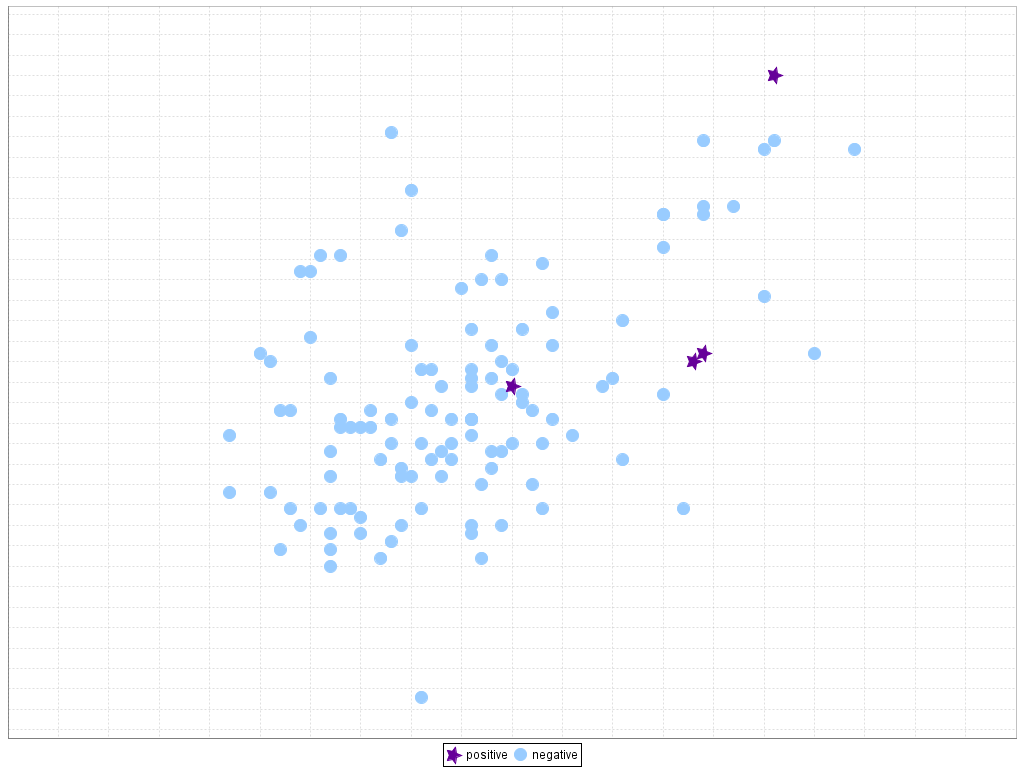
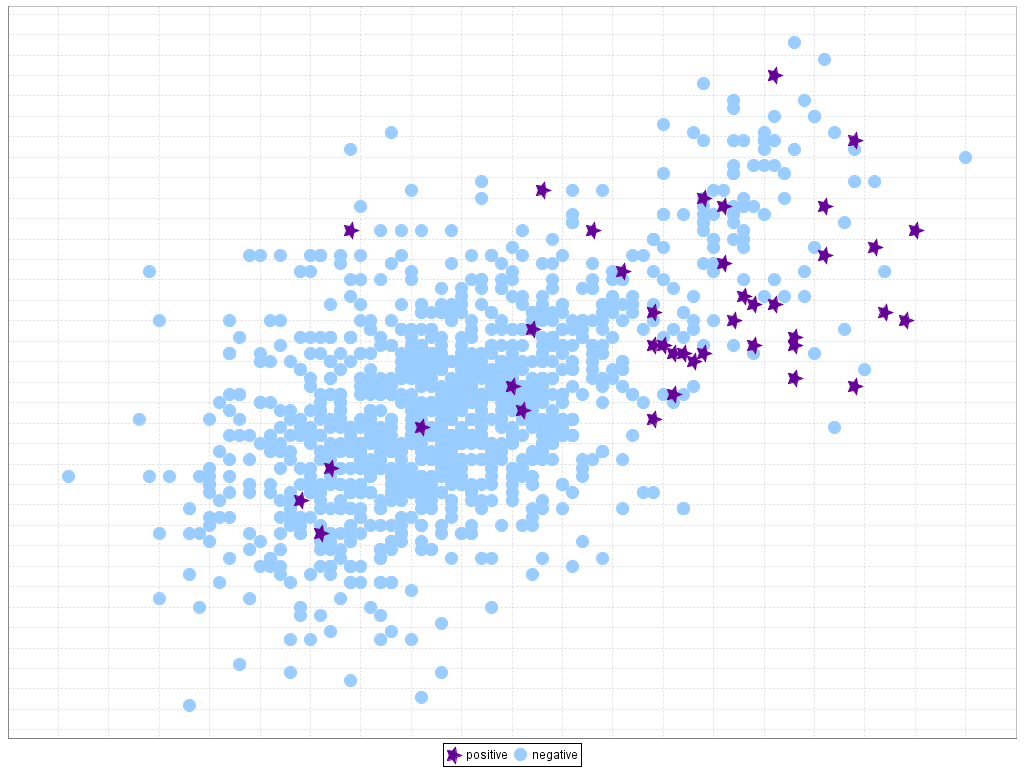
Figure 5. Lack of density or small sample size on the yeast4 dataset
The combination of imbalanced data and the small sample size problem presents a new challenge to the research community (M. Wasikowski, X.-W. Chen, Combating the small sample class imbalance problem using feature selection, IEEE Transactions on Knowledge and Data Engineering 22 (10) (2010) 1388–1400. doi: 10.1109/TKDE.2009.187). In this scenario, the minority class can be poorly represented and the knowledge model to learn this data space becomes too specific, leading to overfitting. Furthermore, as stated in the previous section, the lack of density in the training data may also cause the introduction of small disjuncts. Therefore, two datasets can not be considered to present the same complexity because they have the same IR, as it is also important how the training data represents the minority instances.
In G.M. Weiss, F.J. Provost, Learning when training data are costly: the effect of class distribution on tree induction, Journal of Artificial Intelligence Research 19 (2003) 315–354. doi: 10.1613/jair.1199, the authors have studied the effect of class distribution and training-set size on the classifier performance using C4.5 as base learning algorithm. Their analysis consisted in varying both the available training data and the degree of imbalance for several datasets and observing the differences for the AUC metric in those cases.
The first finding they extracted is somehow quite trivial, that is, the higher the number of training data, the better the performance results are, independently of the class distribution. A second important fact that they highlighted is that the IR that yields the best performances occasionally vary from one training-set size to another, giving the support to the notion that there may be a "best" marginal class distribution for a learning task and suggests that a progressive sampling algorithm may be useful in locating the class distribution that yields the best, or nearly best, classifier performance.
In order to visualize the effect of the density of examples in the learning process, in Figure 6 we show the results in AUC for the C4.5 classifier both for training (black line) and testing (grey line) for the vowel0 problem, varying the percentage of training instances from 10% to the original training size. This short experiment is carried out on a 5-fold cross validation, where the test data is not modified, i.e. in all cases it represents a 20% of the original data; the results shown are the average of the five partitions.
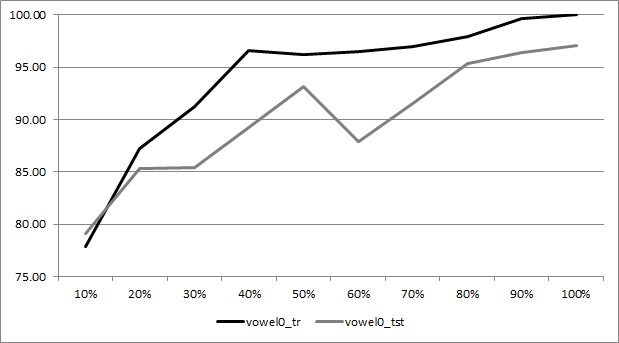
Figure 6. AUC performance for the C4.5 classifier with respect to the proportion of examples in the training set for the vowel0 problem
From this graph, we may distinguish a growth rate directly proportional to the number of training instances that are being used. This behavior reflects the findings enumerated previously from G.M. Weiss, F.J. Provost, Learning when training data are costly: the effect of class distribution on tree induction, Journal of Artificial Intelligence Research 19 (2003) 315–354. doi: 10.1613/jair.1199.
Class separability
The problem of overlapping between classes appears when a region of the data space contains a similar quantity of training data from each class. This situation leads to develop an inference with almost the same a priori probabilities in this overlapping area, which makes very hard or even impossible the distinction between the two classes. Indeed, any "linearly separable" problem can be solved by any simple classifier regardless of the class distribution.
There are several works which aim to study the relationship between overlapping and class imbalance. Particularly, in R.C. Prati, G.E.A.P.A., Batista, Class imbalances versus class overlapping: an analysis of a learning system behavior, in: Proceedings of the 2004 Mexican International Conference on Artificial Intelligence (MICAI'04), 2004, pp. 312–321 one can find a study where the authors propose several experiments with synthetic datasets varying the imbalance ratio and the overlap existing between the two classes. Their conclusions stated that the class probabilities are not the main responsibles for the hinder in the classification performance, but instead the degree of overlapping between the classes.
To reproduce the example for this scenario, we have created an artificial dataset with 1,000 examples having an IR of 9, i.e. 1 positive instance per 10 instances. Then, we have varied the degree of overlap for individual feature values, from no overlap to 100% of overlap, and we have used the C4.5 classifier in order to determine the influence of overlapping with respect to a fixed IR. First, Table 3 shows the results for the considered cases, where we observe that the performance is highly degrading with the increase of the overlap. Additionally, Figure 7 shows this issue, where we can observe that the decision tree is not only unable to obtain a correct discrimination between both classes when they are overlapped, but also that the preferred class is the majority one, leading to low values for the AUC metric.
| Overlap Degree (%) | TPrate | TNrate | AUC |
| 0% | 1.0000 | 1.0000 | 1.0000 |
| 20% | 0.7900 | 1.0000 | 0.8950 |
| 40% | 0.4900 | 1.0000 | 0.7450 |
| 50% | 0.4700 | 1.0000 | 0.7350 |
| 60% | 0.4200 | 1.0000 | 0.7100 |
| 80% | 0.2100 | 0.9989 | 0.6044 |
| 100% | 0.0000 | 1.0000 | 0.5000 |


Figure 7. Example of overlapping imbalanced datasets: boundaries detected by C4.5
Additionally, in V. García, R.A. Mollineda, J.S. Sánchez, On the k-NN performance in a challenging scenario of imbalance and overlapping, Pattern Analysis Applications 11 (3–4) (2008) 269–280. doi: 10.1007/s10044-007-0087-5, a similar study with several algorithms in different situations of imbalance and overlap focusing on the the kNN algorithm was developed. In this case, the authors proposed two different frameworks: on the one hand, they try to find the relation when the imbalance ratio in the overlap region is similar to the overall imbalance ratio whereas, on the other hand, they search for the relation when the imbalance ratio in the overlap region is inverse to the overall one (the positive class is locally denser than the negative class in the overlap region). They showed that when the overlapped data is not balanced, the IR in overlapping can be more important than the overlapping size. In addition, classifiers using a more global learning procedure attain greater TP rates whereas more local learning models obtain better TN rates than the former.
In M. Denil, T. Trappenberg, Overlap versus imbalance, in: Proceedings of the 23rd Canadian Conference on Advances in Artificial Intelligence (CCAI'10), Lecture Notes on Artificial Intelligence, vol. 6085, 2010, pp. 220–231, the authors examine the effects of overlap and imbalance on the complexity of the learned model and demonstrate that overlapping is a far more serious factor than imbalance in this respect. They demonstrate that these two problems acting in concert cause difficulties that are more severe than one would expect by examining their effects in isolation. In order to do so, they also use synthetic datasets for classifying with a SVM, where they vary the imbalance ratio, the overlap between classes and the imbalance ratio and overlap jointly. Their results show that, when the training set size is small, high levels of imbalance cause a dramatic drop in classifier performance, explained by the presence of small disjuncts. Overlapping classes cause a consistent drop in performance regardless of the size of the training set. However, with overlapping and imbalance combined, the classifier performance is degraded significantly beyond what the model predicts.
In one of the latest researches on the topic J. Luengo, A. Fernández, S. García, F. Herrera, Addressing data complexity for imbalanced data sets: analysis of SMOTE-based oversampling and evolutionary undersampling, Soft Computing 15 (10) (2011) 1909–1936. doi: 10.1007/s00500-010-0625-8, the authors have empirically extracted some interesting findings on real world datasets. Specifically, the authors depicted the performance of the different datasets ordered according to different data complexity measures (including the IR) in order to search for some regions of interesting good or bad behavior. They could not characterize any interesting behavior related to IR, but they do for other metrics that measure the overlap between the classes.
Finally, in R. Martín-Félez, R.A., Mollineda, On the suitability of combining feature selection and resampling to manage data complexity, in: Proceedings of the Conferencia de la Asociacion Española de Inteligencia Artificial (CAEPIA'09), Lecture Notes on Artificial Intelligence, vol. 5988, 2010, pp. 141–150, an approach that combines preprocessing and feature selection (strictly in this order) is proposed. This approach works in a way where preprocessing deals with class distribution and small disjuncts and feature selection somehow reduces the degree of overlapping. In a more general way, the idea behind this approach tries to overcome different sources of data complexity such as the class overlap, irrelevant and redundant features, noisy samples, class imbalance, low ratios of the sample size to dimensionality and so on, using different approaches used to solve each complexity.
Noisy data
Noisy data is known to affect the way any data mining system behaves (C.E. Brodley, M.A. Friedl, Identifying mislabeled training data, Journal of Artificial Intelligence Research 11 (1999) 131–167. doi: 10.1613/jair.606, J.A. Sáez, J. Luengo, F. Herrera, A first study on the noise impact in classes for fuzzy rule based classification systems, in: Proceedings of the 2010 IEEE International Conference on Intelligent Systems and Knowledge Engineering (ISKE'10), IEEE Press, 2010, pp. 153–158, X. Zhu, X. Wu, Class noise vs. attribute noise: a quantitative study, Artificial Intelligence Review 22 (3) (2004) 177–210. doi: 10.1007/s10462-004-0751-8). Focusing on the scenario of imbalanced data, the presence of noise has a greater impact on the minority classes than on usual cases (G.M. Weiss, Mining with rarity: a unifying framework, SIGKDD Explorations 6 (1) (2004) 7–19. doi: 10.1145/1007730.1007734); since the positive class has fewer examples to begin with, it will take fewer "noisy" examples to impact the learned subconcept. This issue is depicted in Figure 8, in which we can observe the decision boundaries obtained with SMOTE+C4.5 in the Subclus problem without noisy data and how the frontiers between the classes are wrongly generated by introducing a 20% gaussian noise.


Figure 8. Example of the effect of noise in imbalanced datasets for SMOTE+C4.5 in the Subclus dataset
According to G.M. Weiss, Mining with rarity: a unifying framework, SIGKDD Explorations 6 (1) (2004) 7–19. doi: 10.1145/1007730.1007734, these "noise-areas" can be somehow viewed as "small disjuncts" and in order to avoid the erroneous generation of discrimination functions for these examples, some overfitting management techniques must be employed, such as pruning. However, the handicap of this methodology is that some correct minority classes will be ignored and, in this manner, the bias of the learner should be tuned-up in order to be able to provide a good global behavior for both classes of the problem.
For example, Batuwita and Palade developed the FSVM-CIL algorithm (R. Batuwita, V. Palade, FSVM-CIL: fuzzy support vector machines for class imbalance learning, IEEE Transactions on Fuzzy Systems 18 (3) (2010) 558–571. doi: 10.1109/TFUZZ.2010.2042721), a synergy between SVMs and fuzzy logic aimed to reflect the within-class importance of different training examples in order to suppress the effect of outliers and noise. The idea is to assign different fuzzy membership values to positive and negative examples and to incorporate this information in the SVM learning algorithm, aimed to reduce the effect of outliers and noise when finding the separating hyperplane.
In C. Seiffert, T.M. Khoshgoftaar, J. Van Hulse, A. Folleco, An empirical study of the classification performance of learners on imbalanced and noisy software quality data, Information Sciences (2013), In press. doi: 10.1016/j.ins.2010.12.016 we may find an empirical study on the effect of class imbalance and class noise on different classification algorithms and data sampling techniques. From this study, the authors extracted three important lessons on the topic:
- Classification algorithms are more sensitive to noise than imbalance. However, as imbalance increases in severity, it plays a larger role in the performance of classifiers and sampling techniques.
- Regarding the preprocessing mechanisms, simple undersampling techniques such as random undersampling and ENN performed the best overall, at all levels of noise and imbalance. Peculiarly, as the level of imbalance is increased, ENN proves to be more robust in the presence of noise. Additionally, OSS consistently proves itself to be relatively unaffected by an increase in the noise level. Other techniques such as random oversampling, SMOTE or Borderline-SMOTE obtain good results on average, but do not show the same behavior as undersampling.
- Finally, the most robust classifiers tested over imbalanced and noisy data are bayesian classifiers and SVMs, performing better on average than rule induction algorithms or instance based learning. Furthermore, whereas most algorithms only experience small changes in AUC when imbalance was increased, the performance of Radial Basis Functions is significantly hindered when the imbalance ratio increases. For rule learning algorithms, the presence of noise degrades the performance more quickly than in other algorithms.
Additionally, in T.M. Khoshgoftaar, J. Van Hulse, A. Napolitano, Comparing boosting and bagging techniques with noisy and imbalanced data, IEEE Transactions on Systems, Man and Cybernetics, Part A: Systems and Humans 41 (3) (2011) 552–568. doi: 10.1109/TSMCA.2010.2084081, the authors presented a similar study on the significance of noise and imbalance data using bagging and boosting techniques. Their results show the goodness of the bagging approach without replacement, and they recommend the use of noise reduction techniques prior to the application of boosting procedures.
As a final remark, we show a brief experimental study on the effect of noise over a specific imbalanced problem such as the Subclus dataset (K. Napierala, J. Stefanowski, S. Wilk, Learning from imbalanced data in presence of noisy and borderline examples, in: Proceedings of the 7th International Conference on Rough Sets and Current Trends in Computing (RSCTC'10), Lecture Notes on Artificial Intelligence, vol. 6086, 2010, pp. 158–167.). Table 4 includes the results for C4.5 with no preprocessing (None) and four different approaches, namely random undersampling, SMOTE (N.V. Chawla, K.W. Bowyer, L.O. Hall, W.P. Kegelmeyer, SMOTE: synthetic minority over-sampling technique, Journal of Artificial Intelligent Research 16 (2002) 321–357. doi: 10.1613/jair.953), SMOTE+ENN (G.E.A.P.A. Batista, R.C. Prati, M.C. Monard, A study of the behaviour of several methods for balancing machine learning training data, SIGKDD Explorations 6 (1) (2004) 20–29. doi: 10.1145/1007730.1007735) and SPIDER2 (K. Napierala, J. Stefanowski, S. Wilk, Learning from imbalanced data in presence of noisy and borderline examples, in: Proceedings of the 7th International Conference on Rough Sets and Current Trends in Computing (RSCTC'10), Lecture Notes on Artificial Intelligence, vol. 6086, 2010, pp. 158–167.), a method designed for addressing noise and borderline examples, which will be detailed when discussing borderline examples.
This table is divided into two parts, the leftmost columns show the results with the original data and the columns in the right side show the results when adding a 20% of gaussian noise to the data. From this table we may conclude that in all cases the presence of noise degrades the performance of the classifier especially on the positive instances (TPrate). Regarding the preprocessing approaches, the best behavior is obtained by SMOTE+ENN and SPIDER2, both of which include a cleaning mechanism to alleviate the problem of noisy data, whereas the latter also oversample the borderline minority examples.
| Dataset | Original Data | 20% of Gaussian noise | ||||
| TPrate | TNrate | AUC | TPrate | TNrate | AUC | |
| None | 1.0000 | 0.9029 | 0.9514 | 0.0000 | 1.0000 | 0.5000 |
| RandomUnderSampling | 1.0000 | 0.7800 | 0.8900 | 0.9700 | 0.7400 | 0.8550 |
| SMOTE | 0.9614 | 0.9529 | 0.9571 | 0.8914 | 0.8800 | 0.8857 |
| SMOTE+ENN | 0.9676 | 0.9623 | 0.9649 | 0.9625 | 0.9573 | 0.9599 |
| SPIDER2 | 1.0000 | 1.0000 | 1.0000 | 0.9480 | 0.9033 | 0.9256 |
Borderline examples
Inspired by M. Kubat, S. Matwin, Addressing the curse of imbalanced training sets: one-sided selection, in: Proceedings of the 14th International Conference on Machine Learning (ICML'97), 1997, pp. 179–186, we may distinguish between safe, noisy and borderline examples. Safe examples are placed in relatively homogeneous areas with respect to the class label. By noisy examples we understand individuals from one class occurring in safe areas of the other class, as introduced in the previous section. Finally, Borderline examples are located in the area surrounding class boundaries, where the minority and majority classes overlap. Figure 9 represents two examples given by K. Napierala, J. Stefanowski, S. Wilk, Learning from imbalanced data in presence of noisy and borderline examples, in: Proceedings of the 7th International Conference on Rough Sets and Current Trends in Computing (RSCTC'10), Lecture Notes on Artificial Intelligence, vol. 6086, 2010, pp. 158–16., named "Paw and "Clover", respectively. In the former, the minority class is decomposed into 3 elliptic subregions, where two of them are located close to each other, and the remaining smaller sub-region is separated (upper right cluster). The latter also represents a non-linear setting, where the minority class resembles a flower with elliptic petals, which makes difficult to determine the boundaries examples in order to carry out a correct discrimination of the classes.
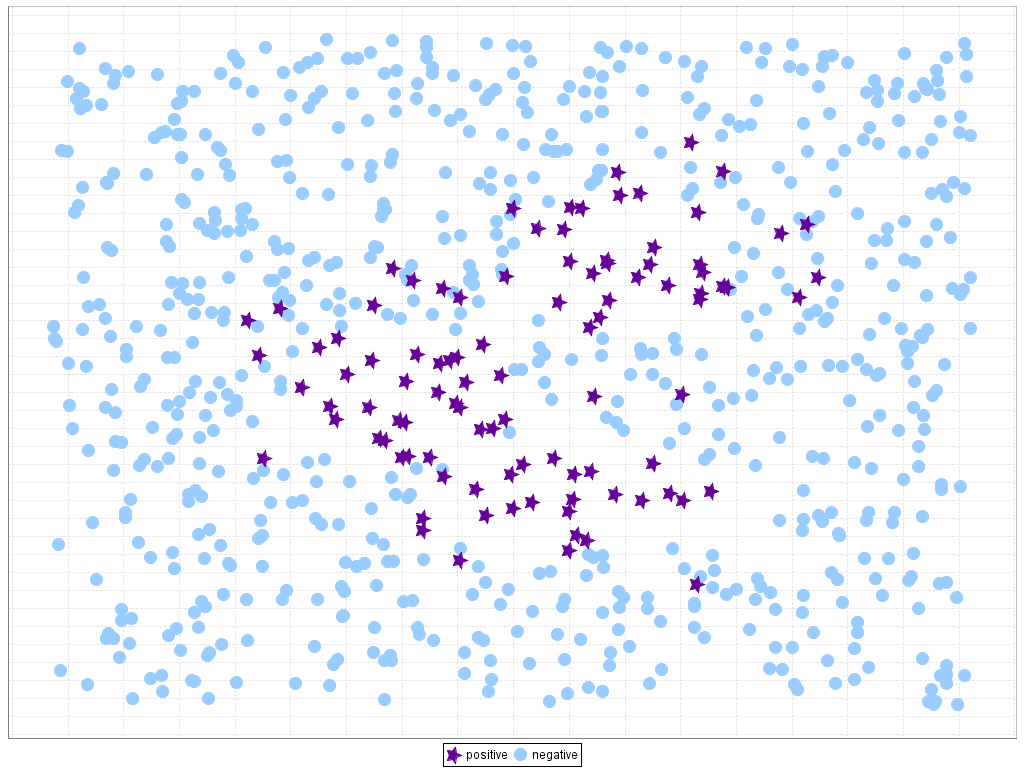
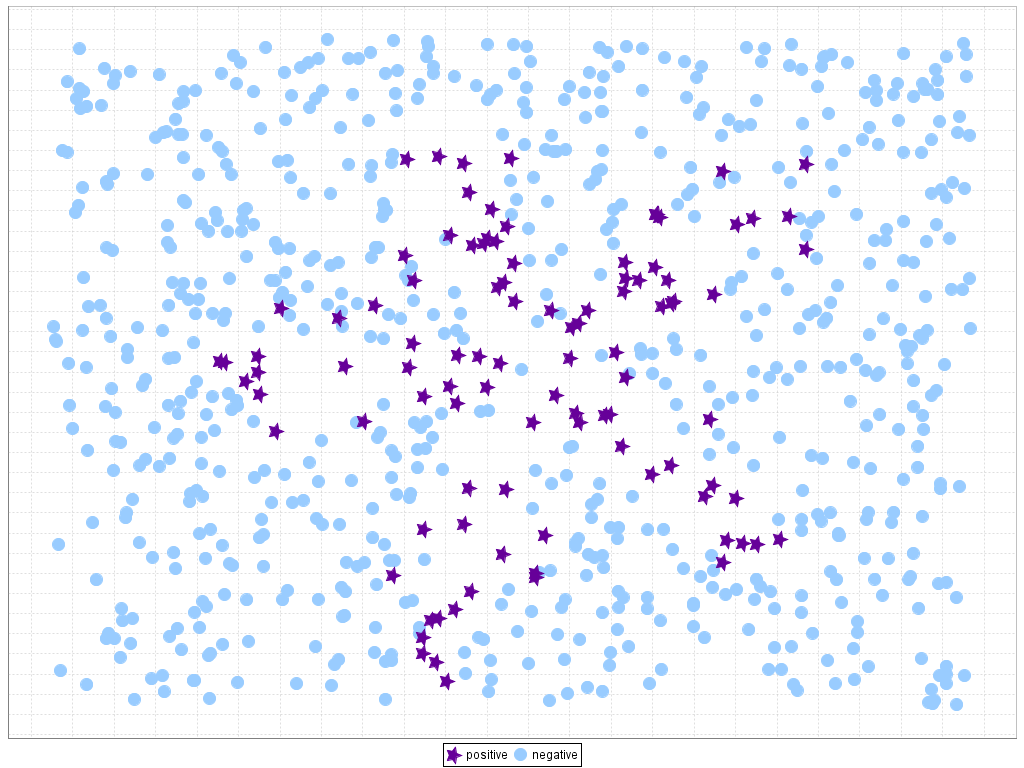
Figure 9. Example of data with difficult borderline examples
The problem of noisy data and the management of borderline examples are closely related, where the cleaning techniques can be used, or are the basis for detecting and emphasizing these borderline instances and, what is most important, to distinguish them from noisy instances that can degrade the overall classification. In brief, the better the definition of the borderline areas the more precise the discrimination between the positive and negative classes will be (D.J. Drown, T.M. Khoshgoftaar, N. Seliya, Evolutionary sampling and software quality modeling of high-assurance systems, IEEE Transactions on Systems, Man, and Cybernetics, Part A 39 (5) (2009) 1097–1107. doi: 10.1109/TSMCA.2009.2020804).
The family of SPIDER methods were proposed in J. Stefanowski, S. Wilk, Improving rule based classifiers induced by MODLEM by selective pre-processing of imbalanced data, in: Proceedings of the RSKD Workshop at ECML/PKDD'07, 2007, pp. 54–65 to ease the problem of the improvement of sensitivity at the cost of specificity that appears in the standard cleaning techniques. The SPIDER techniques works by combining a cleaning step of the majority examples with a local oversampling of the borderline minority examples (K. Napierala, J. Stefanowski, S. Wilk, Learning from imbalanced data in presence of noisy and borderline examples, in: Proceedings of the 7th International Conference on Rough Sets and Current Trends in Computing (RSCTC'10), Lecture Notes on Artificial Intelligence, vol. 6086, 2010, pp. 158–167, J. Stefanowski, S. Wilk, Improving rule based classifiers induced by MODLEM by selective pre-processing of imbalanced data, in: Proceedings of the RSKD Workshop at ECML/PKDD'07, 2007, pp. 54–65, J. Stefanowski, S. Wilk, Selective pre-processing of imbalanced data for improving classification performance, in: Proceedings of the 10th International Conference on Data Warehousing and Knowledge, Discovery (DaWaK08), 2008, pp. 283–292).
We may also find other related techniques such as the Borderline-SMOTE (H. Han, W.Y. Wang, B.H. Mao, Borderline–SMOTE: a new over–sampling method in imbalanced data sets learning, in: Proceedings of the 2005 International Conference on Intelligent Computing (ICIC'05), Lecture Notes in Computer Science, vol. 3644, 2005, pp. 878–887), which seeks to oversample the minority class instances in the borderline areas, by defining a set of "Danger" examples, i.e. those which are most likely to be misclassified since they appear in the borderline areas, from which SMOTE generates synthetic minority samples in the neighborhood of the boundaries.
Other approaches such as Safe-Level-SMOTE (C. Bunkhumpornpat, K. Sinapiromsaran, C. Lursinsap, Safe–level–SMOTE: Safe–level–synthetic minority over–sampling TEchnique for handling the class imbalanced problem. In: Proceedings of the 13th Pacific–Asia Conference on Advances in Knowledge Discovery and Data Mining PAKDD'09, 2009, pp. 475–482) and ADASYN (H. He, Y. Bai, E.A. Garcia, S. Li, ADASYN: adaptive synthetic sampling approach for imbalanced learning, in: Proceedings of the 2008 IEEE International Joint Conference on Neural Networks (IJCNN'08), 2008, pp. 1322–1328) work in a similar way. The former is based on the premise that previous approaches, such as SMOTE and Borderline-SMOTE, may generate synthetic instances in unsuitable locations, such as overlapping regions and noise regions; therefore, the authors compute a "safe-level" value for each positive instance before generating synthetic instances and generate them closer to the largest safe level. On the other hand, the key idea of the ADASYN algorithm is to use a density distribution as a criterion to automatically decide the number of synthetic samples that need to be generated for each minority example, by adaptively changing the weights of different minority examples to compensate the skewed distributions.
In V. López, A. Fernández, M.J. del Jesus, F. Herrera, A hierarchical genetic fuzzy system based on genetic programming for addressing classification with highly imbalanced and borderline data-sets, Knowledge-Based Systems 38 (2013) 85–104. doi: 10.1016/j.knosys.2012.08.025, the authors use a hierarchical fuzzy rule learning approach, which defines a higher granularity for those problem subspaces in the borderline areas. The results have shown to be very competitive for highly imbalanced datasets in which this problem is accentuated.
Finally, in K. Napierala, J. Stefanowski, S. Wilk, Learning from imbalanced data in presence of noisy and borderline examples, in: Proceedings of the 7th International Conference on Rough Sets and Current Trends in Computing (RSCTC'10), Lecture Notes on Artificial Intelligence, vol. 6086, 2010, pp. 158–167, the authors presented a series of experiments in which it is shown that the degradation in performance of a classifier is strongly affected by the number of borderline examples. They showed that focused resampling mechanisms (such as the Neighborhood Cleaning Rule (J. Laurikkala, Improving identification of difficult small classes by balancing class distribution, in: Proceedings of the 8th Conference on AI in Medicine in Europe: Artificial Intelligence Medicine (AIME'01), 2001, pp. 63–66) or SPIDER2 (K. Napierala, J. Stefanowski, S. Wilk, Learning from imbalanced data in presence of noisy and borderline examples, in: Proceedings of the 7th International Conference on Rough Sets and Current Trends in Computing (RSCTC'10), Lecture Notes on Artificial Intelligence, vol. 6086, 2010, pp. 158–167)) work well when the number of borderline examples is large enough whereas, on the contrary case, oversampling methods allow the improvement of the precision for the minority class.
The behavior of the SPIDER2 approach is shown in Table 5 for both the Paw and Clover problems. There are 10 different problems for each one of these datasets, depending on the number of examples and IR (600-5 or 800-7), and the "disturbance ratio" (K. Napierala, J. Stefanowski, S. Wilk, Learning from imbalanced data in presence of noisy and borderline examples, in: Proceedings of the 7th International Conference on Rough Sets and Current Trends in Computing (RSCTC'10), Lecture Notes on Artificial Intelligence, vol. 6086, 2010, pp. 158–167), defined as the ratio of borderline examples from the minority class subregions (0 to 70%). From these results we must stress the goodness of the SPIDER2 preprocessing step especially for those problems with a high disturbance ratio, which are harder to solve.
| Dataset | Disturbance | 600 examples - IR 5 | 800 examples - IR 7 | ||||||
| None | SPIDER2 | None | SPIDER2 | ||||||
| AUCTr | AUCTst | AUCTr | AUCTst | AUCTr | AUCTst | AUCTr | AUCTst | ||
| Paw | 0 | 0.9568 | 0.9100 | 0.9418 | 0.9180 | 0.7095 | 0.6829 | 0.9645 | 0.9457 |
| 30 | 0.7298 | 0.7000 | 0.9150 | 0.8260 | 0.6091 | 0.5671 | 0.9016 | 0.8207 | |
| 50 | 0.7252 | 0.6790 | 0.9055 | 0.8580 | 0.5000 | 0.5000 | 0.9114 | 0.8400 | |
| 60 | 0.5640 | 0.5410 | 0.9073 | 0.8150 | 0.5477 | 0.5300 | 0.8954 | 0.7829 | |
| 70 | 0.6250 | 0.5770 | 0.8855 | 0.8350 | 0.5000 | 0.5000 | 0.8846 | 0.8164 | |
| Average | 0.7202 | 0.6814 | 0.9110 | 0.8504 | 0.5732 | 0.5560 | 0.9115 | 0.8411 | |
| Clover | 0 | 0.7853 | 0.7050 | 0.7950 | 0.7410 | 0.7607 | 0.7071 | 0.8029 | 0.7864 |
| 30 | 0.6153 | 0.5430 | 0.9035 | 0.8290 | 0.5546 | 0.5321 | 0.8948 | 0.7979 | |
| 50 | 0.5430 | 0.5160 | 0.8980 | 0.8070 | 0.5000 | 0.5000 | 0.8823 | 0.7907 | |
| 60 | 0.5662 | 0.5650 | 0.8798 | 0.8100 | 0.5000 | 0.5000 | 0.8848 | 0.8014 | |
| 70 | 0.5000 | 0.5000 | 0.8788 | 0.7690 | 0.5250 | 0.5157 | 0.8787 | 0.7557 | |
| Average | 0.6020 | 0.5658 | 0.8710 | 0.7912 | 0.5681 | 0.5510 | 0.8687 | 0.7864 | |
Additionally, and as a visual example of the behavior of this kind of methods, we show in Figures 10 and 11 the classification regions detected with C4.5 for the Paw and Clover problems using the original data and applying the SPIDER2 method. From these results we may conclude that the use of a methodology for stressing the borderline areas is very beneficial for correctly identifying the minority class instances.


Figure 10. Boundaries detected by C4.5 in the Paw problem (800 examples, IR 7 and disturbance ratio of 30)


Figure 11. Boundaries detected by C4.5 in the Clover problem (800 examples, IR 7 and disturbance ratio of 30)
Dataset shift
The problem of dataset shift (R. Alaiz-Rodríguez, N. Japkowicz, Assessing the impact of changing environments on classifier performance, in: Proceedings of the 21st Canadian Conference on Advances in Artificial Intelligence (CCAI’08), Springer-Verlag, Berlin, Heidelberg, 2008, pp. 13–24, J.Q. Candela, M. Sugiyama, A. Schwaighofer, N.D. Lawrence, Dataset Shift in Machine Learning, The MIT Press, 2009, H. Shimodaira, Improving predictive inference under covariate shift by weighting the log-likelihood function, Journal of Statistical Planning and Inference 90 (2) (2000) 227–244. doi: 10.1016/S0378-3758(00)00115-4) is defined as the case where training and test data follow different distributions. This is a common problem that can affect all kind of classification problems, and it often appears due to sample selection bias issues. A mild degree of dataset shift is present in most real-world problems, but general classifiers are often capable of handling it without a severe performance loss.
However, the dataset shift issue is specially relevant when dealing with imbalanced classification, because in highly imbalanced domains, the minority class is particularly sensitive to singular classification errors, due to the typically low number of examples it presents (J.G. Moreno-Torres, F. Herrera, A preliminary study on overlapping and data fracture in imbalanced domains by means of genetic programming-based feature extraction, in: Proceedings of the 10th International Conference on Intelligent Systems Design and Applications (ISDA’10), 2010, pp. 501–506). In the most extreme cases, a single misclassified example of the minority class can create a significant drop in performance.
For clarity, Figures 12 and 13 present two examples of the influence of the dataset shift in imbalanced classification. In the first case (Figure 12), it is easy to see a separation between classes in the training set that carries over perfectly to the test set. However, in the second case (Figure 13), it must be noted how some minority class examples in the test set are at the bottom and rightmost areas while they are localized in other areas in the training set, leading to a gap between the training and testing performance. These problems are represented in a two-dimensional space by means of a linear transformation of the inputs variables, following the technique given in J.G. Moreno-Torres, F. Herrera, A preliminary study on overlapping and data fracture in imbalanced domains by means of genetic programming-based feature extraction, in: Proceedings of the 10th International Conference on Intelligent Systems Design and Applications (ISDA’10), 2010, pp. 501–506.
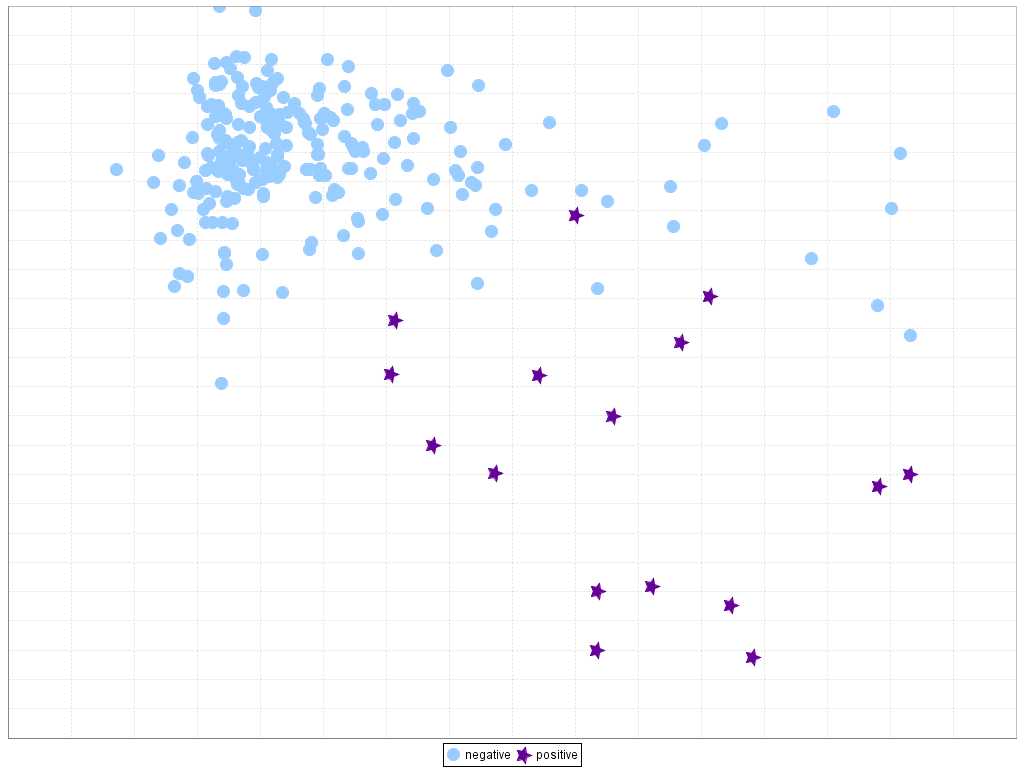
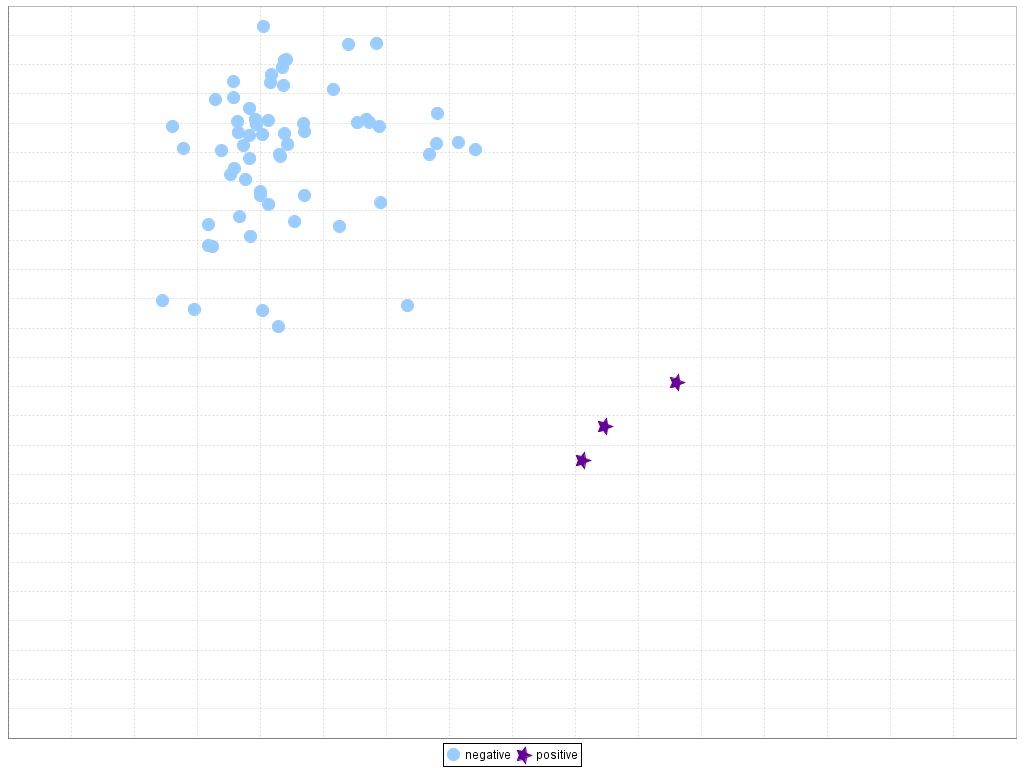
Figure 12. Example of good behavior (no dataset shift) in imbalanced domains: ecoli4 dataset, 5th partition
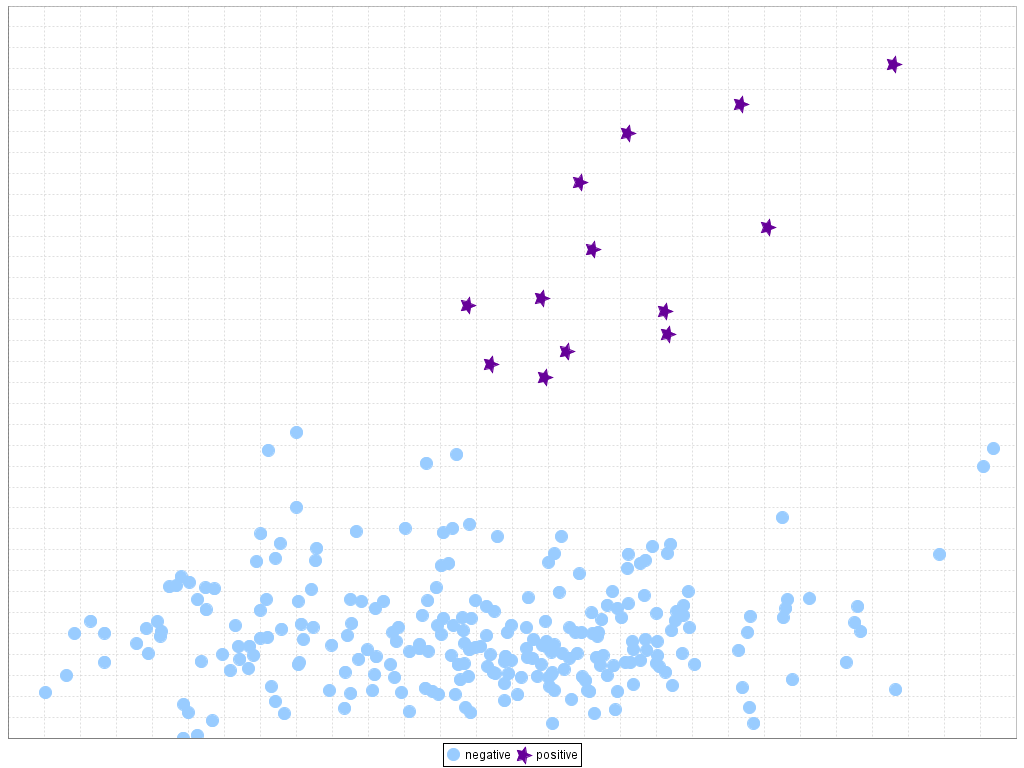
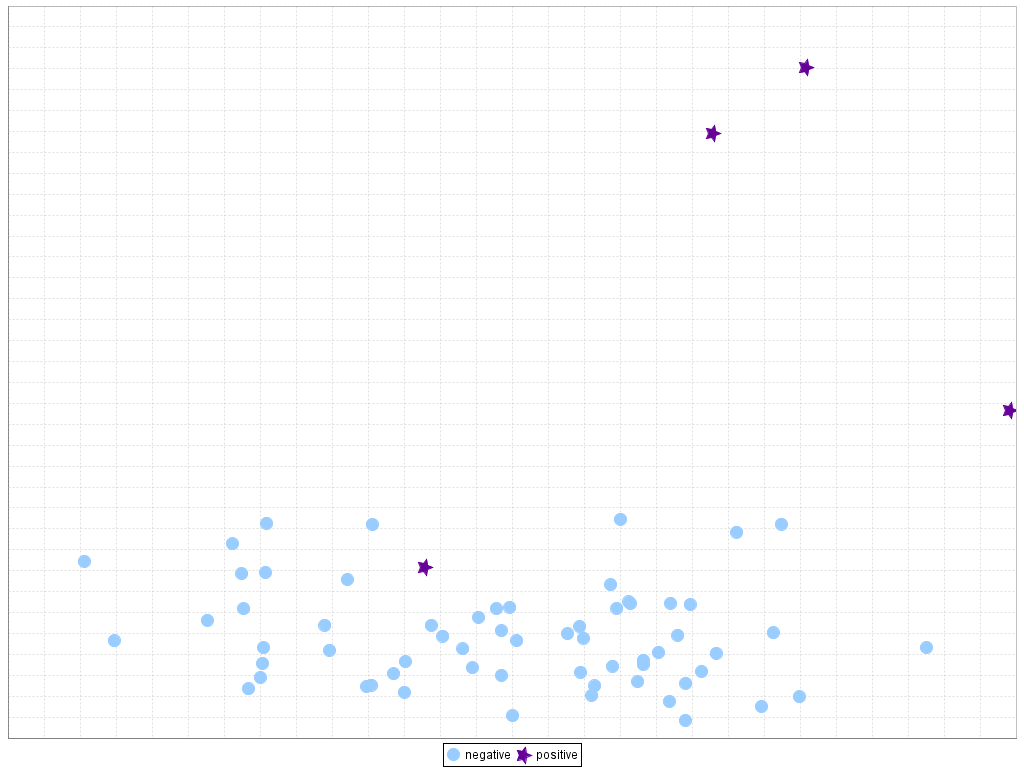
Figure 13. Example of bad behavior caused by dataset shift in imbalanced domains: ecoli4 dataset, 1st partition
Since the dataset shift is a highly relevant issue in imbalanced classification, it is easy to see why it would be an interesting perspective to focus on in future research regarding this topic. There are two different potential approaches in the study of the dataset shift in imbalanced domains:
- The first one focuses on intrinsic dataset shift, that is, the data of interest includes some degree of shift that is producing a relevant drop in performance. In this case, we may develop techniques to discover and measure the presence of dataset shift (D.A. Cieslak, N.V. Chawla, Analyzing pets on imbalanced datasets when training and testing class distributions differ, in: Proceedings of the Pacific-Asia Conference on Knowledge Discovery and Data Mining (PAKDD08). Osaka, Japan, 2008, pp. 519–526, D.A. Cieslak, N.V. Chawla, A framework for monitoring classifiers’ performance: when and why failure occurs?, Knowledge and Information Systems 18 (1) (2009) 83–108. doi: 10.1007/s10115-008-0139-1, Y. Yang, X. Wu, X. Zhu, Conceptual equivalence for contrast mining in classification learning, Data & Knowledge Engineering 67 (3) (2008) 413–429. doi: 10.1016/j.datak.2008.07.001), but adapting them to focus on the minority class. Furthermore, we may design algorithms that are capable of working under dataset shift conditions, either by means of preprocessing techniques (J.G. Moreno-Torres, X. Llorà, D.E. Goldberg, R. Bhargava, Repairing fractures between data using genetic programming-based feature extraction: a case study in cancer diagnosis, Information Sciences 222 (2013) 805–823. doi: 10.1016/j.ins.2010.09.018) or with ad hoc algorithms (R. Alaiz-Rodríguez, A. Guerrero-Curieses, J. Cid-Sueiro, Improving classification under changes in class and within-class distributions, in: Proceedings of the 10th International Work-Conference on Artificial Neural Networks (IWANN ’09), Springer-Verlag, Berlin, Heidelberg, 2009, pp. 122–130, S. Bickel, M. Brückner, T. Scheffer, Discriminative learning under covariate shift, Journal of Machine Learning Research 10 (2009) 2137–2155. doi: 10.1145/1577069.1755858, A. Globerson, C.H. Teo, A. Smola, S. Roweis, An adversarial view of covariate shift and a minimax approach, in: J. Quiñonero Candela, M. Sugiyama, A. Schwaighofer, N.D. Lawrence (Eds.), Dataset Shift in Machine Learning, The MIT Press, 2009, pp. 179–198). In both cases, we are not aware of any proposals in the literature that focus on the problem of imbalanced classification in the presence of dataset shift.
- The second approach in terms of dataset shift in imbalanced classification is related to induced dataset shift. Most current state of the art research is validated through stratified cross-validation techniques, which are another potential source of shift in the learning process. A more suitable validation technique needs to be developed in order to avoid introducing dataset shift issues artificially.
Addressing Classification with imbalanced data: preprocessing, cost-sensitive learning and ensemble techniques
A large number of approaches have been proposed to deal with the class imbalance problem. These approaches can be categorized into two groups: the internal approaches that create new algorithms or modify existing ones to take the class-imbalance problem into consideration (R. Barandela, J.S. Sánchez, V. García, E. Rangel, Strategies for learning in class imbalance problems, Pattern Recognition 36 (3) (2003) 849–851. doi: 10.1016/S0031-3203(02)00257-1, P. Ducange, B. Lazzerini, F. Marcelloni, Multi-objective genetic fuzzy classifiers for imbalanced and cost-sensitive datasets, Soft Computing 14 (7) (2010) 713–728. doi: 10.1007/s00500-009-0460-y, W. Lin, J.J. Chen, Class-imbalanced classifiers for high-dimensional data, Briefings in Bioinformatics 14 (1) (2013) 13–26. doi: 10.1093/bib/bbs006, J. Wang, J. You, Q. Li, Y. Xu, Extract minimum positive and maximum negative features for imbalanced binary classification, Pattern Recognition 45 (3) (2012) 1136–1145. doi: 10.1016/j.patcog.2011.09.004, W. Zong, G.-B. Huang, Y. Chen, Weighted extreme learning machine for imbalance learning, Neurocomputing 101 (2013) 229–242. doi: 10.1016/j.neucom.2012.08.010) and external approaches that preprocess the data in order to diminish the effect of their class imbalance (G.E.A.P.A. Batista, R.C. Prati, M.C. Monard, A study of the behaviour of several methods for balancing machine learning training data, SIGKDD Explorations 6 (1) (2004) 20–29. doi: 10.1145/1007730.1007735, A. Estabrooks, T. Jo, N. Japkowicz, A multiple resampling method for learning from imbalanced data sets, Computational Intelligence 20 (1) (2004) 18–36. doi: 10.1111/j.0824-7935.2004.t01-1-00228.x). Furthermore, cost-sensitive learning solutions incorporating both the data (external) and algorithmic level (internal) approaches assume higher misclassification costs for samples in the minority class and seek to minimize the high cost errors (R. Batuwita, V. Palade, Class imbalance learning methods for support vector machines, in: H. He, Y. Ma (Eds.), Imbalanced Learning: Foundations, Algorithms, and Applications, Wiley, 2013, pp. 83–96., P. Domingos, Metacost: a general method for making classifiers cost–sensitive, in: Proceedings of the 5th International Conference on Knowledge Discovery and Data Mining (KDD’99), 1999, pp. 155–164., N. García-Pedrajas, J. Pérez-Rodríguez, M. García-Pedrajas, D. Ortiz-Boyer, C. Fyfe, Class imbalance methods for translation initiation site recognition in DNA sequences, Knowledge Based Systems 25 (1) (2012) 22–34. doi: 10.1016/j.knosys.2011.05.002, Z.-H. Zhou, X.-Y. Liu, Training cost-sensitive neural networks with methods addressing the class imbalance problem, IEEE Transactions on Knowledge and Data Engineering 18 (1) (2006) 63–77. doi: 10.1109/TKDE.2006.17). Ensemble methods (R. Polikar, Ensemble based systems in decision making, IEEE Circuits and Systems Magazine 6 (3) (2006) 21–45. doi: 10.1109/MCAS.2006.1688199, L. Rokach, Ensemble-based classifiers, Artificial Intelligence Review 33 (1) (2010) 1–39. doi: 10.1007/s10462-009-9124-7) are also frequently adapted to imbalanced domains, either by modifying the ensemble learning algorithm at the data-level approach to preprocess the data before the learning stage of each classifier (J. Blaszczynski, M. Deckert, J. Stefanowski, S. Wilk, Integrating selective pre-processing of imbalanced data with ivotes ensemble, in: M. Szczuka, M. Kryszkiewicz, S. Ramanna, R. Jensen, Q. Hu (Eds.), Rough Sets and Current Trends in Computing, LNCS, vol. 6086, Springer, Berlin/Heidelberg, 2010, pp. 148–157., N.V. Chawla, A. Lazarevic, L.O. Hall, K.W. Bowyer, SMOTEBoost: Improving prediction of the minority class in boosting, in: Proceedings of 7th European Conference on Principles and Practice of Knowledge Discovery in Databases (PKDD’03), 2003, pp. 107–119., C. Seiffert, T.M. Khoshgoftaar, J. Van Hulse, A. Napolitano, RUSBoost: a hybrid approach to alleviating class imbalance, IEEE Transactions on System, Man and Cybernetics A 40 (1) (2010) 185–197. doi: 10.1109/TSMCA.2009.2029559) or by embedding a cost-sensitive framework in the ensemble learning process (W. Fan, S.J. Stolfo, J. Zhang, P.K. Chan, Adacost: misclassification cost-sensitive boosting, in: Proceedings of the 16th International Conference on Machine Learning (ICML’96), Morgan Kaufmann Publishers Inc., San Francisco, CA, USA, 1999, pp. 97–105., Y. Sun, M.S. Kamel, A.K.C. Wong, Y. Wang, Cost-sensitive boosting for classification of imbalanced data, Pattern Recognition 40 (12) (2007) 3358–3378. doi: 10.1016/j.patcog.2007.04.009, K.M. Ting, A comparative study of cost-sensitive boosting algorithms, in: Proceedings of the 17th International Conference on Machine Learning (ICML’00), Stanford, CA, USA, 2000, pp. 983–990.).
Preprocessing imbalanced datasets: resampling techniques
In the specialized literature, we can find some papers about resampling techniques studying the effect of changing the class distribution in order to deal with imbalanced datasets.
Those works have proved empirically that applying a preprocessing step in order to balance the class distribution is usually an useful solution (G.E.A.P.A. Batista, R.C. Prati, M.C. Monard, A study of the behaviour of several methods for balancing machine learning training data, SIGKDD Explorations 6 (1) (2004) 20–29. doi: 10.1145/1007730.1007735, R. Batuwita, V. Palade, Efficient resampling methods for training support vector machines with imbalanced datasets, in: Proceedings of the 2010 International Joint Conference on Neural Networks (IJCNN), 2010., A. Fernández, M.J. del Jesus, F. Herrera, On the 2-tuples based genetic tuning performance for fuzzy rule based classification systems in imbalanced data-sets, Information Sciences 180 (8) (2010) 1268–1291. doi: 10.1016/j.ins.2009.12.014, A. Fernández, S. García, M.J. del Jesus, F. Herrera, A study of the behaviour of linguistic fuzzy rule based classification systems in the framework of imbalanced data-sets, Fuzzy Sets and Systems 159 (18) (2008) 2378–2398. doi: 10.1016/j.fss.2007.12.023. Furthermore, the main advantage of these techniques is that they are independent of the underlying classifier.
Resampling techniques can be categorized into three groups or families:
- Undersampling methods, which create a subset of the original dataset by eliminating instances (usually majority class instances).
- Oversampling methods, which create a superset of the original dataset by replicating some instances or creating new instances from existing ones.
- Hybrids methods, which combine both sampling approaches from above.
Within these families of methods, the simplest preprocessing techniques are non-heuristic methods such as random undersampling and random oversampling. In the first case, the major drawback is that it can discard potentially useful data, that could be important for the learning process. For random oversampling, several authors agree that this method can increase the likelihood of occurring overfitting, since it makes exact copies of existing instances.
In order to deal with the mentioned problems, more sophisticated methods have been proposed. Among them, the "Synthetic Minority Oversampling TEchnique" (SMOTE) (N.V. Chawla, K.W. Bowyer, L.O. Hall, W.P. Kegelmeyer, SMOTE: synthetic minority over-sampling technique, Journal of Artificial Intelligent Research 16 (2002) 321–357. doi: 10.1613/jair.953) has become one of the most renowned approaches in this area. In brief, its main idea is to create new minority class examples by interpolating several minority class instances that lie together for oversampling the training set.
With this technique, the positive class is over-sampled by taking each minority class sample and introducing synthetic examples along the line segments joining any/all of the k minority class nearest neighbors. Depending upon the amount of over-sampling required, neighbors from the k nearest neighbors are randomly chosen. This process is illustrated in Fig. X, where xi is the selected point, xi1 to xi4 are some selected nearest neighbors and r1 to r4 the synthetic data points created by the randomized interpolation.
Figure 14. An illustration of how to create the synthetic data points in the SMOTE algorithm
However, in oversampling techniques, and especially for the SMOTE algorithm, the problem of over generalization is largely attributed to the way in which synthetic samples are created. Precisely, SMOTE generates the same number of synthetic data samples for each original minority example and does so without consideration to neighboring examples, which increases the occurrence of overlapping between classes (B.X. Wang, N. Japkowicz, Imbalanced data set learning with synthetic samples, in: Proceedings of the IRIS Machine Learning Workshop, 2004.). To this end, various adaptive sampling methods have been proposed to overcome this limitation; some representative works include the Borderline-SMOTE (H. Han, W.Y. Wang, B.H. Mao, Borderline–SMOTE: a new over–sampling method in imbalanced data sets learning, in: Proceedings of the 2005 International Conference on Intelligent Computing (ICIC’05), Lecture Notes in Computer Science, vol. 3644, 2005, pp. 878–887.), Adaptive Synthetic Sampling (H. He, Y. Bai, E.A. Garcia, S. Li, ADASYN: adaptive synthetic sampling approach for imbalanced learning, in: Proceedings of the 2008 IEEE International Joint Conference on Neural Networks (IJCNN’08), 2008, pp. 1322–1328.), Safe-Level-SMOTE (C. Bunkhumpornpat, K. Sinapiromsaran, C. Lursinsap, Safe–level–SMOTE: Safe–level–synthetic minority over–sampling TEchnique for handling the class imbalanced problem. In: Proceedings of the 13th Pacific–Asia Conference on Advances in Knowledge Discovery and Data Mining PAKDD’09, 2009, pp. 475–482.) and SPIDER2 (J. Stefanowski, S. Wilk, Selective pre-processing of imbalanced data for improving classification performance, in: Proceedings of the 10th International Conference on Data Warehousing and Knowledge, Discovery (DaWaK08), 2008, pp. 283–292.) algorithms.
Regarding undersampling, most of the proposed approaches are based on data cleaning techniques. Some representative works in this area include the Wilson's edited nearest neighbor (ENN) (D.L. Wilson, Asymptotic properties of nearest neighbor rules using edited data, IEEE Transactions on Systems, Man and Cybernetics 2 (3) (1972) 408–421. doi: 10.1109/TSMC.1972.4309137) rule, which removes examples that differ from two of its three nearest neighbors, the one-sided selection (OSS) (M. Kubat, S. Matwin, Addressing the curse of imbalanced training sets: one-sided selection, in: Proceedings of the 14th International Conference on Machine Learning (ICML’97), 1997, pp. 179–186.), an integration method between the condensed nearest neighbor rule (P.E. Hart, The condensed nearest neighbor rule, IEEE Transactions on Information Theory 14 (1968) 515–516. doi: 10.1109/TIT.1968.1054155) and Tomek Links (I. Tomek, Two modifications of CNN, IEEE Transactions on Systems Man and Communications 6 (1976) 769–772. doi: 10.1109/TSMC.1976.4309452) and the neighborhood cleaning rule (J. Laurikkala, Improving identification of difficult small classes by balancing class distribution, in: Proceedings of the 8th Conference on AI in Medicine in Europe: Artificial Intelligence Medicine (AIME’01), 2001, pp. 63–66.), which is based on the ENN technique. Additionally, the NearMiss-2 method (J. Zhang, I. Mani, KNN approach to unbalanced data distributions: a case study involving information extraction, in: Proceedings of the 20th International Conference on Machine Learning (ICML’03), Workshop Learning from Imbalanced Data Sets, 2003.) selects the majority class examples whose average distance to the three farthest minority class examples is the smallest, and in (A. Anand, G. Pugalenthi, G.B. Fogel, P.N. Suganthan, An approach for classification of highly imbalanced data using weighting and undersampling, Amino Acids 39 (5) (2010) 1385–1391. doi: 10.1007/s00726-010-0595-2) the authors proposed a method that removes the majority instances far from the decision boundaries. Furthermore, a Support Vector Machine (SVM) (C. Cortes, V. Vapnik, Support vector networks, Machine Learning 20 (1995) 273–297. doi: 10.1007/BF00994018) may be used to discard redundant or irrelevant majority class examples (Y. Tang, Y.-Q. Zhang, N.V. Chawla, S. Kresser, SVMs modeling for highly imbalanced classification, IEEE Transactions on Systems, Man and Cybernetics, Part B 39 (1) (2009) 281–288. doi: 10.1109/TSMCB.2008.2002909). Finally, the combination of preprocessing of instances with data cleaning techniques could lead to diminishing the overlapping that is introduced by sampling methods, i.e. the integrations of SMOTE with ENN and SMOTE with Tomek links (G.E.A.P.A. Batista, R.C. Prati, M.C. Monard, A study of the behaviour of several methods for balancing machine learning training data, SIGKDD Explorations 6 (1) (2004) 20–29. doi: 10.1145/1007730.1007735). This behavior is also present in a wrapper technique introduced in (N.V. Chawla, D.A. Cieslak, L.O. Hall, A. Joshi, Automatically countering imbalance and its empirical relationship to cost, Data Mining and Knowledge Discovery 17 (2) (2008) 225–252. doi: 10.1007/s10618-008-0087-0) that defines the best percentage to perform both undersampling and oversampling.
On the other hand, these techniques are not only carried out by means of a "neighborhood", but we must also stress some cluster-based sampling algorithms, all of which aim to organize the training data into groups with significant characteristics and then performing both undersampling and/or oversampling. Some significant examples are the Cluster-Based Oversampling (CBO) (T. Jo, N. Japkowicz, Class imbalances versus small disjuncts, ACM SIGKDD Explorations Newsletter 6 (1) (2004) 40–49. doi: 10.1145/1007730.1007737), Class Purity Maximization (K. Yoon, S. Kwek, An unsupervised learning approach to resolving the data imbalanced issue in supervised learning problems in functional genomics, in: Proceedings of the 5th International Conference on Hybrid Intelligent Systems (HIS’05), 2005, pp. 303–308.), Sampling-Based Clustering (S. Yen, Y. Lee, Under-sampling approaches for improving prediction of the minority class in an imbalanced dataset, in: Proceedings of the 2006 International Conference on Intelligent, Computing (ICIC06), 2006, pp. 731–740.), the agglomerative Hierarchical Clustering (G. Cohen, M. Hilario, H. Sax, S. Hugonnet, A. Geissbuhler, Learning from imbalanced data in surveillance of nosocomial infection, Artificial Intelligence in Medicine 37 (2006) 7–18. doi: 10.1016/j.artmed.2005.03.002) or the DBSMOTE algorithm based on DBSCAN clustering (C. Bunkhumpornpat, K. Sinapiromsaran, C. Lursinsap, DBSMOTE: density-based synthetic minority over-sampling technique, Applied Intelligence 36 (3) (2012) 664–684. doi: 10.1007/s10489-011-0287-y).
Finally, the application of genetic algorithms or particle swarm optimization for the correct identification of the most useful instances has shown to achieve good results (S. García, F. Herrera, Evolutionary under-sampling for classification with imbalanced data sets: proposals and taxonomy, Evolutionary Computation 17 (3) (2009) 275–306. doi: 10.1162/evco.2009.17.3.275, P. Yang, L. Xu, B.B. Zhou, Z. Zhang, A.Y. Zomaya, A particle swarm based hybrid system for imbalanced medical data sampling, BMC Genomics 10 (Suppl. 3) (2009). art. no. S34.. doi: 10.1186/1471-2164-10-S3-S34). Also, a training set selection can be carried out in the area of imbalanced datasets (S. García, J. Derrac, I. Triguero, C.J. Carmona, F. Herrera, Evolutionary-based selection of generalized instances for imbalanced classification, Knowledge Based Systems 25 (1) (2012) 3–12. doi: 10.1016/j.knosys.2011.01.012, S. García, A. Fernández, F. Herrera, Enhancing the effectiveness and interpretability of decision tree and rule induction classifiers with evolutionary training set selection over imbalanced problems, Applied Soft Computing 9 (2009) 1304–1314. doi: 10.1016/j.asoc.2009.04.004). These methods select the best set of examples to improve the behavior of several algorithms considering for this purpose the classification performance using an appropriate imbalanced measure.
Cost-sensitive learning
Cost-sensitive learning takes into account the variable cost of a misclassification with respect to the different classes (P. Domingos, Metacost: a general method for making classifiers cost–sensitive, in: Proceedings of the 5th International Conference on Knowledge Discovery and Data Mining (KDD’99), 1999, pp. 155–164., B. Zadrozny, J. Langford, N. Abe, Cost–sensitive learning by cost–proportionate example weighting, in: Proceedings of the 3rd IEEE International Conference on Data Mining (ICDM’03), 2003, pp. 435–442.). In this case, a cost matrix codifies the penalties C(i,j) of classifying examples of one class i as a different one j, as illustrated in Table 6.
| Fraudulent | Legitimate | |
| Refuse | 20$ | -20$ |
| Approve | -100$ | 50$ |
These misclassification cost values can be given by domain experts, or can be learned via other approaches (Y. Sun, M.S. Kamel, A.K.C. Wong, Y. Wang, Cost-sensitive boosting for classification of imbalanced data, Pattern Recognition 40 (12) (2007) 3358–3378. doi: 10.1016/j.patcog.2007.04.009, Y. Sun, A.K.C. Wong, M.S. Kamel, Classification of imbalanced data: a review, International Journal of Pattern Recognition and Artificial Intelligence 23 (4) (2009) 687–719. doi: 10.1142/S0218001409007326). Specifically, when dealing with imbalanced problems, it is usually more interesting to recognize the positive instances rather than the negative ones. Therefore, the cost when misclassifying a positive instance must be higher than the cost of misclassifying a negative one, i.e. C(+,-) > C(-,+).
Given the cost matrix, an example should be classified into the class that has the lowest expected cost, which is known as the minimum expected cost principle. The expected cost R(i|x) of classifying an instance x into class i (by a classifier) can be expressed as:
$$R(i|x)=\sum_{j}P(j|x)·C(i,j)$$
where P(j|x) is the probability estimation of classifying an instance into class j. That is, the classifier will classify an instance x into positive class if and only if:
$$P(0|x)·C(1,0)+P(1|x)·C(1,1) \le P(0|x) · C(0,0)+P(1|x)·C(0,1)$$
or, which is equivalent:
$$P(0|x)·(C(1,0)-C(0,0)) \le P(1|x)(C(0,1)-C(1,1)$$
Therefore, any given cost-matrix can be converted to one with C(0,0) = C(1,1) = 0. Under this assumption, the classifier will classify an instance x into positive class if and only if:
$$P(0|x)·C(1,0) \le P(1|x)·C(0,1)$$
As P(0|x) = 1 - P(1|x), we can obtain a threshold p* for the classifier to classify an instance x into positive if P(1|x) > p*, where
$$p^*=\frac{C(1,0)}{C(1,0)-C(0,1)}=\frac{FP}{FP+FN}$$
Another possibility is to "rebalance" the original training examples the ratio of:
p(1)FN : p(0)FP
where p(1) and p(0) are the prior probability of the positive and negative examples in the original training set.
In summary, two main general approaches have been proposed to deal with cost-sensitive problems:
- Direct methods: The main idea of building a direct cost-sensitive learning algorithm is to directly introduce and utilize misclassification costs into the learning algorithms. For example, in the context of decision tree induction, the tree-building strategies are adapted to minimize the misclassification costs. The cost information is used to: (1) choose the best attribute to split the data (C.X. Ling, Q. Yang, J. Wang, S. Zhang, Decision trees with minimal costs, in: C.E. Brodley (Ed.), Proceedings of the 21st International Conference on Machine Learning (ICML’04), ACM International Conference Proceeding Series, vol. 69, ACM, 2004, pp. 69–77., P. Riddle, R. Segal, O. Etzioni, Representation design and brute-force induction in a boeing manufacturing domain, Applied Artificial Intelligence 8 (1994) 125–147. doi: 10.1080/08839519408945435); and (2) determine whether a subtree should be pruned (J.P. Bradford, C. Kunz, R. Kohavi, C. Brunk, C.E. Brodley, Pruning decision trees with misclassification costs, in: Proceedings of the 10th European Conference on Machine Learning (ECML’98), 1998, pp. 131–136.). On the other hand, other approaches based on genetic algorithms can incorporate misclassification costs in the fitness function (P.D. Turney, Cost-sensitive classification: empirical evaluation of a hybrid genetic decision tree induction algorithm, Journal of Artificial Intelligence Research 2 (1995) 369–409. doi: 10.1613/jair.120).
- Meta-learning: This methodology implies the integration of a "preprocessing" mechanism for the training data or a "postprocessing" of the output, in such a way that the original learning algorithm is not modified. Cost-sensitive meta-learning can be further classified into two main categories: thresholding and sampling, which are based on the two last expressions presented respectively:
- Thresholding is based on the basic decision theory that assigns instances to the class with minimum expected cost. For example, a typical decision tree for a binary classification problem assigns the class label of a leaf node depending on the majority class of the training samples that reach the node. A cost-sensitive algorithm assigns the class label to the node that minimizes the classification cost (P. Domingos, Metacost: a general method for making classifiers cost–sensitive, in: Proceedings of the 5th International Conference on Knowledge Discovery and Data Mining (KDD’99), 1999, pp. 155–164., B. Zadrozny, C. Elkan, Learning and making decisions when costs and probabilities are both unknown, in: Proceedings of the 7th International Conference on Knowledge Discovery and Data Mining (KDD’01), 2001, pp. 204–213.).
- Sampling is based on modifying the training dataset. The most popular technique lies in resampling the original class distribution of the training dataset according to the cost decision matrix by means of undersampling/oversampling (B. Zadrozny, J. Langford, N. Abe, Cost–sensitive learning by cost–proportionate example weighting, in: Proceedings of the 3rd IEEE International Conference on Data Mining (ICDM’03), 2003, pp. 435–442.) or assigning instance weights (K.M. Ting, An instance-weighting method to induce cost-sensitive trees, IEEE Transactions on Knowledge and Data Engineering 14 (3) (2002) 659–665. doi: 10.1109/TKDE.2002.1000348). These modifications have shown to be effective and can also be applied to any cost insensitive learning algorithm (Z.-H. Zhou, X.-Y. Liu, Training cost-sensitive neural networks with methods addressing the class imbalance problem, IEEE Transactions on Knowledge and Data Engineering 18 (1) (2006) 63–77. doi: 10.1109/TKDE.2006.17).
Ensemble Methods
Ensemble-based classifiers, also known as multiple classifier systems (R. Polikar, Ensemble based systems in decision making, IEEE Circuits and Systems Magazine 6 (3) (2006) 21–45. doi: 10.1109/MCAS.2006.1688199), try to improve the performance of single classifiers by inducing several classifiers and combining them to obtain a new classifier that outperforms every one of them. Hence, the basic idea is to construct several classifiers from the original data and then aggregate their predictions when unknown instances are presented.
In recent years, ensembles of classifiers have arisen as a possible solution to the class imbalance problem (L.I. Kuncheva, J.J. Rodrguez, A weighted voting framework for classifiers ensembles, Knowledge and Information Systems (2013), In press. doi: 10.1007/s10115-012-0586-6, X.-Y. Liu, J. Wu, Z.-H. Zhou, Exploratory undersampling for class-imbalance learning, IEEE Transactions on System, Man and Cybernetics B 39 (2) (2009) 539–550. doi: 10.1109/TSMCB.2008.2007853, C. Seiffert, T.M. Khoshgoftaar, J. Van Hulse, A. Napolitano, RUSBoost: a hybrid approach to alleviating class imbalance, IEEE Transactions on System, Man and Cybernetics A 40 (1) (2010) 185–197. doi: 10.1109/TSMCA.2009.2029559, Y. Sun, M.S. Kamel, A.K.C. Wong, Y. Wang, Cost-sensitive boosting for classification of imbalanced data, Pattern Recognition 40 (12) (2007) 3358–3378. doi: 10.1016/j.patcog.2007.04.009, J. Van Hulse, T.M. Khoshgoftaar, A. Napolitano, An empirical comparison of repetitive undersampling techniques, in: Proceedings of the 2009 IEEE International Conference on Information Reuse, Integration (IRI’09), 2009, pp. 29–34., S. Wang, X. Yao, Relationships between diversity of classification ensembles and single-class performance measures, IEEE Transactions on Knowledge and Data Engineering 25 (1) (2013) 206–219. doi: 10.1109/TKDE.2011.207). Ensemble-based methods are based on a combination between ensemble learning algorithms and one of the previously discussed techniques, namely data and algorithmic approaches, or cost-sensitive learning solutions. In the case of adding a data level approach to the ensemble learning algorithm, the new hybrid method usually preprocess the data before training each classifier. On the other hand, cost-sensitive ensembles, instead of modifying the base classifier in order to accept costs in the learning process, guide the cost minimization procedure via the ensemble learning algorithm. In this way, the modification of the base learner is avoided, but the major drawback, which is the costs definition, is still present.
A complete taxonomy for ensemble methods for learning with imbalanced classes can be found on a recent review (M. Galar, A. Fernández, E. Barrenechea, H. Bustince, F. Herrera, A review on ensembles for class imbalance problem: bagging, boosting and hybrid based approaches, IEEE Transactions on Systems, Man, and Cybernetics – part C: Applications and Reviews 42 (4) (2012) 463–484. doi: 10.1109/TSMCC.2011.2161285), which we summarize in Fig. 15. Mainly, the authors distinguish four different families among ensemble approaches for imbalanced learning. On the one hand, they identified cost-sensitive boosting approaches which are similar to cost-sensitive methods, but where the costs minimization procedure is guided by a boosting algorithm. On the other hand, they distinguish three more families which have a common feature: all of them consist on embedding a data preprocessing technique in an ensemble learning algorithm. They categorized these three families depending on the ensemble learning algorithm used, i.e. boosting, bagging and hybrid ensembles.

Figure 15. Galar et al.'s proposed taxonomy for ensembles to address class imbalance problem
From the study in (M. Galar, A. Fernández, E. Barrenechea, H. Bustince, F. Herrera, A review on ensembles for class imbalance problem: bagging, boosting and hybrid based approaches, IEEE Transactions on Systems, Man, and Cybernetics – part C: Applications and Reviews 42 (4) (2012) 463–484. doi: 10.1109/TSMCC.2011.2161285), the authors concluded that ensemble-based algorithms are worthwhile, improving the results obtained by using data preprocessing techniques and training a single classifier. They also highlighted the good performance of simple approaches such as RUSBoost (C. Seiffert, T.M. Khoshgoftaar, J. Van Hulse, A. Napolitano, RUSBoost: a hybrid approach to alleviating class imbalance, IEEE Transactions on System, Man and Cybernetics A 40 (1) (2010) 185–197. doi: 10.1109/TSMCA.2009.2029559) or UnderBagging (R. Barandela, R.M. Valdovinos, J.S. Sánchez, New applications of ensembles of classifiers, Pattern Analysis Applications 6 (3) (2003) 245–256. doi: 10.1007/s10044-003-0192-z), which despite of being simple approaches, achieve a higher performance than many other more complex algorithms.
Experimental results
Several authors, and especially (G.E.A.P.A. Batista, R.C. Prati, M.C. Monard, A study of the behaviour of several methods for balancing machine learning training data, SIGKDD Explorations 6 (1) (2004) 20–29. doi: 10.1145/1007730.1007735), have developed an ordering of the approaches to address learning with imbalanced datasets regarding a classification metric such as the Area Under the ROC Curve. In this section we present a complete study on the suitability of some recent proposals for preprocessing, cost-sensitive learning and ensemble-based methods, carrying out an intrafamily comparison for selecting the best performing approaches and then developing and inter-family analysis, with the aim of observing whether there are differences among them.
We have made use of three classifiers based on different paradigms:
- C4.5 Decision tree (J.R. Quinlan, C4.5: Programs for Machine Learning, Morgan Kauffman, 1993.): For C4.5, we have set a confidence level of 0.25, the minimum number of item-sets per leaf was set to 2 and pruning was used as well to obtain the final tree.
- Support vector machines (C. Cortes, V. Vapnik, Support vector networks, Machine Learning 20 (1995) 273–297. doi: 10.1007/BF00994018): For the SVM, we have chosen Polykernel reference functions, with an internal parameter of 1.0 for the exponent of each kernel function and a penalty parameter of the error term of 1.0.
- Instance based learning (kNN) (G.J. McLachlan, Discriminant Analysis and Statistical Pattern Recognition, John Wiley and Sons, 2004.): In this case, we have selected 1 neighbor for determining the output class, using the euclidean distance metric.
We have gathered 66 datasets, whose features are summarized in Table 7, namely the number of examples (#Ex.), number of attributes (#Atts.) and IR. Estimates of the performance were obtained by means of a 5-fold cross-validation. That is, we split the dataset into 5 folds, each one containing 20% of the patterns of the dataset. For each fold, the algorithm was trained with the examples contained in the remaining folds and then tested with the current fold. This value is set up with the aim of having enough positive class instances in the different folds, hence avoiding additional problems in the data distribution (J.G. Moreno-Torres, F. Herrera, A preliminary study on overlapping and data fracture in imbalanced domains by means of genetic programming-based feature extraction, in: Proceedings of the 10th International Conference on Intelligent Systems Design and Applications (ISDA’10), 2010, pp. 501–506., J.G. Moreno-Torres, T. Raeder, R. Aláiz-Rodríguez, N.V. Chawla, F. Herrera, A unifying view on dataset shift in classification, Pattern Recognition 45 (1) (2012) 521–530. doi: 10.1016/j.patcog.2011.06.019), especially for highly imbalanced datasets.
| Name | #Ex. | #Atts. | IR | Name | #Ex. | #Atts. | IR |
|---|---|---|---|---|---|---|---|
| Glass1 | 214 | 9 | 1.82 | Glass04vs5 | 92 | 9 | 9.22 |
| Ecoli0vs1 | 220 | 7 | 1.86 | Ecoli0346vs5 | 205 | 7 | 9.25 |
| Wisconsin | 683 | 9 | 1.86 | Ecoli0347vs56 | 257 | 7 | 9.28 |
| Pima | 768 | 8 | 1.90 | Yeast05679vs4 | 528 | 8 | 9.35 |
| Iris0 | 150 | 4 | 2.00 | Ecoli067vs5 | 220 | 6 | 10.00 |
| Glass0 | 214 | 9 | 2.06 | Vowel0 | 988 | 13 | 10.10 |
| Yeast1 | 1484 | 8 | 2.46 | Glass016vs2 | 192 | 9 | 10.29 |
| Vehicle1 | 846 | 18 | 2.52 | Glass2 | 214 | 9 | 10.39 |
| Vehicle2 | 846 | 18 | 2.52 | Ecoli0147vs2356 | 336 | 7 | 10.59 |
| Vehicle3 | 846 | 18 | 2.52 | Led7digit02456789vs1 | 443 | 7 | 10.97 |
| Haberman | 306 | 3 | 2.68 | Glass06vs5 | 108 | 9 | 11.00 |
| Glass0123vs456 | 214 | 9 | 3.19 | Ecoli01vs5 | 240 | 6 | 11.00 |
| Vehicle0 | 846 | 18 | 3.23 | Glass0146vs2 | 205 | 9 | 11.06 |
| Ecoli1 | 336 | 7 | 3.36 | Ecoli0147vs56 | 332 | 6 | 12.28 |
| New-thyroid2 | 215 | 5 | 4.92 | Cleveland0vs4 | 177 | 13 | 12.62 |
| New-thyroid1 | 215 | 5 | 5.14 | Ecoli0146vs5 | 280 | 6 | 13.00 |
| Ecoli2 | 336 | 7 | 5.46 | Ecoli4 | 336 | 7 | 13.84 |
| Segment0 | 2308 | 19 | 6.01 | Yeast1vs7 | 459 | 8 | 13.87 |
| Glass6 | 214 | 9 | 6.38 | Shuttle0vs4 | 1829 | 9 | 13.87 |
| Yeast3 | 1484 | 8 | 8.11 | Glass4 | 214 | 9 | 15.47 |
| Ecoli3 | 336 | 7 | 8.19 | Page-blocks13vs2 | 472 | 10 | 15.85 |
| Page-blocks0 | 5472 | 10 | 8.77 | Abalone9vs18 | 731 | 8 | 16.68 |
| Ecoli034vs5 | 200 | 7 | 9.00 | Glass016vs5 | 184 | 9 | 19.44 |
| Yeast2vs4 | 514 | 8 | 9.08 | Shuttle2vs4 | 129 | 9 | 20.50 |
| Ecoli067vs35 | 222 | 7 | 9.09 | Yeast1458vs7 | 693 | 8 | 22.10 |
| Ecoli0234vs5 | 202 | 7 | 9.10 | Glass5 | 214 | 9 | 22.81 |
| Glass015vs2 | 172 | 9 | 9.12 | Yeast2vs8 | 482 | 8 | 23.10 |
| Yeast0359vs78 | 506 | 8 | 9.12 | Yeast4 | 1484 | 8 | 28.41 |
| Yeast02579vs368 | 1004 | 8 | 9.14 | Yeast1289vs7 | 947 | 8 | 30.56 |
| Yeast0256vs3789 | 1004 | 8 | 9.14 | Yeast5 | 1484 | 8 | 32.78 |
| Ecoli046vs5 | 203 | 6 | 9.15 | Ecoli0137vs26 | 281 | 7 | 39.15 |
| Ecoli01vs235 | 244 | 7 | 9.17 | Yeast6 | 1484 | 8 | 39.15 |
| Ecoli0267vs35 | 224 | 7 | 9.18 | Abalone19 | 4174 | 8 | 128.87 |
We must point out that the dataset partitions employed in this paper are available for download at the KEEL dataset repository (J. Alcalá-Fdez, A. Fernández, J. Luengo, J. Derrac, S. García, L. Sánchez, F. Herrera, KEEL data–mining software tool: data set repository, integration of algorithms and experimental analysis framework, Journal of Multi-Valued Logic and Soft Computing 17 (2–3) (2011) 255–287.), so that any interested researcher can use the same data for comparison.
As pointed out above, result sheets are categorized regarding the taxonomy of the methods: preprocessing, cost-sensitive learning, and ensembles. For each category, average results using the AUC metric (A.P. Bradley, The use of the area under the roc curve in the evaluation of machine learning algorithms, Pattern Recognition 30 (7) (1997) 1145–1159. doi: 10.1016/S0031-3203(96)00142-2, J. Huang, C.X. Ling, Using AUC and accuracy in evaluating learning algorithms, IEEE Transactions on Knowledge and Data Engineering 17 (3) (2005) 299–310. doi: 10.1109/TKDE.2005.50) are provided:
Software, Algorithm Implementations and Dataset Repository
All algorithms selected for the experimental framework have been included into the KEEL software, under a specific module for classification with imbalanced datasets. Additionally, KEEL contains a complete dataset repository in which all the problems used in this, and other related journal papers, are available for download. In this way, any interested researcher can use the same data partitions for comparison.

|
Knowledge Extraction based on Evolutionary Learning (KEEL): KEEL is a software tool to assess evolutionary algorithms for Data Mining problems including regression, classification, clustering, pattern mining and so on. It contains a big collection of classical knowledge extraction algorithms, preprocessing techniques (instance selection, feature selection, discretization, imputation methods for missing values, etc.), Computational Intelligence based learning algorithms, including evolutionary rule learning algorithms based on different approaches (Pittsburgh, Michigan and IRL, ...), and hybrid models such as genetic fuzzy systems, evolutionary neural networks, etc. It allows us to perform a complete analysis of any learning model in comparison to existing ones, including a statistical test module for comparison. Moreover, KEEL has been designed with a double goal: research and educational. This software tool will be available as open source software this summer. For more information about this tool, please refer to the following publication: |
- J. Alcalá-Fdez, L. Sánchez, S. García, M.J. del Jesus, S. Ventura, J.M. Garrell, J. Otero, C. Romero, J. Bacardit, V.M. Rivas, J.C. Fernández, F. Herrera, KEEL: A Software Tool to Assess Evolutionary Algorithms for Data Mining Problems. Soft Computing, 13:3 (2009) 307-318. doi: 10.1007/s00500-008-0323-y

|
KEEL Dataset Repository (KEEL-dataset): KEEL-dataset repository is devoted to the datasets in KEEL format which can be used with the software and provides a detailed categorization of the considered datasets and a description of their characteristics. Tables for the datasets in each category have also been created. These categories include standard classification datasets, datasets with missing values, imbalanced datasets for classification, multi instance classification datasets, multi label classification datasets and so on. For more information about this repository, please refer to the following publication: |
- J. Alcalá-Fdez, A. Fernández, J. Luengo, J. Derrac, S. García, L. Sánchez, F. Herrera, KEEL Data-Mining Software Tool: Data Set Repository, Integration of Algorithms and Experimental Analysis Framework. Journal of Multiple-Valued Logic and Soft Computing 17:2-3 (2011) 255-287.

Literature review
The field of Classification with Imbalanced Datasets has experienced a flourishing growth in the last decades. Many interesting works have been developed under this area; not only new methods, but several survey papers, books and significant approaches for addressing the learning ability of classifiers in this scenario.
With this aim, we will first present a personal selection of papers of interest for the research community in classification with imbalanced data-sets. Then, we will enumerate the main contributions of our research group to the development of this topic.
Papers of interest: surveys and highlighted studies
Studying the specialized liteature, we may observe that there is a growing interest in the field of research for Classification with Imbalanced datasets, as it is shown in the Figure below. According with the former, in this section we have made a bibliography compilation regarding some significant papers we have considered regarding this topic.
| Published Elements per year for imbalanced classification (Queried on 05-02-2014)  |
Citations per year for imbalanced classification (Queried on 05-02-2014)  |
Surveys and reviews
N. Japkowicz and S. Stephen The Class Imbalance Problem: A Systematic Study.
Intelligent Data Analysis 6:5 (2002): 429-450. ref: http://dl.acm.org/citation.cfm?id=1293954
Abstract: In machine learning problems, differences in prior class probabilities -- or class imbalances -- have been reported to hinder the performance of some standard classifiers, such as decision trees. This paper presents a systematic study aimed at answering three different questions. First, we attempt to understand the nature of the class imbalance problem by establishing a relationship between concept complexity, size of the training set and class imbalance level. Second, we discuss several basic re-sampling or cost-modifying methods previously proposed to deal with the class imbalance problem and compare their effectiveness. The results obtained by such methods on artificial domains are linked to results in real-world domains. Finally, we investigate the assumption that the class imbalance problem does not only affect decision tree systems but also affects other classification systems such as Neural Networks and Support Vector Machines
H. He, E.A. Garcia, Learning from imbalanced data.
IEEE Transactions on Knowledge and Data Engineering 21:9 (2009) 1263–1284. doi: 10.1109/TKDE.2008.239
Abstract: With the continuous expansion of data availability in many large-scale, complex, and networked systems, such as surveillance, security, Internet, and finance, it becomes critical to advance the fundamental understanding of knowledge discovery and analysis from raw data to support decision-making processes. Although existing knowledge discovery and data engineering techniques have shown great success in many real-world applications, the problem of learning from imbalanced data (the imbalanced learning problem) is a relatively new challenge that has attracted growing attention from both academia and industry. The imbalanced learning problem is concerned with the performance of learning algorithms in the presence of underrepresented data and severe class distribution skews. Due to the inherent complex characteristics of imbalanced data sets, learning from such data requires new understandings, principles, algorithms, and tools to transform vast amounts of raw data efficiently into information and knowledge representation. In this paper, we provide a comprehensive review of the development of research in learning from imbalanced data. Our focus is to provide a critical review of the nature of the problem, the state-of-the-art technologies, and the current assessment metrics used to evaluate learning performance under the imbalanced learning scenario. Furthermore, in order to stimulate future research in this field, we also highlight the major opportunities and challenges, as well as potential important research directions for learning from imbalanced data.
Y. Sun, A.K.C. Wong, M.S. Kamel Classification of Imbalanced Data: a Review.
International Journal of Pattern Recognition and Artificial Intelligence 23:4 (2009) 687-719. doi: 10.1142/S0218001409007326
Abstract: Classification of data with imbalanced class distribution has encountered a significant drawback of the performance attainable by most standard classifier learning algorithms which assume a relatively balanced class distribution and equal misclassification costs. This paper provides a review of the classification of imbalanced data regarding: the application domains; the nature of the problem; the learning difficulties with standard classifier learning algorithms; the learning objectives and evaluation measures; the reported research solutions; and the class imbalance problem in the presence of multiple classes.
M. Galar, A. Fernández, E. Barrenechea, H. Bustince, F. Herrera, A review on ensembles for class imbalance problem: bagging, boosting and hybrid based approaches.
IEEE Transactions on Systems, Man, and Cybernetics – part C: Applications and Reviews 42:4 (2012) 463–484. doi: 10.1109/TSMCC.2011.2161285
Abstract: Classifier learning with data-sets suffering from imbalanced class distributions is a challenging problem in data mining community. This issue occurs when the number of examples representing one class is much lower than the ones of the other classes. Its presence in many real-world applications has brought along a growth of attention from researchers. In machine learning, ensemble of classifiers are known to increase the accuracy of single classifiers by combining several of them, but neither these learning techniques alone solve the class imbalance problem, to deal with this issue the ensemble learning algorithms have to be designed specifically.
In this paper, our aim is to review the state-of-the-art on ensemble techniques in the framework of imbalanced data-sets, focusing on two-class problems. We propose a taxonomy for ensemble-based methods to address class imbalance where each proposal can be categorized depending on the inner ensemble methodology in which it is based. In addition, we develop a thorough empirical comparison considering the most significant published approaches, within the families of the taxonomy proposed, to show whether any of them makes a difference.
This comparison has shown the good behavior of the simplest approaches which combine random undersampling techniques with Bagging or Boosting ensembles. Also, the positive synergy between sampling techniques and Bagging has stood out. Furthermore, our results show empirically that ensemble-based algorithms are worthwhile since they outperform the mere use of preprocessing techniques before learning the classifier, therefore justifying the increase of complexity by means of a significant enhancement of the results.
Highlighted papers
N.V. Chawla, K.W. Bowyer, L.O. Hall, W.P. Kegelmeyer, SMOTE: Synthetic minority over-sampling technique
(2002) Journal Of Artificial Intelligence Research, 16: pp 321-357. doi: 10.1016/S0031-3203(96)00142-2
Summary: SMOTE, the most used preprocessing technique for classification with imbalanced datasets is introduced in this paper. It creates synthetic instances for the minority class for balancing the distribution of the training set.
N.V. Chawla, N. Japkowicz, A. Kotcz, Editorial: special issue on learning from imbalanced data sets.
ACM SIGKDD Explorations Newsletter6:1 (2004) pp: 1-6. doi: 10.1145/1007730.1007735
Summary: This paper introduces the first special issue for the topic of classification with imbalanced data-sets, back in 2004.
G.M. Weiss, Mining with rarity: a unifying framework
ACM SIGKDD Explorations Newsletter 6:1 pp 7–19. doi: 10.1145/1007730.1007734
Summary: The problem of small-disjuncts in problems with imbalanced data-sets is first established.
G.E.A.P.A. Batista, R.C. Prati, M.C. Monard, A study of the behaviour of several methods for balancing machine learning training data
(2004) ACM SIGKDD Explorations Newsletter 6:1 pp: 20–29. doi: 10.1145/1007730.1007735
Summary: This paper is a mile-stone for the topic, as it presents a thorough experimental study for the most relevant preprocessing techniques in imbalanced learning.
H. Guo, H.L. Viktor, Learning from imbalanced data sets with boosting and data generation: the DataBoost-IM approach
(2004) ACM SIGKDD Explorations Newsletter 6:1 pp: 30–39. doi: 10.1145/1007730.1007736
Summary: In this work, authors introduced one of the pionneer ensemble methods for classification with imbalanced data.
T. Jo, N. Japkowicz, Class imbalances versus small disjuncts
ACM SIGKDD Explorations Newsletter 6:1 pp: 40–49. doi: 10.1145/1007730.1007737
Summary: In conjunction with the previous work by G.M. Weiss, this work introduces the problem of small disjuncts in imbalanced learning
A. Estabrooks, T.H. Jo, N. Japkowicz, A multiple resampling method for learning from imbalanced data sets
(2004) Computational Intelligence, 20:1 pp: 18-36. doi: 10.1111/j.0824-7935.2004.t01-1-00228.x
Summary: This paper presents an experimental study for contrasting preprocessing techniques, concluding that combining different expressions of the resampling approach is an effective solution to the tuning problem.
Y. Sun, M.S. Kamel, A.K.C. Wong, Y. Wang, Cost-sensitive boosting for classification of imbalanced data
(2007) Pattern Recognition, 40:12 pp: 3358-3378. doi: 10.1145/1007730.1007733
Summary: This paper proposes some ensemble learning mechanisms based in AdaBoost for cost-senstive learning.
N.V. Chawla, D.A. Cieslak, L.O. Hall, A. Joshi, Automatically countering imbalance and its empirical relationship to cost
(2008) Data Mining And Knowledge Discovery, 17:2 pp: 225-252. doi: 10.1007/s10618-008-0087-0
Summary: A wrapper preprocessing approach is proposed for determining the optimal degree of resampling that must be performed to a given dataset.
V. García, R.A. Mollineda, J.S. Sánchez, On the k-NN performance in a challenging scenario of imbalance and overlapping
(2008) Pattern Analysis Applications 11:3–4 pp: 269–280. doi:10.1007/s10044-007-0087-5
Summary: In this work, authors analyze the influence of overlapping for the learning ability of kNN classifiers in imbalanced classification, stressing that the main problem in this scenario is mainly the separability between the classes, rather than just the skewed distribution.
J. Van Hulse, T. Khoshgoftaar, Knowledge discovery from imbalanced and noisy data
(2009) Data & Knowledge Engineering, 68:12 pp: 1513-1542. doi: 10.1007/s10618-008-0087-0
Summary: Authors study in this paper the relationship between class imbalance and labeling errors, as they present significant challenges to data mining and knowledge discovery applications.
M. Wasikowski, X-W. Chen, Combating the Small Sample Class Imbalance Problem Using Feature Selection
(2010) IEEE Transactions On Knowledge And Data Engineering, 22:10 pp: 1388-1400. doi: 10.1109/TKDE.2009.187
Summary: This paper presents a first systematic comparison of the preprocessing methods for imbalanced data classification problems and of several feature selection metrics evaluated on small sample data sets from different applications.
C. Seiffert, T.M. Khoshgoftaar, J. Van Hulse, A. Napolitano, RUSBoost: A Hybrid Approach to Alleviating Class Imbalance
(2010) IEEE Transactions On Systems Man And Cybernetics Part A-Systems And Humans, 40:1 pp: 185-197. doi: 10.1109/TSMCA.2009.2029559
Summary: In this paper, authors present a new hybrid sampling/boosting algorithm, called RUSBoost, for learning from skewed training data. This algorithm provides a simpler and faster alternative to SMOTEBoost, which is another algorithm that combines boosting and data sampling.
SCI2S Related Approaches
S. Río, V. López, J.M. Benítez, F. Herrera, On the use of MapReduce for Imbalanced Big Data using Random Forest. Information Sciences, doi: 10.1016/j.ins.2014.03.043, in press (2014). ![]()
Abstract: In this age, big data applications are increasingly becoming the main focus of attention because of the enormous increment of data generation and storage that has taken place in the last years. This situation becomes a challenge when huge amounts of data are processed to extract knowledge because the data mining techniques are not adapted to the new space and time requirements. Furthermore, real-world data applications usually present a class distribution where the samples that belong to one class, which is precisely the main interest, are hugely outnumbered by the samples of the other classes. This circumstance, known as the class imbalance problem, complicates the learning process as the standard learning techniques do not correctly address this situation.
In this work, we analyse the performance of several techniques used to deal with imbalanced datasets in the big data scenario using the Random Forest classifier. Specifically, oversampling, undersampling and cost-sensitive learning have been adapted to big data using MapReduce so that these techniques are able to manage datasets as large as needed providing the necessary support to correctly identify the underrepresented class. The Random Forest classifier provides a solid basis for the comparison because of its performance, robustness and versatility.
An experimental study is carried out to evaluate the performance of the diverse algorithms considered. The results obtained show that there is not an approach to imbalanced big data classification that outperforms the others for all the data considered when using Random Forest. Moreover, even for the same type of problem, the best performing method is dependent on the number of mappers selected to run the experiments. In most of the cases, when the number of splits is increased, an improvement in the running times can be observed, however, this progress in times is obtained at the expense of a slight drop in the accuracy performance obtained. This decrement in the performance is related to the lack of density problem, which is evaluated in this work from the imbalanced data point of view, as this issue degrades the performance of classifiers in the imbalanced scenario more severely than in standard learning.
V. López, S. Río, J.M. Benítez, F. Herrera, Cost-Sensitive Linguistic Fuzzy Rule Based Classification Systems under the MapReduce Framework for Imbalanced Big Data. Fuzzy Sets and Systems, doi: 10.1016/j.fss.2014.01.015, in press (2014). ![]()
Abstract: Classification with big data has become one of the latest trends when talking about learning from the available information. The data growth in the last years has rocketed the interest in effectively acquiring knowledge to analyze and predict trends. The variety and veracity that are related to big data introduce a degree of uncertainty that has to be handled in addition to the vol- ume and velocity requirements. This data usually also presents what is known as the problem of classification with imbalanced datasets, a class distribution where the most important concepts to be learned are presented by a negligible number of examples in relation to the number of examples from the other classes. In order to adequately deal with imbalanced big data we propose the Chi-FRBCS-BigDataCS algorithm, a fuzzy rule based classification system that is able to deal with the uncertainly that is intro- duced in large volumes of data without disregarding the learning in the underrepresented class. The method uses the MapReduce framework to distribute the computational operations of the fuzzy model while it includes cost-sensitive learning techniques in its design to address the imbalance that is present in the data. The good performance of this approach is supported by the experimental analysis that is carried out over twenty-four imbalanced big data cases of study. The results obtained show that the proposal is able to handle these problems obtaining competitive results both in the classification performance of the model and the time needed for the computation
V. López, I. Triguero, C.J. Carmona, S. García, F. Herrera, Addressing Imbalanced Classification with Instance Generation Techniques: IPADE-ID. Neurocomputing 126 (2014) 15-28, doi: 10.1016/j.neucom.2013.01.050. ![]()
Abstract: A wide number of real word applications presents a class distribution where examples belonging to one class heavily outnumber the examples in the other class. This is an arduous situation where standard classification techniques usually decrease their performance, creating a handicap to correctly identify the minority class, which is precisely the case under consideration in these applications.
In this work, we propose the usage of the Iterative Instance Adjustment for Imbalanced Domains (IPADE-ID) algorithm. It is an evolutionary framework, which uses an instance generation technique, designed to face the existing imbalance modifying the original training set. The method, iteratively learns the appropriate number of examples that represent the classes and their particular positioning. The learning process contains three key operations in its design: a customized initialization procedure, an evolutionary optimization of the positioning of the examples and a selection of the most representative examples for each class.
An experimental analysis is carried out with a wide range of highly imbalanced datasets over the proposal and recognized solutions to the problem. The results obtained, which have been contrasted through non- parametric statistical tests, show that our proposal outperforms previously proposed methods.
V. López, A. Fernandez, F. Herrera, On the Importance of the Validation Technique for Classification with Imbalanced Datasets: Addressing Covariate Shift when Data is Skewed. Information Sciences 257 (2014) 1-13, doi: 10.1016/j.ins.2013.09.038. ![]()
Abstract: In the field of Data Mining, the estimation of the quality of the learned models is a key step in order to select the most appropriate tool for the problem to be solved. Traditionally, a k-fold validation technique has been carried out so that there is a certain degree of independency among the results for the different partitions. In this way, the highest average performance will be obtained by the most robust approach. However, applying a "random" division of the instances over the folds may result in a problem known as dataset shift, which consists in having a different data distribution between the training and test folds.
In classification with imbalanced datasets, in which the number of instances of one class is much lower than the other class, this problem is more severe. The misclassification of minority class instances due to an incorrect learning of the real boundaries caused by a not well fitted data distribution, truly affects the measures of performance in this scenario. Regarding this fact, we propose the use of a specific validation technique for the partitioning of the data, known as "Distribution optimally balanced stratified cross-validation" to avoid this harmful situation in the presence of imbalance. This methodology makes the decision of placing close-by samples on different folds, so that each partition will end up with enough representatives of every region.
We have selected a wide number of imbalanced datasets from KEEL dataset repository for our study, using several learning techniques from different paradigms, thus making the conclusions extracted to be independent of the underlying classifier. The analysis of the results has been carried out by means of the proper statistical study, which shows the goodness of this approach for dealing with imbalanced data.
V. López, A. Fernandez, S. García, V. Palade, F. Herrera, An Insight into Classification with Imbalanced Data: Empirical Results and Current Trends on Using Data Intrinsic Characteristics. Information Sciences 250 (2013) 113-141, doi: 10.1016/j.ins.2013.07.007. ![]()
Abstract: Training classifiers with datasets which suffer of imbalanced class distributions is an important problem in data mining. This issue occurs when the number of examples representing the class of interest is much lower than the ones of the other classes. Its presence in many real-world applications has brought along a growth of attention from researchers.
We shortly review the many issues in machine learning and applications of this problem, by introducing the characteristics of the imbalanced dataset scenario in classification, presenting the specific metrics for evaluating performance in class imbalanced learning and enumerating the proposed solutions. In particular, we will describe preprocessing, cost-sensitive learning and ensemble techniques, carrying out an experimental study to contrast these approaches in an intra and inter-family comparison.
We will carry out a thorough discussion on the main issues related to using data intrinsic characteristics in this classification problem. This will help to improve the current models with respect to: the presence of small disjuncts, the lack of density in the training data, the overlapping between classes, the identification of noisy data, the significance of the borderline instances, and the dataset shift between the training and the test distributions. Finally, we introduce several approaches and recommendations to address these problems in conjunction with imbalanced data, and we will show some experimental examples on the behavior of the learning algorithms on data with such intrinsic characteristics
M. Galar, A. Fernandez, E. Barrenechea, F. Herrera, EUSBoost: Enhancing Ensembles for Highly Imbalanced Data-sets by Evolutionary Undersampling. Pattern Recognition 46:12 (2013) 3460–3471, doi: j.patcog.2013.05.006. ![]()
Abstract: Classification with imbalanced data-sets has become one of the most challenging problems in Data Mining. Being one class much more represented than the other produces undesirable effects in both the learning and classification processes, mainly regarding the minority class. Such a problem needs accurate tools to be undertaken; lately, ensembles of classifi ers have emerged as a possible solution. Among ensemble proposals, the combination of Bagging and Boosting with preprocessing techniques has proved its ability to enhance the classification of the minority class.
In this paper, we develop a new ensemble construction algorithm (EUSBoost) based on RUSBoost, one of the simplest and most accurate ensemble, which combines random undersampling with Boosting algorithm. Our methodology aims to improve the existing proposals enhancing the performance of the base classifiers by the usage of the evolutionary undersampling approach. Besides, we promote diversity favoring the usage of different subsets of majority class instances to train each base classifier. Centered on two-class highly imbalanced problems, we will prove, supported by the proper statistical analysis, that EUSBoost is able to outperform the state-of-the-art methods based on ensembles. We will also analyze its advantages using kappa-error diagrams, which we adapt to the imbalanced scenario
V. López, A. Fernandez, M.J. del Jesus, F. Herrera, A Hierarchical Genetic Fuzzy System Based On Genetic Programming for Addressing Classification with Highly Imbalanced and Borderline Data-sets. Knowledge-Based Systems 38 (2013) 85-104, doi: 10.1016/j.knosys.2012.08.025. ![]()
Abstract: Lots of real world applications appear to be a matter of classification with imbalanced data-sets. This problem arises when the number of instances from one class is quite different to the number of instances from the other class. Traditionally, classification algorithms are unable to correctly deal with this issue as they are biased towards the majority class. Therefore, algorithms tend to misclassify the minority class which usually is the most interesting one for the application that is being sorted out.
Among the available learning approaches, fuzzy rule-based classification systems have obtained a good behavior in the scenario of imbalanced data-sets. In this work, we focus on some modifications to further improve the performance of these systems considering the usage of information granulation. Specifically, a positive synergy between data sampling methods and algorithmic modifications is proposed, creating a genetic programming approach that uses linguistic variables in a hierarchical way. These linguistic variables are adapted to the context of the problem with a genetic process that combines rule selection with the adjustment of the lateral position of the labels based on the 2-tuples linguistic model.
An experimental study is carried out over highly imbalanced and borderline imbalanced data-sets which is completed by a statistical comparative analysis. The results obtained show that the proposed model outperforms several fuzzy rule based classification systems, including a hierarchical approach and presents a better behavior than the C4.5 decision tree
A. Fernandez, V. López, M. Galar, M.J. del Jesus, F. Herrera, Analysing the Classification of Imbalanced Data-sets with Multiple Classes: Binarization Techniques and Ad-Hoc Approaches. Knowledge-Based Systems 42 (2013) 97-110, doi: 10.1016/j.knosys.2013.01.018. ![]()
Abstract: The imbalanced class problem is related to the real-world application of classification in engineering. It is characterised by a very different distribution of examples among the classes. The condition of multiple imbalanced classes is more restrictive when the aim of the final system is to obtain the most accurate precision for each of the concepts of the problem.
The goal of this work is to provide a thorough experimental analysis that will allow us to determine the behaviour of the different approaches proposed in the specialised literature. First, we will make use of binarization schemes, i.e., one versus one and one versus all, in order to apply the standard approaches to solving binary class imbalanced problems. Second, we will apply several ad hoc procedures which have been designed for the scenario of imbalanced data-sets with multiple classes.
This experimental study will include several well-known algorithms from the literature such as decision trees, support vector machines and instance-based learning, with the intention of obtaining global conclusions from different classification paradigms. The extracted findings will be supported by a statistical comparative analysis using more than 20 data-sets from the KEEL repository
E. Ramentol, Y. Caballero, R. Bello, F. Herrera, SMOTE-RSB*: A Hybrid Preprocessing Approach based on Oversampling and Undersampling for High Imbalanced Data-Sets using SMOTE and Rough Sets Theory. Knowledge and Information Systems 33:2 (2012) 245-265, doi: 10.1007/s10115-011-0465-6. ![]()
Abstract: Imbalanced data is a common problem in classification. This phenomenon is growing in importance since it appears in most real domains. It has special relevance to highly imbalanced data-sets (when the ratio between classes is high). Many techniques have been developed to tackle the problem of imbalanced training sets in supervised learning. Such techniques have been divided into two large groups: those at the algorithm level and those at the data level. Data level groups that have been emphasized are those that try to balance the training sets by reducing the larger class through the elimination of samples or increasing the smaller one by constructing new samples, known as undersampling and oversampling, respectively. This paper proposes a new hybrid method for preprocessing imbalanced data-sets through the construction of new samples, using the Synthetic Minority Oversampling Technique together with the application of an editing technique based on the Rough Set Theory and the lower approximation of a subset. The proposed method has been validated by an experimental study showing good results using C4.5 as the learning algorithm.
A. Palacios, L. Sanchez, I. Couso, Combining Adaboost with preprocessing algorithms for extracting fuzzy rules from low quality data in possibly imbalanced datasets. International Journal of Uncertainty Fuzzines and Knowledge-based Systems 20:2 (2012) 51-71, doi: 10.1142/S0218488512400156. ![]()
Abstract: An extension of the Adaboost algorithm for obtaining fuzzy rule-based systems from low quality data is combined with preprocessing algorithms for equalizing imbalanced datasets. With the help of synthetic and real-world problems, it is shown that the performance of the Adaboost algorithm is degraded in presence of a moderate uncertainty in either the input or the output values. It is also establish ed that a preprocessing stage improves the accuracy of the classifier in a wide range of binary classification problems, including those whose imbalance ratio is uncertain.
V. López, A. Fernandez, J. G. Moreno-Torres, F. Herrera, Analysis of preprocessing vs. cost-sensitive learning for imbalanced classification. Open problems on intrinsic data characteristics. Expert Systems with Applications 39:7 (2012) 6585-6608, doi: 10.1016/j.eswa.2011.12.043. ![]()
Abstract: Class imbalance is among the most persistent complications which may confront the traditional supervised learning task in real-world applications. The problem occurs, in the binary case, when the number of instances in one class significantly outnumbers the number of instances in the other class. This situation is a handicap when trying to identify the minority class, as the learning algorithms are not usually adapted to such characteristics.
The approaches to deal with the problem of imbalanced datasets fall into two major categories: data sampling and algorithmic modification. Cost-sensitive learning solutions incorporating both the data and algorithm level approaches assume higher misclassification costs with samples in the minority class and seek to minimize high cost errors. Nevertheless, there is not a full exhaustive comparison between those models which can help us to determine the most appropriate one under different scenarios.
The main objective of this work is to analyze the performance of data level proposals against algorithm level proposals focusing in cost-sensitive models and versus a hybrid procedure that combines those two approaches. We will show, by means of a statistical comparative analysis, that we cannot highlight an unique approach among the rest. This will lead to a discussion about the data intrinsic characteristics of the imbalanced classification problem which will help to follow new paths that can lead to the improvement of current models mainly focusing on class overlap and dataset shift in imbalanced classification
P. Villar, A. Fernandez, R.A. Carrasco, F. Herrera, Feature Selection and Granularity Learning in Genetic Fuzzy Rule-Based Classification Systems for Highly Imbalanced Data-Sets. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems 20:3 (2012) 369-397, doi: S0218488512500195. ![]()
Abstract: This paper proposes a Genetic Algorithm for jointly performing a feature selection and granularity learning for Fuzzy Rule-Based Classification Systems in the scenario of highly imbalanced data-sets. We refer to imbalanced data-sets when the class distribution is not uniform, a situation that it is present in many real application areas. The aim of this work is to get more compact models by selecting the adequate variables and adapting the number of fuzzy labels for each problem, improving the interpretability of the model. The experimental analysis is carried out over a wide range of highly imbalanced data-sets and uses the statistical tests suggested in the specialized literature
S. García, J. Derrac, I. Triguero, C.J. Carmona, F. Herrera, Evolutionary-Based Selection of Generalized Instances for Imbalanced Classification. Knowledge Based Systems 25:1 (2012) 3-12 doi: 10.1016/j.knosys.2011.01.012. ![]()
Abstract: In supervised classification, we often encounter many real world problems in which the data do not have an equitable distribution among the different classes of the problem. In such cases, we are dealing with the so-called imbalanced data sets. One of the most used techniques to deal with this problem consists of preprocessing the data previously to the learning process. This paper proposes a method belonging to the family of the nested generalized exemplar that accomplishes learning by storing objects in Euclidean n-space. Classification of new data is performed by computing their distance to the nearest generalized exemplar. The method is optimized by the selection of the most suitable generalized exemplars based on evolutionary algorithms. An experimental analysis is carried out over a wide range of highly imbalanced data sets and uses the statistical tests suggested in the specialized literature. The results obtained show that our evolutionary proposal outperforms other classic and recent models in accuracy and requires to store a lower number of generalized examples
A. Palacios, L. Sanchez, I. Couso, Equalizing imbalanced imprecise datasets for genetic fuzzy classifiers. International Journal of Computational Intelligence Systems 5:2 (2012) 276-296 doi: 10.1080/18756891.2012.685292. ![]() .
.
Abstract: Determining whether an imprecise dataset is imbalanced is not immediate. The vagueness in the data causes that the prior probabilities of the classes are not precisely known, and therefore the degree of imbalance can also be uncertain. In this paper we propose suitable extensions of different resampling algorithms that can be applied to interval valued, multi-labelled data. By means of these extended preprocessing algorithms, certain classification systems designed for minimizing the fraction of misclassifications are able to produce knowledge bases that are also adequate under common metrics for imbalanced classification
J. Luengo, A. Fernandez, S. García, F. Herrera, Addressing Data Complexity for Imbalanced Data Sets: Analysis of SMOTE-based Oversampling and Evolutionary Undersampling. Soft Computing, 15 (10) (2011) 1909-1936 doi:10.1007/s00500-010-0625-8. ![]()
Abstract: In the classification framework there are problems in which the number of examples per class is not equitably distributed, formerly known as imbalanced data sets. This situation is a handicap when trying to identify the minority classes, as the learning algorithms are not usually adapted to such characteristics. An usual approach to deal with the problem of imbalanced data sets is the use of a preprocessing step. In this paper we analyze the usefulness of the data complexity measures in order to evaluate the behavior of undersampling and oversampling methods. Two classical learning methods, C4.5 and PART, are considered over a wide range of imbalanced data sets built from real data. Specifically, oversampling techniques and an evolutionary undersampling one have been selected for the study. We extract behavior patterns from the results in the data complexity space defined by the measures, coding them as intervals. Then, we derive rules from the intervals that describe both good or bad behaviors of C4.5 and PART for the different preprocessing approaches, thus obtaining a complete characterization of the data sets and the differences between the oversampling and undersampling results.
A. Fernandez, M.J. del Jesus, F. Herrera, On the 2-Tuples Based Genetic Tuning Performance for Fuzzy Rule Based Classification Systems in Imbalanced Data-Sets. Information Sciences 180:8 (2010) 1268-1291, doi:10.1016/j.ins.2009.12.014. COMPLEMENTARY MATERIAL to the paper here: dataset partitions, results, figures, etc.. ![]()
Abstract: When performing a classification task, we may find some data-sets with a different class distribution among their patterns. This problem is known as classification with imbalanced data-sets and it appears in many real application areas. For this reason, it has recently become a relevant topic in the area of Machine Learning.
The aim of this work is to improve the behaviour of fuzzy rule based classification systems (FRBCSs) in the framework of imbalanced data-sets by means of a tuning step. Specifically, we adapt the 2-tuples based genetic tuning approach to classification problems showing the good synergy between this method and some FRBCSs.
Our empirical results show that the 2-tuples based genetic tuning increases the performance of FRBCSs in all types of imbalanced data. Furthermore, when the initial Rule Base, built by a fuzzy rule learning methodology, obtains a good behaviour in terms of accuracy, we achieve a higher improvement in performance for the whole model when applying the genetic 2-tuples post-processing step. This enhancement is also obtained in the case of cooperation with a preprocessing stage, proving the necessity of rebalancing the training set before the learning phase when dealing with imbalanced data
S. García, F. Herrera Evolutionary Under-Sampling for Classification with Imbalanced Data Sets: Proposals and Taxonomy.
Evolutionary Computation 17:3 (2009) 275-306 doi: 10.1162/evco.2009.17.3.275 ![]()
Abstract: Learning with imbalanced data is one of the recent challenges in machine learning. Various solutions have been proposed in order to find a treatment for this problem, such as modifying methods or the application of a preprocessing stage. Within the preprocessing focused on balancing data, two tendencies exist: reduce the set of examples (undersampling) or replicate minority class examples (oversampling). Undersampling with imbalanced datasets could be considered as a prototype selection procedure with the purpose of balancing datasets to achieve a high classification rate, avoiding the bias toward majority class examples. Evolutionary algorithms have been used for classical prototype selection showing good results, where the fitness function is associated to the classification and reduction rates. In this paper, we propose a set of methods called evolutionary undersampling that take into consideration the nature of the problem and use different fitness functions for getting a good trade-off between balance of distribution of classes and performance. The study includes a taxonomy of the approaches and an overall comparison among our models and state of the art undersampling methods. The results have been contrasted by using nonparametric statistical procedures and show that evolutionary undersampling outperforms the nonevolutionary models when the degree of imbalance is increased.
A. Fernandez, F. Herrera, M.J. del Jesus, On the Influence of an Adaptive Inference System in Fuzzy Rule Based Classification Systems for Imbalanced Data-Sets. Expert Systems With Applications 36:6 (2009) 9805-9812, doi: 10.1016/j.eswa.2009.02.048. ![]()
Abstract: Classification with imbalanced data-sets supposes a new challenge for researches in the framework of data mining. This problem appears when the number of examples that represents one of the classes of the data-set (usually the concept of interest) is much lower than that of the other classes. In this manner, the learning model must be adapted to this situation, which is very common in real applications.
In this paper, we will work with fuzzy rule based classification systems using a preprocessing step in order to deal with the class imbalance. Our aim is to analyze the behaviour of fuzzy rule based classifi- cation systems in the framework of imbalanced data-sets by means of the application of an adaptive inference system with parametric conjunction operators.
Our results shows empirically that the use of the this parametric conjunction operators implies a higher performance for all data-sets with different imbalanced ratios
S. García, A. Fernandez, F. Herrera, Enhancing the Effectiveness and Interpretability of Decision Tree and Rule Induction Classifiers with Evolutionary Training Set Selection over Imbalanced Problems. Applied Soft Computing 9 (2009) 1304-1314, doi:10.1016/j.asoc.2009.04.004. ![]()
Abstract: Classification in imbalanced domains is a recent challenge in data mining. We refer to imbalanced classification when data presents many examples from one class and few from the other class, and the less representative class is the one which has more interest from the point of view of the learning task. One of the most used techniques to tackle this problem consists in preprocessing the data previously to the learning process. This preprocessing could be done through under-sampling; removing examples, mainly belonging to the majority class; and over-sampling, by means of replicating or generating new minority examples. In this paper, we propose an under-sampling procedure guided by evolutionary algorithms to perform a training set selection for enhancing the decision trees obtained by the C4.5 algorithm and the rule sets obtained by PART rule induction algorithm. The proposal has been compared with other under-sampling and over-sampling techniques and the results indicate that the new approach is very competitive in terms of accuracy when comparing with over-sampling and it outperforms standard under-sampling. Moreover, the obtained models are smaller in terms of number of leaves or rules generated and they can considered more interpretable. The results have been contrasted through non-parametric statistical tests over multiple data sets.
A. Fernandez, M.J. del Jesus, F. Herrera, Hierarchical Fuzzy Rule Based Classification Systems with Genetic Rule Selection for Imbalanced Data-Sets. International Journal of Approximate Reasoning 50 (2009) 561-577, doi: 10.1016/j.ijar.2008.11.004. COMPLEMENTARY MATERIAL to the paper here: dataset partitions, results, figures, etc.. ![]()
Abstract: In many real application areas, the data used are highly skewed and the number of instances for some classes are much higher than that of the other classes. Solving a classification task using such an imbalanced data-set is difficult due to the bias of the training towards the majority classes.
The aim of this paper is to improve the performance of fuzzy rule based classification systems on imbalanced domains, increasing the granularity of the fuzzy partitions on the boundary areas between the classes, in order to obtain a better separability. We propose the use of a hierarchical fuzzy rule based classification system, which is based on the refinement of a simple linguistic fuzzy model by means of the extension of the structure of the knowledge base in a hierarchical way and the use of a genetic rule selection process in order to get a compact and accurate model.
The good performance of this approach is shown through an extensive experimental study carried out over a large collection of imbalanced data-sets.
A. Fernandez, S. García, M.J. del Jesus, F. Herrera, A Study of the Behaviour of Linguistic Fuzzy Rule Based Classification Systems in the Framework of Imbalanced Data Sets. Fuzzy Sets and Systems, 159:18 (2008) 2378-2398, doi: 10.1016/j.fss.2007.12.023. ![]()
Abstract: In the field of classification problems, we often encounter classes with a very different percentage of patterns between them, classes with a high pattern percentage and classes with a low pattern percentage. These problems receive the name of "classification problems with imbalanced data-sets". In this paper we study the behaviour of fuzzy rule based classification systems in the framework of imbalanced data-sets, focusing on the synergy with the preprocessing mechanisms of instances and the configuration of fuzzy rule based classification systems. We will analyse the necessity of applying a preprocessing step to deal with the problem of imbalanced data-sets. Regarding the components of the fuzzy rule base classification system, we are interested in the granularity of the fuzzy partitions, the use of distinct conjunction operators, the application of some approaches to compute the rule weights and the use of different fuzzy reasoning methods.
