h-index and Variants
This Website contains additional material to the SCI2S research paper on "h-index and review" 
S. Alonso, F.J. Cabrerizo, E. Herrera-Viedma, F. Herrera, h-index: A Review Focused in its Variants, Computation and Standardization for Different Scientific Fields. Journal of Informetrics 3:4 (2009) 273-289, doi:10.1016/j.joi.2009.04.001. ![]()
The web is organized according to the following summary:
- h-index: definition, applications, advantages and disadvantages
- New indices based on h-index
- Standarization of the h-index for comparing scientific that work in different scientific fields
- Some studies analyzing the indices
- Studies comparing h-index and other bibliometric indicators
- Studies that analyze h- based indices and their correlations
- Studies about how self-citation affect the h-index
- Studies that stablish some axioms and mathematical interpretations of h- based indices
- Other studies that analyze the performance of different indices and their transformations
- How to compute h-index using different Databases?
- On the use of h- related indices to assess groups of individuals, institutions and journals
- Empirical studies that use h- and related indices
- WEB sites or journal special issues devoted to h-index
- Bibliography compilation about the h-index and related areas
h-index: definition, applications, advantages and disadvantages
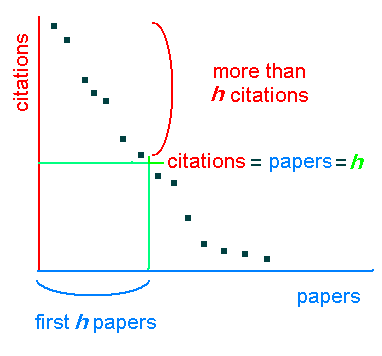
Definition: (Hirsch JE (2005) An index to quantify an individual's scientific research output. Proceedings of the National Academy of Sciences 102:16569-16572, doi: 10.1073/pnas.0507655102 ![]() ) A scientist has index h if h of his or her Np papers have at least h citations each and the other (Np - h) papers have ≤ h citations each.
) A scientist has index h if h of his or her Np papers have at least h citations each and the other (Np - h) papers have ≤ h citations each.
Applications: Hirsch originally suggested the h-index for application at the micro level, that is, as a measure to quantify the scientific output of a single researcher. However, the h-index can be used not only for the lifetime achievements of a single researcher but can be applied to any (more extensive) publication set (Rousseau R (2006) New developments related to the Hirsch index. Industrial Sciences and Technology, Belgium, . ![]() ).
).
- Van Raan (Van Raan AFJ (2006) Comparison of the Hirsch-index with standard bibliometric indicators and with peer judgment for 147 chemistry research groups. Scientometrics 67(3):491-502, doi: 10.1007/s11192-006-0066-4 .
 ) calculates the h-index for university research groups in chemistry and chemical engineering in the Netherlands. With calculation of the h-index for individual research groups, van Raan is applying the index for quantification of scientific performance no longer at the micro but at the meso level.
) calculates the h-index for university research groups in chemistry and chemical engineering in the Netherlands. With calculation of the h-index for individual research groups, van Raan is applying the index for quantification of scientific performance no longer at the micro but at the meso level. - Braun, Glanzel and Schubert (Braun T, Glänzel W, Schubert A (2006) A Hirsch-type index for journals. Scientometrics 69(1):169-173, doi: 10.1007/s11192-006-0147-4 .
 ) propose a Hirsch-type index for evaluating the scientific impact of journals as a robust alternative indicator that is an advantageous complement to journal impact factors.
) propose a Hirsch-type index for evaluating the scientific impact of journals as a robust alternative indicator that is an advantageous complement to journal impact factors. - Banks (Banks MG (2006) An extension of the Hirsch index: Indexing scientific topics and compounds. Scientometrics 69(1):161-168, doi: 10.1007/s11192-006-0146-5 .
 ) applies the h-index to the case of interesting topics and compounds: Bank's h - b index is found by entering a topic (search string, like "superstring" or "teleportation") or compound (name or chemical formula) into the Web of Science database and then ordering the results in terms of citations, by largest first. The h - b is then defined in the same manner as the h-index. With calculation of the h - b index, it can be determined how much work has already been done on certain topics or compounds, what the "hot topics" (or "older topics") of interest are, or what topic or compound is mainstream research at the present time.
) applies the h-index to the case of interesting topics and compounds: Bank's h - b index is found by entering a topic (search string, like "superstring" or "teleportation") or compound (name or chemical formula) into the Web of Science database and then ordering the results in terms of citations, by largest first. The h - b is then defined in the same manner as the h-index. With calculation of the h - b index, it can be determined how much work has already been done on certain topics or compounds, what the "hot topics" (or "older topics") of interest are, or what topic or compound is mainstream research at the present time.
Advantages: (Costas R, Bordons M (2007) Advantages, limitations and its relation with other bibliometric indacators at the micro level. Journal of Informetrics 1(3):193-203, doi: 10.1016/j.joi.2007.02.001 . ![]() )
)
- It combines a measure of quantity (publications) and impact (citations).
- It allows us to characterize the scientific output of a researcher with objectivity and, therefore, may play an important role when making decisions about promotions, fund allocation and awarding prizes.
- It performs better than other single-number criteria commonly used to evaluate the scientific output of a researcher (impact factor, total number of documents, total number of citations, citation per paper rate and number of highly cited papers).
- The h-index can be easily obtained by anyone with access to the Thomson ISI Web of Science and, in addition, it is easy to understand.
Disadvantages: (Costas R, Bordons M (2007) Advantages, limitations and its relation with other bibliometric indacators at the micro level. Journal of Informetrics 1(3):193-203, doi: 10.1016/j.joi.2007.02.001 . ![]() )
)
- There are inter-field differences in typical h values due to differences among fields in productivity and citation practices (Hirsch JE (2005) An index to quantify an individual's scientific research output. Proceedings of the National Academy of Sciences 102:16569-16572, doi: 10.1073/pnas.0507655102 .
 ), so the h-index should not be used to compare scientists from different disciplines.
), so the h-index should not be used to compare scientists from different disciplines. - The h-index depends on the duration of each scientist's career because the pool of publications and citations increases over time (Hirsch JE (2005) An index to quantify an individual's scientific research output. Proceedings of the National Academy of Sciences 102:16569-16572, doi: 10.1073/pnas.0507655102 .
 ; Kelly CD, Jennions MD (2006) The h-index and career assessment by numbers. Trends in Ecology and Evolution 21(4):167-170, doi: 10.1016/j.tree.2006.01.005 .
; Kelly CD, Jennions MD (2006) The h-index and career assessment by numbers. Trends in Ecology and Evolution 21(4):167-170, doi: 10.1016/j.tree.2006.01.005 .  ). In order to compare scientists at different stages of their career, Hirsch (Hirsch JE (2005) An index to quantify an individual's scientific research output. Proceedings of the National Academy of Sciences 102:16569-16572, doi: 10.1073/pnas.0507655102 .
). In order to compare scientists at different stages of their career, Hirsch (Hirsch JE (2005) An index to quantify an individual's scientific research output. Proceedings of the National Academy of Sciences 102:16569-16572, doi: 10.1073/pnas.0507655102 .  ) presented the "m parameter", which is the result of dividing h by the scientific age of a scientist (number of years since the author's first publication).
) presented the "m parameter", which is the result of dividing h by the scientific age of a scientist (number of years since the author's first publication). - Highly cited papers are important for the determination of the h-index, but once they are selected to belong to the top h papers, it is unimportant the number of citations they receive. This is a disadvantage of the h-index which Egghe has tried to overcome through a new index, called g-index (Egghe L (2006) Theory and practice of the g-index. Scientometrics 69(1):131-152, doi: 10.1007/s11192-006-0144-7 .
 ).
). - Since the h-index is easy to obtain, we run the risk of indiscriminate use, such as relying only on it for the assessment of scientists. Research performance is a complex multifaceted endeavour that cannot be assessed adequately by means of a single indicator:
- Martin BR (1996) The use of multiple indicators in the assessment of basic research. Scientometrics 36(3):343-362, doi: 10.1007/BF02129599 .

- Carbo-Dorca R. A monodimensional scientific performance measure: the h index, can be substituted by simple multidimensional descriptors?. Journal of the Mathematical Chemistry 47 (1) (2010) 548-550, doi: 10.1007/s10910-009-9573-x
- Yin C.Y., Aris M.J., Chen X. Combination of Eigenfactor (TM) and h-index to evaluate scientific journals. Scientometrics 84 (3) (2010) 639-648, doi: 10.1007/s11192-009-0116-9
- Martin BR (1996) The use of multiple indicators in the assessment of basic research. Scientometrics 36(3):343-362, doi: 10.1007/BF02129599 .
- The use of the h-index could provoke changes in the publishing behaviour of scientists, such an artificial increase in the number of self-citations distributed among the documents on the edge of the h-index (Van Raan AFJ (2006) Comparison of the Hirsch-index with standard bibliometric indicators and with peer judgment for 147 chemistry research groups. Scientometrics 67(3):491-502, doi: 10.1007/s11192-006-0066-4 .
 ).
). - There are also technical limitations, such as the difficulty to obtain the complete output of scientists with very common names, or whether selt-citations should be removed or not. Self-citations can increase a scientist's h, but their effect on h is much smaller than on the total citation count since only self-citations with a number of citations just > h are relevant (Hirsch JE (2005) An index to quantify an individual's scientific research output. Proceedings of the National Academy of Sciences 102:16569-16572, doi: 10.1073/pnas.0507655102 .
 ).
).
New indices based on h-index
Early indices based on the h-index
g-index: (Egghe L (2006) Theory and practise of the g-index. Scientometrics 69(1):131-152, doi: 10.1007/s11192-006-0144-7 . ![]() ) Holding that "a measure which should indicate the overall quality of a scientist ... should deal with the performance of the top articles," Egghe proposed the g-index as a modification of the h-index. For the calculation of the g-index, the same ranking of a publication set -paper in decreasing order of the number of citations received- is used as for the h-index. Egghe defines the g-index "as the highest number g of papers that together received g2 or more citations. From this definition it is already clear that g = h". In contrast to the h-index, the g-index gives more weight to highly cited papers. The aim is to avoid a disadvantage of the h-index that "once a paper belongs to the top h papers, its subsequent citations no longer 'count'" (Bornmann L, Mutz R, Daniel HD (2008) Are there better indices for evaluation purposes than the h index? A comparison of nine different variants of the h index using data from biomedicine. Journal of the American Society for Information Science and Technology 59(5):830-837, doi: 10.1002/asi.20806 .
) Holding that "a measure which should indicate the overall quality of a scientist ... should deal with the performance of the top articles," Egghe proposed the g-index as a modification of the h-index. For the calculation of the g-index, the same ranking of a publication set -paper in decreasing order of the number of citations received- is used as for the h-index. Egghe defines the g-index "as the highest number g of papers that together received g2 or more citations. From this definition it is already clear that g = h". In contrast to the h-index, the g-index gives more weight to highly cited papers. The aim is to avoid a disadvantage of the h-index that "once a paper belongs to the top h papers, its subsequent citations no longer 'count'" (Bornmann L, Mutz R, Daniel HD (2008) Are there better indices for evaluation purposes than the h index? A comparison of nine different variants of the h index using data from biomedicine. Journal of the American Society for Information Science and Technology 59(5):830-837, doi: 10.1002/asi.20806 . ![]() ).
).
a-index: (Jin BH, Liang LM, Rousseau R, Egghe L (2007) The R- and AR-indices: Complementing the h-index. Chinese Science Bulletin 52(6):855-863, doi: 10.1007/s11434-007-0145-9 . ![]() ) According to Burrell (Burrell QL (2007) On the h-index, the size of the Hirsch core and Jin's A-index. Journal of Informetrics 1(2):170-177, doi: 10.1016/j.joi.2007.01.003 .
) According to Burrell (Burrell QL (2007) On the h-index, the size of the Hirsch core and Jin's A-index. Journal of Informetrics 1(2):170-177, doi: 10.1016/j.joi.2007.01.003 . ![]() ) "the h-index seeks to identify the most productive core of an author's output in terms of most received citations". For this core, consisting of the first h papers, Rousseau (Rousseau R (2006) New developments related to the Hirsch index. Industrial Sciences and Technology, Belgium,.
) "the h-index seeks to identify the most productive core of an author's output in terms of most received citations". For this core, consisting of the first h papers, Rousseau (Rousseau R (2006) New developments related to the Hirsch index. Industrial Sciences and Technology, Belgium,. ![]() ) introduced the term Hirsch core. "The Hirsch core can be considered as a group of high-performance publications, with respect to the scientist's career". The a-index (as well as the m-index, r-index, and ar-index) includes in the calculation only papers that are in the Hirsch core. It is defined as the average number of citations of papers in the Hirsch core. The proposal to use this average number of citations as a variant of the h-index was made by Jin, the main editor of Science Focus (Jin B (2006) h-index: an evaluation indicator proposed by scientist. Science Focus 1(1):8-9). Rousseau referred to this index later as the a-index. The a-index is defined as:
) introduced the term Hirsch core. "The Hirsch core can be considered as a group of high-performance publications, with respect to the scientist's career". The a-index (as well as the m-index, r-index, and ar-index) includes in the calculation only papers that are in the Hirsch core. It is defined as the average number of citations of papers in the Hirsch core. The proposal to use this average number of citations as a variant of the h-index was made by Jin, the main editor of Science Focus (Jin B (2006) h-index: an evaluation indicator proposed by scientist. Science Focus 1(1):8-9). Rousseau referred to this index later as the a-index. The a-index is defined as:
$$A=\frac{1}{h}\displaystyle\sum_{j=1}^{h}cit_j$$
where h = h-index, and cit = citations counts.
h(2)-index: (Kosmulski M (2006) A new Hirsch-type index saves time and works equally well as the original h-index. ISSI Newsletter 2(3):4-6, . ![]() ) Like the g-index, calculation of the h(2)-index also gives more weight to highly cited articles: "A scientist's h(2)-index is defined as the highest natural number such that his h(2) most cited papers received each at least [h(2)]2 citations". An h(2)-index of 20, for example, means that a scientist has published at least 20 papers, of which each has been cited at least 400 times. Obviously, for any scientist, the h(2)-index is always lower than the h-index. According to Jin et al. (Jin BH, Liang LM, Rousseau R, Egghe L (2007) The R- and AR-indices: Complementing the h-index. Chinese Science Bulletin 52(6):855-863, doi: 10.1007/s11434-007-0145-9 .
) Like the g-index, calculation of the h(2)-index also gives more weight to highly cited articles: "A scientist's h(2)-index is defined as the highest natural number such that his h(2) most cited papers received each at least [h(2)]2 citations". An h(2)-index of 20, for example, means that a scientist has published at least 20 papers, of which each has been cited at least 400 times. Obviously, for any scientist, the h(2)-index is always lower than the h-index. According to Jin et al. (Jin BH, Liang LM, Rousseau R, Egghe L (2007) The R- and AR-indices: Complementing the h-index. Chinese Science Bulletin 52(6):855-863, doi: 10.1007/s11434-007-0145-9 . ![]() ), the main advantage of the h(2)-index is that it reduces the precision problem. That means that when computing the h(2)-index using a publication set put together for a scientist using Web of Science data (Thomson Scientific), less work is needed to check the accuracy of the publications data, especially with regard to homographs -that is, to distinguish between scientists that have the same last name and first initial- than is needed when calculating the h-index. As only few papers in the set are sufficiently highly cited in order to fulfill the criterion of [h(2)]2 citations, there are also fewer papers to check (Bornmann L, Mutz R, Daniel HD (2008) Are there better indices for evaluation purposes than the h index? A comparison of nine different variants of the h index using data from biomedicine. Journal of the American Society for Information Science and Technology 59(5):830-837, doi: 10.1002/asi.20806 .
), the main advantage of the h(2)-index is that it reduces the precision problem. That means that when computing the h(2)-index using a publication set put together for a scientist using Web of Science data (Thomson Scientific), less work is needed to check the accuracy of the publications data, especially with regard to homographs -that is, to distinguish between scientists that have the same last name and first initial- than is needed when calculating the h-index. As only few papers in the set are sufficiently highly cited in order to fulfill the criterion of [h(2)]2 citations, there are also fewer papers to check (Bornmann L, Mutz R, Daniel HD (2008) Are there better indices for evaluation purposes than the h index? A comparison of nine different variants of the h index using data from biomedicine. Journal of the American Society for Information Science and Technology 59(5):830-837, doi: 10.1002/asi.20806 . ![]() ).
).
Aggregation based indices
hg-index: (Alonso S, Cabrerizo FJ, Herrera-Viedma E, Herrera F (2010) hg-index: A new index to characterize the scientific output of researchers based on the h- and g- indices. Scientometrics 82(2):391-400 doi:10.1007/s11192-009-0047-5 . ![]() ) Alonso et al. present a new index, called hg-index, to characterize the scientific output of researchers which is based on both h-index and g-index to try to keep the advantages of both measures as well as to minimize their disadvantages. They do agree that both measures incorporate several interesting properties about the publications of a researcher and that both should be taken into account to measure the scientific output of scientists. Therefore, they present a combined index, that they call the hg-index that tries to fuse all the benefits of both previous measures and that tries to minimize the drawbacks that each one of them presented. The hg-index of a researcher is computed as the geometric mean of his h- and g- indices, that is:
) Alonso et al. present a new index, called hg-index, to characterize the scientific output of researchers which is based on both h-index and g-index to try to keep the advantages of both measures as well as to minimize their disadvantages. They do agree that both measures incorporate several interesting properties about the publications of a researcher and that both should be taken into account to measure the scientific output of scientists. Therefore, they present a combined index, that they call the hg-index that tries to fuse all the benefits of both previous measures and that tries to minimize the drawbacks that each one of them presented. The hg-index of a researcher is computed as the geometric mean of his h- and g- indices, that is:
$$hg=\sqrt{h·g}$$
It is trivial to demonstrate that h = hg = g and that hg - h = g - hg, that is, the hg-index corresponds to a value nearer to h than to g. This property can be seen as a penalization of the g-index in the cases of a very low h-index, thus avoiding the problem of the big influence that a very successful paper can introduce in the g-index.
$q^2$-index: (Cabrerizo FJ, Alonso S, Herrera-Viedma E, Herrera F (2009) q2-Index: Quantitative and Qualitative Evaluation Based on the Number and Impact of Papers in the Hirsch Core. Journal of Informetrics 4(1):23-28, doi:10.1016/j.joi.2009.06.005 . ![]() ) Cabrerizo et al. considered that as different indices measure different aspects in the scientific production of the researchers it is an interesting idea to merge some of those indices in order to obtain a simple but more complete measurement. They developed the q2-index, which is based on the geometric mean of both a quantitative measure (the h-index) and a qualitative measure (the m-index) of the h-core.
) Cabrerizo et al. considered that as different indices measure different aspects in the scientific production of the researchers it is an interesting idea to merge some of those indices in order to obtain a simple but more complete measurement. They developed the q2-index, which is based on the geometric mean of both a quantitative measure (the h-index) and a qualitative measure (the m-index) of the h-core.
$$q^2=\sqrt{h·m}$$
The h-index is used because it is robust and describes the number of the papers (quantitative dimension) in a researcher's productive core, while the m-index is used because it depicts the impact of the papers (qualitative dimension) in a researcher's productive core and because it correctly deals with citation distributions which are usually skewed. It can be noticed that the q2-index is based on two indices which stand for different dimensions of the scientist's research output. Therefore, it obtains a more global view of the scientific production of researchers.
Complementary material: Excel file with the articles/number of citations per paper for a case of study, h-index and q2-index ![]() .
.
r-index: (Jin BH, Liang LM, Rousseau R, Egghe L (2007) The R- and AR-indices: Complementing the h-index. Chinese Science Bulletin 52(6):855-863, doi: 10.1007/s11434-007-0145-9 ![]() ) Jin et al. observed criticaly that with the a-index, "the better scientist is 'punished' for having a higher h-index, as the a-index involves a division by h". Therefore, instead of dividing by h, the authors suggest taking the square root of the sum of citations in the Hirsch core to calculate the index. Jin et al. refer to this new index as the r-index, as it is calculated using a square root. As the r-index -similar to the a-index- measures the citation intensity in the Hirsch core, the index can be very sensitive to just a very few papers receiving extremely high citation counts (Bornmann L, Mutz R, Daniel HD (2008) Are there better indices for evaluation purposes than the h index? A comparison of nine different variants of the h index using data from biomedicine. Journal of the American Society for Information Science and Technology 59(5):830-837, doi: 10.1002/asi.20806
) Jin et al. observed criticaly that with the a-index, "the better scientist is 'punished' for having a higher h-index, as the a-index involves a division by h". Therefore, instead of dividing by h, the authors suggest taking the square root of the sum of citations in the Hirsch core to calculate the index. Jin et al. refer to this new index as the r-index, as it is calculated using a square root. As the r-index -similar to the a-index- measures the citation intensity in the Hirsch core, the index can be very sensitive to just a very few papers receiving extremely high citation counts (Bornmann L, Mutz R, Daniel HD (2008) Are there better indices for evaluation purposes than the h index? A comparison of nine different variants of the h index using data from biomedicine. Journal of the American Society for Information Science and Technology 59(5):830-837, doi: 10.1002/asi.20806 ![]() ). The r-index is defined as:
). The r-index is defined as:
$$R=\sqrt{\displaystyle\sum_{j=1}^{h}cit_j}$$
where h = h-index, and cit = citations counts.
ar-index: (Jin B (2007) The AR-index: complementing the h-index. ISSI Newsletter 3(1):6,. ![]() ) The ar-index is an adaptation of the r-index. It takes into account not only the citation intensity in the Hirsch core but also makes use of the age of the publications in the core. This is an index that not only can increase but also decrease over time. For a good research evaluation indicator, Jin et al. (Jin BH, Liang LM, Rousseau R, Egghe L (2007) The R- and AR-indices: Complementing the h-index. Chinese Science Bulletin 52(6):855-863, doi: 10.1007/s11434-007-0145-9 .
) The ar-index is an adaptation of the r-index. It takes into account not only the citation intensity in the Hirsch core but also makes use of the age of the publications in the core. This is an index that not only can increase but also decrease over time. For a good research evaluation indicator, Jin et al. (Jin BH, Liang LM, Rousseau R, Egghe L (2007) The R- and AR-indices: Complementing the h-index. Chinese Science Bulletin 52(6):855-863, doi: 10.1007/s11434-007-0145-9 . ![]() ) see it as a necessary condition that the index has sensitivity to performance changes. For this reason, Jin proposes the ar-index, "defined as the square root of the sum of the average number of citations per year of articles included in the h-core". To illustrate the necessity of a decreasing index in concrete application, Jin et al. calculated the h-index, r-index, and the ar-index for the articles written by BC Brookes (Brookes, who was the Derek de Solla Price Medallist in 1989, died in 1991): "Brookes' h-index over the whole period (2002-2007) stays fixed at h = 12 (hence here h > ar). Between 2002 and 2007 his r-index increased by 5% while the ar-index decreased by about 5% (Bornmann L, Mutz R, Daniel HD (2008) Are there better indices for evaluation purposes than the h index? A comparison of nine different variants of the h index using data from biomedicine. Journal of the American Society for Information Science and Technology 59(5):830-837, doi: 10.1002/asi.20806 .
) see it as a necessary condition that the index has sensitivity to performance changes. For this reason, Jin proposes the ar-index, "defined as the square root of the sum of the average number of citations per year of articles included in the h-core". To illustrate the necessity of a decreasing index in concrete application, Jin et al. calculated the h-index, r-index, and the ar-index for the articles written by BC Brookes (Brookes, who was the Derek de Solla Price Medallist in 1989, died in 1991): "Brookes' h-index over the whole period (2002-2007) stays fixed at h = 12 (hence here h > ar). Between 2002 and 2007 his r-index increased by 5% while the ar-index decreased by about 5% (Bornmann L, Mutz R, Daniel HD (2008) Are there better indices for evaluation purposes than the h index? A comparison of nine different variants of the h index using data from biomedicine. Journal of the American Society for Information Science and Technology 59(5):830-837, doi: 10.1002/asi.20806 . ![]() ). The ar-index is defined as:
). The ar-index is defined as:
$$R=\sqrt{\displaystyle\sum_{j=1}^{h}\frac{cit_j}{a_j}}$$
where h = h-index, cit = citations counts, and a = number of years since publishing.
Indices that take into account time
m quotient: (Hirsch JE (2005) An index to quantify an individual's scientific research output. Proceedings of the National Academy of Sciences 102:16569-16572, doi: 10.1073/pnas.0507655102 . ![]() ) According to a stochastic model for an author's production/citation process, Burrell (Burrell QL (2007) Hirsch's h-index: a stochastic model. Journal of Informetrics 1(1):16-25, doi: 10.1016/j.joi.2006.07.001 .
) According to a stochastic model for an author's production/citation process, Burrell (Burrell QL (2007) Hirsch's h-index: a stochastic model. Journal of Informetrics 1(1):16-25, doi: 10.1016/j.joi.2006.07.001 . ![]() ) conjectures that the h-index is approximately proportional to career length. One way to compare scientists with different lengths of scientific careers is to divide the h-index by number of years of research activity. For this reason, Hirsch already proposed dividing the h-index by number of years since a scientist's first publication and called this quotient m.
) conjectures that the h-index is approximately proportional to career length. One way to compare scientists with different lengths of scientific careers is to divide the h-index by number of years of research activity. For this reason, Hirsch already proposed dividing the h-index by number of years since a scientist's first publication and called this quotient m.
$$m quotient = \frac{h}{y}$$
where h = h-index, and y = number of years since publishing the first paper.
Contemporary h-index: (Sidiropoulos A, Katsaros D, Manolopoulos Y (2007) Generalized Hirsch h-index for disclosing latent facts in citation networks. Scientometrics 72(2):253-280, doi: 10.1007/s11192-007-1722-z ![]() ) The original h-index does not take into account the "age" of an article. It may be the case that some scientist contributed a number of significant articles that produced a large h-index, but now s/he is rather inactive or retired. Therefore, senior scientists, who keep contributing nowadays, or brilliant young scientists, who are expected to contribute a large number of significant works in the near future but now they have only a small number of important articles due to the time constraint, are not distinguished by the original h-index. Thus, it arises the need of defining a generalization of the h-index, in order to account for these facts. Therefore, a novel score $S^c(i)$ for an article i based on citation counting was defined as follows:
) The original h-index does not take into account the "age" of an article. It may be the case that some scientist contributed a number of significant articles that produced a large h-index, but now s/he is rather inactive or retired. Therefore, senior scientists, who keep contributing nowadays, or brilliant young scientists, who are expected to contribute a large number of significant works in the near future but now they have only a small number of important articles due to the time constraint, are not distinguished by the original h-index. Thus, it arises the need of defining a generalization of the h-index, in order to account for these facts. Therefore, a novel score $S^c(i)$ for an article i based on citation counting was defined as follows:
$$S^c(i)=\gamma * (Y(now)-Y(i)+1)^{-\delta}*|C(i)|$$
where Y(i) is the publication year of an article i and C(i) are the articles citing the article i. If we set d = 1, then Sc(i) is the number of citations that the article i has received, divided by the "age" of the article. Since the number of citations is divided with the time interval, the quantities Sc(i) will be too small to create a meaningful h-index; thus, the coefficient γ is used. This way, an old article gradually loses its "value", even if it still gets citations. In other words, in the calculations, we mainly take into account the newer articles. Therefore, the contemporary h-index is expressed as follows: A researcher has contemporary h-index hc if hc of its Np articles get a score of Sc(i) = hc each, and the rest (Np - hc) articles get a score of Sc(i) = hc.
Trend h-index: (Sidiropoulos A, Katsaros D, Manolopoulos Y (2007) Generalized Hirsch h-index for disclosing latent facts in citation networks. Scientometrics 72(2):253-280, doi: 10.1007/s11192-007-1722-z ![]() ) The original h-index does not take into account the year when an article acquired a particular citation, i.e., the "age" of each citation. For instance, consider a researcher who contributed to the research community a number of really brilliant articles during the decade of 1960, which, say, got a lot of citations. This researcher will have a large h-index due to the works done in the past. If these articles are not cited anymore, it is an indication of an outdated topic or an outdated solution. On the other hand, if these articles continue to be cited, then we have the case of an influential mind, whose contributions continue to shape newer scientists' minds. There is also a second very important aspect in aging the citations. There is the potential of disclosing trendsetters, i.e., scientists whose work is considered pioneering and sets out a new line of research that currently is hot ("trendy"), thus this scientist's works are cited very frequently. To handle this case, the opposite approach than the contemporary h-index's is taken. Instead of assigning to each scientist's article a decaying weight depending on its age, to each citation of an article is assigned an exponentially decaying weight, which is expressed as a function of the "age" of the citation. This way, we aim at estimating the impact of a researcher's work in a particular time instance. We are not interested in how old the articles of a researcher are, but whether they still get citations. The following equation is defined as follows:
) The original h-index does not take into account the year when an article acquired a particular citation, i.e., the "age" of each citation. For instance, consider a researcher who contributed to the research community a number of really brilliant articles during the decade of 1960, which, say, got a lot of citations. This researcher will have a large h-index due to the works done in the past. If these articles are not cited anymore, it is an indication of an outdated topic or an outdated solution. On the other hand, if these articles continue to be cited, then we have the case of an influential mind, whose contributions continue to shape newer scientists' minds. There is also a second very important aspect in aging the citations. There is the potential of disclosing trendsetters, i.e., scientists whose work is considered pioneering and sets out a new line of research that currently is hot ("trendy"), thus this scientist's works are cited very frequently. To handle this case, the opposite approach than the contemporary h-index's is taken. Instead of assigning to each scientist's article a decaying weight depending on its age, to each citation of an article is assigned an exponentially decaying weight, which is expressed as a function of the "age" of the citation. This way, we aim at estimating the impact of a researcher's work in a particular time instance. We are not interested in how old the articles of a researcher are, but whether they still get citations. The following equation is defined as follows:
$$S^t(i)=\gamma * \displaystyle\sum_{∀x\in C(i)} (Y(now)-Y(x)+1)^{-\delta}$$
where γ, d, Y(i) and S(i) for an article i are as defined as in the contemporary h-index. Therefore, the trend h-index is defined as follows: A researcher has trend h-index ht if ht of its Np articles get a score of St(i) = ht each, and the rest (Np - ht) articles get a score of St(i) = ht. Apparently, for γ = 1, d = 0, the trend h-index coincides with the original h-index.
Dynamic h-Type index: (Rousseau R, Ye FY (2008) A proposal for a dynamic h-type index. Journal of the American Society for Information Science and Technology 59(11):1853-1855, doi: 10.1002/asi.20890 ![]() ) This index depends on the h-core, the actual number of citations received by articles belonging to the h-core, and the recent increase in h. The definition contains three time-dependent elements: the size and contents of the h-core, the number of citations received, and the h-velocity. It is indeed possible that two scientists have the same h-index and the same number of citations in the h-core, but that one has no change in his h-index for a long time while the other scientist's h-index is on the rise. For hiring purposes, the second scientist is probably the better choice. Consequently, it is proposed
) This index depends on the h-core, the actual number of citations received by articles belonging to the h-core, and the recent increase in h. The definition contains three time-dependent elements: the size and contents of the h-core, the number of citations received, and the h-velocity. It is indeed possible that two scientists have the same h-index and the same number of citations in the h-core, but that one has no change in his h-index for a long time while the other scientist's h-index is on the rise. For hiring purposes, the second scientist is probably the better choice. Consequently, it is proposed
$$R(T)·V_h(T)$$
as a dynamic h-type index. Here R(T) denotes the R-index (Jin BH, Liang LM, Rousseau R, Egghe L (2007) The R- and AR-indices: Complementing the h-index. Chinese Science Bulletin 52(6):855-863, doi: 10.1007/s11434-007-0145-9 ![]() ), equal to the square root of the sum of all citations received by articles belonging to the h-core at Time T. In practice, we have to determine a starting point, T = 0, and a way of determining vh. This starting point should not be the beginning of a scientist's career, but when T is "now", then T = 0 can be taken 10 or 5 years ago (or any other appropriate time). If one has a good-fitting continuous model for h(t) over this period, then this function should be used to determine $v_h(T)$. In practice, it is probably better to find a fitting for $h_{rat}(t)$ -and not for h(t)- as this function is more similar to a continuous function than the standard h-index. Otherwise, the increment $Δh_{rat}(T)=h_{rat}(T)-h_{rat}(T-1)$ can be used (if it is not an obvious outlier). Note that when $h_{rat}(t)$ is concave, this approximation will be larger than the real derivative; when $h_{rat}(t)$ is convex, it will be smaller. When using this approximation, it is certainly appropriate to use the rational h-index as otherwise Δ(h) will often be 0 or 1, and no meaning can be attached to these values. Note that Burrell's rawh-rate h(T)/T should not be used as it is equal for all scientists with the same h(T), and hence, one loses the dynamic aspect. If equation above is actually used for evaluating purposes, self-citations should be removed.
), equal to the square root of the sum of all citations received by articles belonging to the h-core at Time T. In practice, we have to determine a starting point, T = 0, and a way of determining vh. This starting point should not be the beginning of a scientist's career, but when T is "now", then T = 0 can be taken 10 or 5 years ago (or any other appropriate time). If one has a good-fitting continuous model for h(t) over this period, then this function should be used to determine $v_h(T)$. In practice, it is probably better to find a fitting for $h_{rat}(t)$ -and not for h(t)- as this function is more similar to a continuous function than the standard h-index. Otherwise, the increment $Δh_{rat}(T)=h_{rat}(T)-h_{rat}(T-1)$ can be used (if it is not an obvious outlier). Note that when $h_{rat}(t)$ is concave, this approximation will be larger than the real derivative; when $h_{rat}(t)$ is convex, it will be smaller. When using this approximation, it is certainly appropriate to use the rational h-index as otherwise Δ(h) will often be 0 or 1, and no meaning can be attached to these values. Note that Burrell's rawh-rate h(T)/T should not be used as it is equal for all scientists with the same h(T), and hence, one loses the dynamic aspect. If equation above is actually used for evaluating purposes, self-citations should be removed.
k-index: (Ye FY, Rousseau R (2010) Probing the h-core: an investigation of the tail-core ratio for rank distributions. Scientometrics. In press, doi:10.1007/s11192-009-0099-6 ![]() ) In this recent contribution the authors worry not only about the citations in the h-core, but also in the h-tail. Thus, they defined the k-index as the ratio of impact over tail-core ratio. Moreover, the k-index was studied as a time dependant function. Concretely, being C, T, CH and CT the sets of citations, the set of publications, the set of citations receivedby the h-core and the set of citations received by the h-tail respectively, the k-index is defined as:
) In this recent contribution the authors worry not only about the citations in the h-core, but also in the h-tail. Thus, they defined the k-index as the ratio of impact over tail-core ratio. Moreover, the k-index was studied as a time dependant function. Concretely, being C, T, CH and CT the sets of citations, the set of publications, the set of citations receivedby the h-core and the set of citations received by the h-tail respectively, the k-index is defined as:
$$$k(t)=\frac{C(t)}{P(t)}/\frac{C_T(t)}{C_H(t)=\frac{C(t)C_H(t)}{P(t)(C(t)-C_H(t))}}$
Using some practical observations the authors conclude that this index decreases in most practical according to a power law model.
Seniority-independent Hirsch-type index: (Kosmulski M (2009) New seniority-independent Hirsch-type index . Journal of Informetrics 3(4):341-347, doi:10.1016/j.joi.2009.05.003 ![]() ) In this contribution the author presents an index which allows to compare the scientific output of researchers in different ages. To do so, the hdp-index is defined inthe following way: "A scientist has index hpd if hpd of his/her papers have at least hpd citations per decade each, and his/her other papers have less than hpd + 1 citations per decade each."
) In this contribution the author presents an index which allows to compare the scientific output of researchers in different ages. To do so, the hdp-index is defined inthe following way: "A scientist has index hpd if hpd of his/her papers have at least hpd citations per decade each, and his/her other papers have less than hpd + 1 citations per decade each."
Specific-impact s-index: (De Visscher A. An Index to Measure a Scientist's Specific Impact. Journal of the American Society for Information Science and Technology 61 (2) (2010) 319-328. doi:10.1002/asi.21240) This index is defined as a measure of a scientist's projected impact per paper and aims to reduce the age bias from older papers (which had more time to accumulate citations than recent papers). This index correlates well with the h-index squared.
f-index: (Franceschini F., Maisano D. Analysis of the Hirsch index's operational properties. European Journal of Operational Research 203 (2) (2010) 494-504. doi:10.1016/j.ejor.2009.08.001) This index complements the h-index with the information related to the publication age. One of its main characteristics is that it does not compromise the original simplicity and immediacy of understanding of the h-index.
Impact vitality indicator: (Rons N., Amez L. Impact vitality: an indicator based on citing publications in search of excellent scientists. Research Evaluation 18 (3) (2009) 233-241. doi:10.3152/095820209X470563) This paper contributes to the quest for an operational definition of 'research excellence' and proposes a translation of the excellence concept into a bibliometric indicator. The impact vitality indicator is proposed. It reflects the vitality of the impact of a researcher's publication output, based on the change in volume over time of the citing publications.
Other h-index related indices
m-index: (Bornmann L, Mutz R, Daniel HD (2008) Are there better indices for evaluation purposes than the h index? A comparison of nine different variants of the h index using data from biomedicine. Journal of the American Society for Information Science and Technology 59(5):830-837, doi: 10.1002/asi.20806 . ![]() ) As the distribution of citation counts is usually skewed, the median and not the arithmetic average should be used as the measure of central tendency. Therefore, as a variation of the a-index, the m-index is proposed as the median number of citations received by papers in the Hirsch core.
) As the distribution of citation counts is usually skewed, the median and not the arithmetic average should be used as the measure of central tendency. Therefore, as a variation of the a-index, the m-index is proposed as the median number of citations received by papers in the Hirsch core.
$h_w$-index: (Egghe L, Rousseau R (2008) An h-index weighted by citation impact. Information Processing and Management 44(2):770-780, doi: 10.1016/j.ipm.2007.05.003 . ![]() ) Similar to the ar-index, the $h_w$-index (an h-index weighted by citation impact) developed by Egghe and Rousseau is sensitive to performance changes. The $h_w$-index is defined as: hwindex
) Similar to the ar-index, the $h_w$-index (an h-index weighted by citation impact) developed by Egghe and Rousseau is sensitive to performance changes. The $h_w$-index is defined as: hwindex
$$h_w index = \sqrt{\displaystyle\sum_{j=1}^{r_o}{cit_j}}$$
where $r_0$ is the largest row index j such that $r_w(j)$ = $cit_j$.
hm-index: (Schreiber M (2008) To share the fame in a fair way, $h_m$ for multi-authored manuscripts. New Journal of Physics 10(040201):1-9, doi: 10.1088/1367-2630/10/4/040201 . ![]() ) the $h_m$-index which is determined in analogy to the h-index, but counting the papers fractionally according to the number of authors, for example, only as one third for three authors. This yields an effective number which is utilized to define the $h_m$-index as that effective number of papers that have been cited hm or more times. Let r be the rank that is attributed to a paper when the publication list of an author is sorted by the number c(r) of citations. This arrangement is offered, e.g. in the WoS data base. Hirsch's h-index is determined from:
) the $h_m$-index which is determined in analogy to the h-index, but counting the papers fractionally according to the number of authors, for example, only as one third for three authors. This yields an effective number which is utilized to define the $h_m$-index as that effective number of papers that have been cited hm or more times. Let r be the rank that is attributed to a paper when the publication list of an author is sorted by the number c(r) of citations. This arrangement is offered, e.g. in the WoS data base. Hirsch's h-index is determined from:
$$h=max_r(r \le c(r))$$
where each paper is fully counted for the (trivial) determination of its rank
$$r=\displaystyle\sum_{r'=1}^{r}1}
Counting a paper with a(r) authors only fractionally, i.e. by 1/a(r) yields an effective rank
$$r=\displaystyle\sum_{r'=1}^{r}\frac{1}{a(r')}
which is used to define the $h_m$-index as
$$h_m=max_r(r_{eff}(r) \le c(r))
More information about this index can be found in a recent contribution: Schreiber M (2009) A Case Study of the Modified Hirsch Index h(m) Accounting for Multiple Coauthors. Journal of the American Society for Information Science and Technology 60(6):1274-1282, doi: 10.1002/asi.21057 . ![]()
Normalized h-index: (Sidiropoulos A, Katsaros D, Manolopoulos Y (2007) Generalized Hirsch h-index for disclosing latent facts in citation networks. Scientometrics 72(2):253-280, doi: 10.1007/s11192-007-1722-z . ![]() ) Since the scientists do not publish the same number of articles, the original h-index is not the fairer metric; thus, a normalized version of h-index is defined as follows: A researcher has normalized h-index $h^n = h/N_p$, if h of its $N_p$ articles have received at least h citations each, and the rest ($N_p-h$) articles received no more than h citations.
) Since the scientists do not publish the same number of articles, the original h-index is not the fairer metric; thus, a normalized version of h-index is defined as follows: A researcher has normalized h-index $h^n = h/N_p$, if h of its $N_p$ articles have received at least h citations each, and the rest ($N_p-h$) articles received no more than h citations.
Tapered h-index: (Anderson TR, Hankin KSH, Killworth PD (2008) Beyond the Durfee square: Enhancing the h-index to score total publication output. Scientometrics 76(3):577-588, doi: 10.1007/s11192-007-2071-2 . ![]() ) Consider a scientist who has 5 publications which, when ranked, have 6,4,4,2,1 citations. This publication output can be represented by a Ferrers graph, where each row represents a partition of the total 17 cites amongst papers (Fig. 2). The largest completed (filled in) square of points in the upper left hand corner of a Ferrers graph is called the Durfee square. The h-index is equal to the length of the side of the Durfee square (in the case of Fig. 2, h = 3), effectively assigning no credit (zero score) to all points that fall outside.
) Consider a scientist who has 5 publications which, when ranked, have 6,4,4,2,1 citations. This publication output can be represented by a Ferrers graph, where each row represents a partition of the total 17 cites amongst papers (Fig. 2). The largest completed (filled in) square of points in the upper left hand corner of a Ferrers graph is called the Durfee square. The h-index is equal to the length of the side of the Durfee square (in the case of Fig. 2, h = 3), effectively assigning no credit (zero score) to all points that fall outside.
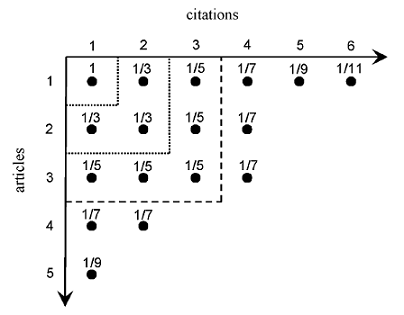
Let us start by considering h-index scores for sets of citation records that exactly match Durfee squares. If an author has a single paper that has one citation, this scores h = 1. Subsequently, h = 2 is achieved with two papers each with two citations. To move from h = 1 to h = 2, an additional 3 citations are required, one for the first paper and two for the second paper. In turn, moving from h = 2 to h = 3 requires a further 5 citations, reaching a 3, 3, 3 partitioning of the nine citations in the Ferrers graph (and so a Durfee square of side 3). Following this scheme, it is possible to score each citation individually, and in a manner that generates identical h-index scores when the relevant Durfee squares are complete (Fig. 2). Thus, the single citation in the Durfee square of side one has a score of 1, the three additional citations in the Durfee square of side 2 each score 1/3, and the five additional citations in the Durfee square of side 3 each score 1/5. Summing the relevant citations, scores of 1, 2, 3 are achieved for Durfee squares whose width is 1, 2, 3, matching the h-index. This notation immediately suggests a new index, $h_T$, which has the property that each additional citation increases the total score (the index has the property of being "marginally increasing"), whether or not it lies within the h-index Durfee square. The score of any citation on a Ferrers graph is now given by 1/(2L 1), where L is the length of side of a Durfee square whose boundary includes the citation in question. The additional citations that fall outside the Durfee square (of side 3) in Fig. 2 can now be scored, the five papers achieving scores of 1.88, 1.01, 0.74, 0.29 and 0.11, leading to a total score for $h_T$ of 4.03. In mathematical terms, the most cited paper in a given list, with $n_1$ citations, generates a score, $h_{T(1)}$, of:
$$H_{t(1)}=\displaystyle\sum_{i=1}^{n_1}\frac{1}{2i-1}=ln(n_1)/2+o(1)$$
where $ln(n_1)$ is the (natural) log of $n_1$, and o(1) is mathematical shorthand for a term that approaches zero as n1 approaches infinity. The resulting score is 2.13 for 10 citations, 3.28 for 100 citations, 4.44 for 1000 citations and 5.59 for 10000 citations (Fig. 3).
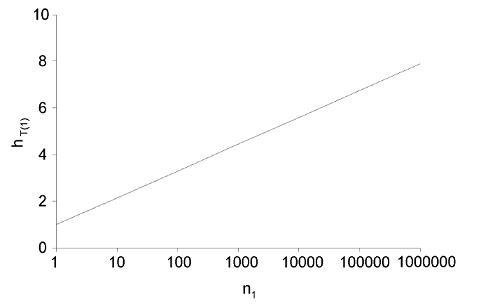
Fig. 3. Tapered h-index score for an author's top-ranked paper, $h_{T(1)}$, as a function of number of citations (n_1)
These scores are markedly higher than the score of 1 that the top-ranked paper would score for the h-index, increasing asymptotically in proportion to $log(n_1)$. The paper ranked second in the list scores 1/3 for its first citation, and then 1/3, 1/5, 1/7 etc., for further citations as for the top-ranked paper. Now, if an author has N papers with associated citations $n_1, n_2, n_3, ..., n_N$ (ranked in descending order as in a Ferrers graph), the $h_{T(1)}$ score for any single paper ranked j in the list (with $n_j$ citations), $h_{T(j)}$, is:
$$h_{T(j)}=\frac{n_j}{2j-1}, n_j \le j$$
$$h_{T(j)}=\frac{j}{2j-1}+\displaystyle\sum_{i=j+1}^{n_j}{\frac{1}{2i-1}n_j>j}$$
The total tapered h-index for a citation-ranked list of publications, $h_T$, is then calculated by summing over all the papers in the list:
$$h_T=\displaystyle\sum_{j=1}^{N}{h_T(j)}$$
$h_{rat}$-index: (Ruane F, Tol RSJ (2008) Rational (successive) h-indices: An application to economics in the Republic of Ireland. Scientometrics 75(2):395-405, doi: 10.1007/s11192-007-1869-7 . ![]() ) This index is defined as (h+1) minus the relative number of scores necessary for obtaining a value h+1. It clearly satisfies the inequality $h = h_{rat} < h+1$. More precisely, let n be the (least) number of citations necessary for obtaining an h-index 1 higher than h. This number n is divided by the highest possible n, namely, 2h+1. Indeed, the lowest possible situation leading to an h-index equal to h consists of h articles with h citations, followed by an article without any citation. To get an h-index equal to h+1, one needs one more score for each of the first h sources, h scores in total, and h+1 scores for the last one: a total of 2h+1. This h-index has the advantage of increasing in smaller steps than the standard h-index.
) This index is defined as (h+1) minus the relative number of scores necessary for obtaining a value h+1. It clearly satisfies the inequality $h = h_{rat} < h+1$. More precisely, let n be the (least) number of citations necessary for obtaining an h-index 1 higher than h. This number n is divided by the highest possible n, namely, 2h+1. Indeed, the lowest possible situation leading to an h-index equal to h consists of h articles with h citations, followed by an article without any citation. To get an h-index equal to h+1, one needs one more score for each of the first h sources, h scores in total, and h+1 scores for the last one: a total of 2h+1. This h-index has the advantage of increasing in smaller steps than the standard h-index.
v-index: (Riikonen P, Vihinen M (2008) National research contributions: A case study on Finnish biomedical research. Scientometrics. 77(2):207-222, doi:10.1007/s11192-007-1962-y . ![]() ) Riikonen and Vihinen proposed the v-index as the percentage of articles forming the h-index. They suggest that taking together the h-index and the v-index into consideration it can be better measured the recognition of scientists, and the breadth of their productivity. As the h-index grows very slowly with an increase in the number of publications, the v-index indicates great variation in the proportion of highly cited articles for PIs with similar h-index values.
) Riikonen and Vihinen proposed the v-index as the percentage of articles forming the h-index. They suggest that taking together the h-index and the v-index into consideration it can be better measured the recognition of scientists, and the breadth of their productivity. As the h-index grows very slowly with an increase in the number of publications, the v-index indicates great variation in the proportion of highly cited articles for PIs with similar h-index values.
e-index: (Zhang CT (2009) The e-Index, Complementing the h-Index for Excess Citations. PLoS ONE. 4(5):e5429, doi:10.1371/journal.pone.0005429 . ![]() ) The e-index is presented as a simple complement to the h-index. This index tries to represent the excess citations that are ignored by the h-index. One of its advantages is that it is independent of the h-index, which is not the case for almost any other related index. It's mathematical formulation is as follows:
) The e-index is presented as a simple complement to the h-index. This index tries to represent the excess citations that are ignored by the h-index. One of its advantages is that it is independent of the h-index, which is not the case for almost any other related index. It's mathematical formulation is as follows:
$$e^2=\displaystyle\sum_{j=1}^{h}{(cit_j-h)}=\displaystyle\sum_{j=1}^{h}cit_j-h^2$$
Multidimensional h-index: (Garcia-Perez MA (2009) A multidimensional extension to Hirsch's h-index. Scientometrics 81(3):779-785, doi:10.1007/s11192-009-2290-1 . ![]() ) The multidimensional h-index is defined in order to be able to discriminate among researchers with similar h-indices. To do so, the author proposes to use the papers outside the h-core to compute a succesive h-index which can help to differentiate among researchers with the same h-index. In this way, the new multidimensional h-index is able to obtain more granularity to compare scientists.
) The multidimensional h-index is defined in order to be able to discriminate among researchers with similar h-indices. To do so, the author proposes to use the papers outside the h-core to compute a succesive h-index which can help to differentiate among researchers with the same h-index. In this way, the new multidimensional h-index is able to obtain more granularity to compare scientists.
f-index: (Katsaros D, Akritidis L, Bozanis P (2009) The f Index: Quantifying the Impact of Coterminal Citations on Scientists' Ranking. Journal of the American Society for Information Science and Technology 60(5):1051-1056, doi:10.1002/asi.21040 . ![]() ) In this paper, the authors present the coterminal citations as an extension of cocitation in which some author has (co)authored multiple papers citing another paper. To avoid the impact that these coterminal citations can introduce in the h- and related indices, they propose the f-index which discriminate those individuals whose work penetrates many scienti?c communities.
) In this paper, the authors present the coterminal citations as an extension of cocitation in which some author has (co)authored multiple papers citing another paper. To avoid the impact that these coterminal citations can introduce in the h- and related indices, they propose the f-index which discriminate those individuals whose work penetrates many scienti?c communities.
π-index: (Vinkler P (2009) The π-index: a new indicator for assessing scientific impact. Journal of Information Science 35(5):602-612, doi:10.1177/0165551509103601 . ![]() ) Vinkler suggested a new index, named the π-index, for comparative assessment of scientists active in similar subject fields. The π-index is equal to one hundredth of the number of citations obtained to the top square root of the total number of journal papers ("elite set of papers") ranked by the decreasing number of citations. The author also studies the relation of the π-index to other indexes and its dependence on the field is studied, using data of journal papers of "highly cited researchers".
) Vinkler suggested a new index, named the π-index, for comparative assessment of scientists active in similar subject fields. The π-index is equal to one hundredth of the number of citations obtained to the top square root of the total number of journal papers ("elite set of papers") ranked by the decreasing number of citations. The author also studies the relation of the π-index to other indexes and its dependence on the field is studied, using data of journal papers of "highly cited researchers".
RC- and CC- indices: (Abbasi A., Altmann J., Hwang J. Evaluating scholars based on their academic collaboration activities: two indices, the RC-index and the CC-index, for quantifying collaboration activities of researchers and scientific communities. Scientometrics 83 (1) (2010) 1-13. doi:10.1007/s11192-009-0139-2) This study addresses the problem of the evaluation of the collaboration activities of researchers. Based on three measures, namely the collaboration network structure of researchers, the number of collaborations with other researchers, and the productivity index of co-authors, two new indices, the RC-Index and CC-Index, are proposed for quantifying the collaboration activities of researchers and scientific communities.
ch-index: (Ajiferuke I., Wolfram D. Citer analysis as a measure of research impact: library and information science as a case study. Scientometrics 83 (3) (2010) 623-638. doi:10.1007/s11192-009-0127-6) This paper proposes to use the number of citers instead of citations for the researcher production. Thus, it is possible to obtain a complementary measure of the author's reach of influence in a field, minimizing the effects of a limited circle of researchers citing the author's works.
Citation speed s-index: (Bornmann L., Daniel H.D. The citation speed index: A useful bibliometric indicator to add to the h index. Journal of Informetrics 4 (3) (2010) 444-446. doi:10.1016/j.joi.2010.03.007) This proposal is constructed as a meaningful complement to the h-index. It uses the number of months that have elapsed since the first citation. It tries to reflect the reception of the publications by the scientific community. Particularly, the speed index is defined as: a group of papers has the index s if for s of its $N_p$ papers the first citation was at least s months ago, and for the other ($N_p − s$) papers the first citation was ≤ s months ago.
$h^2$-lower, $h^2$-center and $h^2$-upper: (Bornmann L., Mutz R., Daniel H.D. The h index research output measurement: Two approaches to enhance its accuracy. Journal of Informetrics 4 (3) (2010) 407-414. doi:10.1016/j.joi.2010.03.005) In this work the authors address the problem that the h-index (and many of its variants) center its attention in just a portion of the scientist's citation distribution. To avoid this problem the authors define three h variants to quantify three different areas in the scientist's citation distribution: the low impact area ($h^2$-lower), the area captured by the h index ($h^2$-center), and the area of publications with the highest visibility ($h^2$-upper).
Environment $H_j$-indices (Dorta-Gonzalez P., Dorta-Gonzalez M.I. Bibliometric indicator based on the h-index. Revista Española de Documentación Científica 33 (2) (2010) 225-245. doi:10.3989/redc.2010.2.733) These indices are introduced to help to discriminate among similar index values (for example, when two citation curves intersect each other). The main idea of this index is to take into account the areas above and under the h-square in the citation curve when the h-index is increased. Thus, it is able to better discriminate among researchers with similar h-indices but different citation distributions.
h̄-index (Hirsch J.E. An index to quantify an individual's scientific research output that takes into account the effect of multiple coauthorship. Scientometrics 85 (3) (2010) 741-754. doi:10.1007/s11192-010-0193-9) In this recent proposal, Hirsch presents the h̄-index ("hbar"), defined as the number of papers of an individual that have citation count larger than or equal to the h̄ of all coauthors of each paper. This new index is useful to characterize the scientific output of a researcher that taking into account the effect of multiple authorship.
Role based h-maj-index (Hu X.J., Rousseau R., Chen J. In those fields where multiple authorship is the rule, the h-index should be supplemented by role-based h-indices. Journal of Information Science 36 (1) (2010) 73-85. doi:10.1177/0165551509348133) As with other recent proposals, the authors are dealing with the problem of multiple co-authorship. In this paper they propose a new index which is computed as the h-index but only on the papers in which the author has played a major or core role. The authors suggest that it can be used as a supplementary index in the fields where "first authors" and / or "corresponding authors" are common.
2nd generation citations h-index (Kosmulski M. Hirsch-type approach to the 2nd generation citations. Journal of Informetrics 4 (3) (2010) 257-264. doi:10.1016/j.joi.2010.01.003) An alternative h-index where the 2nd generation citations (citations to the papers that cite a paper) is presented. This approach allows to better rate the papers as not all direct citations do have the same weight.
n-index (Namazi M.R., Fallahzadeh M.K. n-index: A novel and easily-calculable parameter for comparison of researchers working in different scientific fields. Indian Journal of Dermatology Venereology & Leprology 76 (3) (2010) 229-230. doi:10.4103/0378-6323.62960) The n-index is presented as an easy solution for the comparison of researchers working on different disciplines. To do so, the n-index is computed as the researcher's h-index divided by the highest h-index of the journals of his/her major field of study.
p-index (Prathap G. The 100 most prolific economists using the p-index. Scientometrics 84 (1) (2010) 167-172. doi:10.1007/s11192-009-0068-0) The author critics the h-index as it is a poor indicator of performance. To overcome this issue a new index, the performance p-index is presented. It is defined as to provide the best balance between activity (total citations) and excellence (mean citation rate). The author uses this new indicator to rank the 100 most prolific economists.
Mock $h_m$-index (Prathap G. Is there a place for a mock h-index?. Scientometrics 84 (1) (2010) 153-165. doi:10.1007/s11192-009-0066-2) A new index is proposed in order to enhace the resolving power of the original h-index. It has been designed using ideas from mathematical modeling.
w-index (Wu Q. The w-Index: A Measure to Assess Scientific Impact by Focusing on Widely Cited Papers. Journal of the American Society for Information Science and Technology 61 (3) (2010) 609-614. doi:10.1002/asi.21276) The w-index is defined in a similar way to the h-index but focusing only in excellent papers (or highly cited papers). To do so it is defined as: If w of a researcher's papers have at least 10w citations each and the other papers have fewer than 10(w+1) citations, that researcher's w-index is w. The author shows that there are noticeable diffeerences among the h- and w- indices as the w-index plays close attention to the more widely cited papers.
b-index (Brown R.J.C. A simple method for excluding self-citation from the h-index: the b-index. Online Information Review 33 (6) (2009) 1129-1136. doi:10.1108/14684520911011043) The author addresses the problem of self-citations inflating h- related indices. To do so he assumes that relative self-citation rate is constant across an author's publications and that the citation profile of a set of papers follows a Zipfian distribution. It is shown that a value called the b-index can be computed as the integer value of the author's external citation rate (non-self-citations) to the power three quarters, multiplied by their h-index. This value, does not require an extensive analysis of the self-citation rates of individual papers to produce, and appropriately shows the biggest numerical decreases, as compared to the corresponding h-index, for very high self-citers and thus, the presented method allows the user to assess quickly and simply the effects of self-citation on an author's h-index.
Generalized h-index (Glanzel W., Schubert A. Hirsch-type characteristics of the tail of distributions. The generalised h-index. Journal of Informetrics 4 (1) (2009) 118-123. doi:10.1016/j.joi.2009.10.002) In this paper a generalisation of the h-index and g-index is given on the basis of non-negative real-valued functionals defined on subspaces of the vector space generated by the ordered samples. Several Hirsch-type measures are defined and their basic properties are analysed.
w-index (Wohlin C. A new index for the citation curve of researchers. Scientometrics 81 (2)(2009) 521-533. doi:10.1007/s11192-008-2155-z) In this paper is reflected that usual citation indexes as the h-index reduce the distribution of cites into a single point estimation, which can be seen as an over-simplification. Thus, he proposes and new index that takes into account the whole citation curve of the researcher. He conlcudes that the new index provides an added value as it balances citations and publications through the citation curve.
h-related indices to evaluate scientific production at different levels
$IF2^$-index: ( Journal Impact Factors for evaluating scientific performance: use of h-like indicators. Scientometrics 82 (3) (2010) 613-626. doi:10.1007/s11192-010-0175-y) The Impact Factor squared index is presented in order to reflect the degree in which large entities (countries or states) participate in top-level research in a particular field. It uses the Journal Impact Factor instead of the number of citations and can be extended to other h-related indices. It's main advantages are: i) it provides a stable value that does not change over time, reflecting the degree to which a research unit participated in top-level research in a given year; ii) it can be calculated closely approximating the publication date of yearly datasets; iii) it provides an additional dimension when a full article-based citation analysis is not feasible.
Single paper h-index: ( Using the h-index for assessing single publications. Scientometrics 78 (3) (2009) 559-565. doi:10.1007/s11192-008-2208-3 ) This index is a simple extension to measure the direct impact of highly cited publication as well as its indirect influence through the citing papers. It is computed as the h-index of the set of papers citing the work in question.
hint-index: ( Hirsch-type index of international recognition. Journal of Informetrics 4 (3) (2010) 351-357. doi:10.1016/j.joi.2010.02.004) This index tries to measure the broad international recognition of a scientist. To do so it uses the number of countries of the citing papers instead of the number of citations for a paper. One of its advantages is that it prevents the overrating of a citation record by self-citations or citations of a narrow circle of co-workers.
mean h-index: ( Ranking university departments using the mean h-index. Scientometrics 82 (2) (2010) 211-216. doi:10.1007/s11192-009-0048-4) In this work the autor proposed that to rank universities. To do so it computes the h-index to some related departments in each university and the mean of those evaluations is used to rank the research performance of the university in a particular field.
$^nh_3$-index: ( A research impact indicator for institutions. Journal of Informetrics 4 (4) (2010) 581-590. doi:10.1016/j.joi.2010.06.006) The authors present another index to assess the scientific production of institutions. Their main argument is that using just the h-index (based on the number of citations and documents) to measure this performance produce a very institution size biased result. Furthermore, the h-index when applied to institutions tends to retain a very small number of documents making all other research production irrelevant for this indicator. The nh3 index proposed here is designed to measure solely the impact of research in a way that is independent of the size of the institution and is made relatively stable by making a 20-year estimate of the citations of the documents produced in a single year.
πv-index: ( The pi(v)-index: a new indicator to characterize the impact of journals. Scientometrics 82 (3) (2010) 461-475. doi:10.1007/s11192-010-0182-z) Vinkler presents a new indicator stressing the importance of papers in the "elite set" (i.e., highly cited papers). The number of papers in the elite set (P πv) is calculated with the equation: (10 log P) − 10, where P is the total number of papers in the set. The one-hundredth of citations (C) obtained by P πv papers is regarded as the πv-index which is field and time dependent. The πv-index is closely correlated with the citedness (C/P) of P πv papers, and it is also correlated with the Hirsch-index.
Standarization of the h-index for comparing scientific that work in different scientific fields
(Iglesias JE, Pecharromán C (2007) Scaling the h-index for different scientific ISI fields. Scientometrics 73(3):303-320, doi: 10.1007/s11192-007-1805-x . ![]() ) That the h-index cannot be used off-hand to compare research workers of different areas has been pointed out by Hirsch himself, by noting that the most highly cited scientists for the period 1983-2002 in the life sciences had h values that were almost twice those of the most cited physicists; and from a list of the 36 inductees in the US National Academy of Sciences in the biological and biomedical sciences he extracts the same trend, although perhaps with smaller relative differences with respect to the physical sciences. It is also well known that the usual journal citation indicators lack normalisation for reference practices and traditions in the different fields of science (Pinski G, Narin F (1976) Citation influence for journal aggregates of scientific publications: theory, with application to the literature of physics. Information Processing and Management 12(5):297-312, doi: 10.1016/0306-4573(76)90048-0 .
) That the h-index cannot be used off-hand to compare research workers of different areas has been pointed out by Hirsch himself, by noting that the most highly cited scientists for the period 1983-2002 in the life sciences had h values that were almost twice those of the most cited physicists; and from a list of the 36 inductees in the US National Academy of Sciences in the biological and biomedical sciences he extracts the same trend, although perhaps with smaller relative differences with respect to the physical sciences. It is also well known that the usual journal citation indicators lack normalisation for reference practices and traditions in the different fields of science (Pinski G, Narin F (1976) Citation influence for journal aggregates of scientific publications: theory, with application to the literature of physics. Information Processing and Management 12(5):297-312, doi: 10.1016/0306-4573(76)90048-0 . ![]() ; Glänzel W, Moed HF (2002) Journal impact measures in bibliometric research. Scientometrics 53(2):171-193, doi: 10.1023/A:1014848323806 .
; Glänzel W, Moed HF (2002) Journal impact measures in bibliometric research. Scientometrics 53(2):171-193, doi: 10.1023/A:1014848323806 . ![]() ), among other flaws that have been pointed out in the specialised literature. Therefore, it should come as no surprise that the h-index is also flawed in similar ways. For this reason, different standardizations of the h-index for comparing scientists that work in different scientific fields have been developed.
), among other flaws that have been pointed out in the specialised literature. Therefore, it should come as no surprise that the h-index is also flawed in similar ways. For this reason, different standardizations of the h-index for comparing scientists that work in different scientific fields have been developed.
Iglesias JE, Pecharromán C (2007) Scaling the h-index for different scientific ISI fields. Scientometrics 73:(3):303-320, doi: 10.1007/s11192-007-1805-x . ![]()
In this paper, the authors suggest a rational method to account for different citation practices, introducing a simple multiplicative correction to the h-index which depends basically on the ISI field the worker is in, and to some extent, on the number of papers the researcher has published. They also propose a list of these normalizing factors, so the corrected h remains relatively simple to obtain.
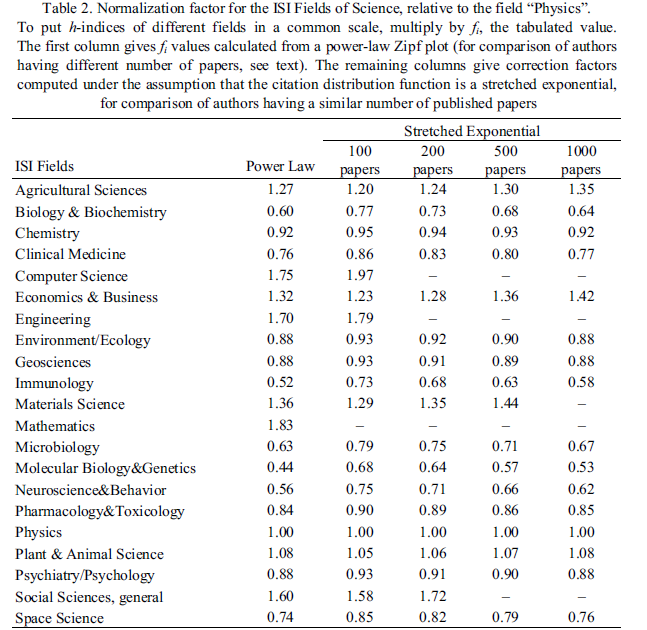
Imperial J, Rodríguez-Navarro A (2007) Usefulness of Hirsch's h-index to evaluate scientific research in Spain. Scientometrics 71(2):271-282, doi: 10.1007/s11192-007-1665-4 . ![]()
In this paper, the authors suggest that, in general, publications in applied areas are less cited that publications in dynamic, basic areas, and therefore, scientists in the former areas show lower values of h. These differences are mainly caused by: (i) the different sizes of the populations that can potentially cite the publication, and (ii) the lower emphasis placed on research by scientists in applied areas. Although the complex dependence of h on the citing population size precludes an overall h normalization across scientific areas, they empirically observed that the highest h values attained for a given area correlate well with the impact factor of journals in that area. They calculated h-indexes for the most highly cited scientists in different areas and subareas (reference h-index or hR) and observed that hR indexes are more dependent on journal impact factors than on specific publication patterns. In general, and for most areas, they observe
$$h_R \sim 16+11f$$
where f is the impact factor of the top journals that characterize that specific scientific area or subarea. Since hR exhibits a linear dependence on f, it is possible to compute it as an average for scientists who publish in more than one area.
Namazi M.R., Fallahzadeh M.K. n-index: A novel and easily-calculable parameter for comparison of researchers working in different scientific fields. Indian Journal of Dermatology Venereology & Leprology 76 (3) (2010) 229-230. doi: 10.4103/0378-6323.62960
The n-index is presented as an easy solution for the comparison of researchers working on different disciplines. To do so, the n-index is computed as the researcher's h-index divided by the highest h-index of the journals of his/her major field of study.
Some studies analyzing the indices
Studies comparing h-index and other bibliometric indicators
Bornmann L, Wallon G, Ledin A (2008) Is the h index related to (standard) bibliometric measures and to the assessments by peers? An investigation of the h index by using molecular life sciences data. Research Evaluation 17(2):149-156, doi: 10.3152/095820208X319166
In this paper, the authors used some comprehensive data sets of applicants to the long-term fellowship and young investigator programmes of the European Molecular Biology Organization. They determined the relationship between the h-index and three standard bibliometric indicators (total number of publications, total citation counts, and average journal impact factor) as well as peer assessments to test the convergent validity of the h-index. Their results suggest that the h-index is a promising rough measurement of the quality of a young scientist's work as it is judged by internationally renowned scientists.
Costas R, Bordons M (2008) Is g-index better than h-index? An exploratory study at the individual level. Scientometrics 77(2):267-288, doi: 10.1007/s11192-007-1997-0 ![]()
In this paper, the authors analyse the ability of g-index and h-index to discriminate between different types of scientists (low producers, big producers, selective scientists and top scientists) in the area of Natural Resources at the Spanish CSIC (WoS, 1994-2004). Their results show that these indicators clearly differentiate low producers and top scientists, but do not discriminate between selective scientists and big producers. However, they show that g-index is more sensitive than h-index in the assessment of selective scientists, since this type of scientist shows in average a higher g-index/h-index ratio and a better position in g-index rankings than in the h-index ones. Therefore, current research suggests that these indexes do not substitute each other but that they are complementary.
Lehmann S, Jackson AD, Lautrup BE (2008) A quantitative analysis of indicators of scientific performance. Scientometrics 76(2):369-390, doi: 10.1007/s11192-007-1868-8 ![]()
In this work, some Bayesian statistics are used in order to analyze the h-index and several other different indicators of scientific performance to try determine each indicator's ability to discriminate between scientific authors. They demonstrate that the best of the indicators that they studied requires approximately 50 papers to draw conclusions regarding long term scientific performance. In addition, they stated how their approach allows a statistical comparison among scientists from different fields.
Van Leeuwen T (2008) Testing the validity of the Hirsch-index for research assessment purposes. Research Evaluation 17(2):157-160, doi: 10.3152/095820208X319175
A bibliometric study in the Netherlands has been conducted focusing on the level of the individual researcher in relation to an academic reward system. He compared the h-index with various bibliometric indicators and other characteristics of researchers and tested its usefulness in research assessment procedures. He found that there is a strong bias towards the research field(s) in which the researcher is active, and thus, he concludes that this limits the validity of the h-index for the specific interest of evaluation practices.
Zhang CT (2009) The e-Index, Complementing the h-Index for Excess Citations. PLoS ONE. 4(5):e5429, doi:10.1371/journal.pone.0005429 ![]()
In the article where Zhang defined the e-index he also introduces some comparisons between the new index and some classical ones (the r-index, a-index and g-index). In this comparison the author is particulary concerned about the possible loss of citation information of the g-index.
Burrell QL (2009) On Hirsch's h, Egghe's g and Kosmulski's h(2). Scientometrics 79(1):79-91, doi:10.1007/s11192-009-0405-3 ![]()
The paper investigates the inter-relationships between the h-index, the g-index and the h(2)-index and also their time dependence using the stochastic publication/citation model previously proposed by the author. Some tentative suggestions regarding the relative merits of these three proposed measures are also presented.
Guns R, Rousseau R (2009) Real and rational variants of the h-index and the g-index. Journal of Informetrics 3(1):64-71, doi:10.1016/j.joi.2008.11.004 ![]()
In this contribution the authors review the definitions of the rational and real-valued variants of the h-index and g-index. They showed how they can be obtained both graphically and by calculation. In addition they show that the relation between the real and the rational g-index depends on the number of citations of the article ranked g + 1.
Bador P., Lafouge T. Comparative Analysis of Impact Factor and h-index for Pharmacology Journals. Therapie 65 (2) (2010) 129-137, doi:10.2515/therapie/2009061
The authors compare the Impact Factor (IF) 2006 and the h-index 2006 for one sample of "Pharmacology and Pharmacy" journals computed from the ISI Web of Science using the same parameters (identical two publication years (2004-2005) and identical one-year citation window (2006)). They concluded that the IF and the h-index rankings of the journals are very different (the correlation coefficient between the IF and the h-index is low for this area journals). The IF and h-index can be completely complementary when evaluating journals of the same scientific discipline. This study has been leater complemented in Bador P., Lafouge T. Comparative analysis between impact factor and h-index for pharmacology and psychiatry journals. Scientometrics 84 (1) (2010) 65-79, doi:10.1007/s11192-009-0058-2
Abramo G., D'Angelo C.A., Viel F. A Robust Benchmark for the h- and g-Indexes. Journal of the American Society for Information Science and Technology 61 (6) (2010) 1275-1280, doi:10.1002/asi.21330
This paper aims to provide some light on the problem of comparison of h- related indices among different scientists. To do so the authors have measured the h- and Egghe's g-indexes of all Italian university researchers in the hard sciences over a 5-year window. Descriptive statistics are provided concerning all of the 165 subject fields examined, offering robust benchmarks for those who wish to compare their individual performance to those of their colleagues in the same subject field.
Studies that analyze h- based indices and their correlations
Schreiber M (2008) An empirical investigation of the g-index for 26 physicists in comparison with the h-index, the a-index, and the r-index. Journal of the American Society for Information Science and Technology, 59(9):1513-1522, doi: 10.1002/asi.20856 ![]()
In this study, Schreiber works out 26 practical cases of physicists from the Institute of Physics at Chemnitz University of Technology, and compare the h and g values. It is demonstrated that the g-index discriminates better between different citation patterns. As expected, the g-index allows for a better discrimination between the datasets and yields some rearrangement of the order. The rearrangements can be traced to different individual citation patterns, in particular distinguishing between one-hit wonders and enduring performers: The one-hit wonders advance in the g-sorted list. In his opinion, this makes the g-index more suitable than the h-index to characterize the overall impact of the publications of a scientist. Especially for not-so-prominent scientists, the small values of h do not allow for a reasonable distinction between the datasets. This also can be achieved by evaluating the a-index, which reflects the average number of citations in the h-core, and interpreting it in conjunction with the h-index. h and a can be combined into the r-index to measure the hcore's citation intensity. He also determines the a and r values for the 26 datasets. For a better comparison, he utilizes interpolated indices. The correlations between the various indices as well as with the total number of papers and the highest citation counts are discussed. The largest Pearson correlation coefficient is found between g and r. Although the correlation between g and h is relatively strong, the arrangement of the datasets is significantly different depending on whether they are put into order according to the values of either h or g.
Bornmann L, Mutz R, Daniel HD (2008) Are there better indices for evaluation purposes than the h index? A comparison of nine different variants of the h index using data from biomedicine. Journal of the American Society for Information Science and Technology 59(5):830-837, doi: 10.1002/asi.20806 ![]()
In this study, the authors examined empirical results on the h-index and its most important variants in order to determine whether the variants developed are associated with an incremental contribution for evaluation purposes. They examined the h-index and the most important h-index variants, that have been proposed and discussed in the literature: the m quotient, g-index, h(2)-index, a-index, r-index, ar-index and hw-index. They also included in their analysis the m-index, a variant that we propose of the a-index. The aim of the analysis is to determine empirically the extent to which the development of the variants of the h-index does in fact result in an incremental contribution. The results of the analysis indicate that with the h-index and its variants, we can assume that there are two types of indices: (i) The one type of indices (h-index, m quotient, g-index and h(2)-index) describe the most productive core of the output of a scientist and tell us the number of papers in the core, and (ii) the other indices (a-index, m-index, r-index, ar-index and hw-index) depict the impact of the papers in the core.
Bornmann L, Marx W, Schier H (2009) Hirsch-type index values for organic chemistry journals: a comparison of new metrics with the Journal Impact Factor. European Journal of Organic Chemistry 10:1471-1476, doi: 10.1002/ejoc.200801243 ![]()
Further empirical analysis on the h-index and several of its variants (g-index, h(2)-index, a-index and r-index) to measure the performance of journals is presented in this work. Concretely, the authors compare 20 organic chemistry journals with those indices and with the Journal Impact Factor and they found very high intercorrelations among all indices. Thus, the authors conclude that all the examined measures could be called redundant for empirical applications.
Costas R, Bordons M (2008) Is g-index better than h-index? An exploratory study at the individual level. Scientometrics 77(2):267-288, doi: 10.1007/s11192-007-1997-0 ![]()
In this paper, the authors analyse the ability of g-index and h-index to discriminate between different types of scientists (low producers, big producers, selective scientists and top scientists) in the area of Natural Resources at the Spanish CSIC (WoS, 1994-2004). Their results show that these indicators clearly differentiate low producers and top scientists, but do not discriminate between selective scientists and big producers. However, they show that g-index is more sensitive than h-index in the assessment of selective scientists, since this type of scientist shows in average a higher g-index/h-index ratio and a better position in g-index rankings than in the h-index ones. Therefore, current research suggests that these indexes do not substitute each other but that they are complementary.
Costas R, Bordons M (2007) Advantages, limitations and its relation with other bibliometric indacators at the micro level. Journal of Informetrics 1(3):193-203, doi: 10.1016/j.joi.2007.02.001 ![]()
The relationship of the h-index with other bibliometric indicators at the micro level is analysed for Spanish CSIC scientists in Natural Resources, using publications downloaded from the Web of Science (1994-2004). Different activity and impact indicators are obtained to describe the research performance of scientists in different dimensions, being the h-index located through factor analysis in a quantitative dimension highly correlated with the absolute number of publications and citations. The need to include the remaining dimensions in the analysis of research performance of scientists and the risks of relying only on the h-index are stressed. The hypothesis that the achievement of some highly visible but intermediate-productive authors might be underestimated when compared with other scientists by means of the h-index is tested. The authors suggest that the h-index tends to underestimate the achievement of scientists with a "selective publication strategy", that is, those who do not publish a high number of documents but who achieve a very important international impact. In addition, a good correlation is found between the h-index and other bibliometric indicators, especially the number of documents and citations received by scientists, that is, the best correlation is found with absolute indicators of quantity. Finally, they notice that The widespread use of the h-index in the assessment of scientists' careers might influence their publication behaviour. It could foster productivity instead of promoting quality, and it may be increasing the presence of least publishable units or salami publications, since the maximum h-index an author can obtain is that of his/her total number of publications.
Schubert A, Glanzel W (2007) A systematic analysis of Hirsch-type indices for journals. Journal of Informetrics 1(3):179-256, doi: 10.1016/j.joi.2006.12.002 ![]()
In this paper, the authors presented a theoretical model of the dependence of h- related indices on the number of publications and the average citation rate. They successfully tested it against some empirical samples of journal h-indices. Their results demostrated that it is possible to stablish a kind of "similarity transformation" of h-indices between different fields of science. More information about this model compared to others can be found in:
Ye FY (2009) An investigation on mathematical models of the h-index. Scientometrics 81(2):493-498, doi: 10.1007/s11192-008-2169-6 ![]()
Bar-Ilan J. Rankings of information and library science journals by JIF and by h-type indices. Journal of Informetrics 4 (2) (2010) 141-147, doi:10.1016/j.joi.2009.11.006
In this paper we compute journal rankings in the Information and Library Science JCR category according to the JIF and according to several h-type indices. Even though the correlations between all the ranked lists are very high, there are considerable individual differences between the rankings as can be seen by visual inspection, showing that the correlation measure is not sensitive enough. Spearman's footrule and the M-measure are also computed and found to be more sensitive to the differences between the rankings in the sense that the range of values is larger than the range of correlation values when comparing the JIF ranking to the rankings induced by the h-type indices.
Leydesdorff L. How are New Citation-Based Journal Indicators Adding to the Bibliometric Toolbox?. Journal of the American of the American Society for Information Science and Technology 60 (7) (2009) 1327-1336, doi:10.1002/asi.21024
The paper studies how some of the new indicators for research assessments increments knowledge about scientific production. Particularly the author studies the h-index, the PageRank indicator and the Scimago Journal Ranking indicator.
Liu Y.X., Rousseau R. Properties of Hirsch-type indices: the case of library classification categories. Scientometrics 79 (2) (2009) 235-248, doi:10.1142/10.1007/s11192-009-0415-1
In this contribution the h-, g- and R- indices are found to be statistically equivalent for rankings of library classification categories. Moreover, the suthors found that the discrimination power of those indices are equivalent as measured by the Gini concentration index.
Schreiber M. Twenty Hirsch index variants and other indicators giving more or less preference to highly cited papers. Annalen der Physik 19 (8) (2010) 536-554, doi:10.1002/andp.201000046
This paper presents an empirical study about 26 physicists and compares different h-index variants (A, e, f, g, h(2), hw, hT, h̄, m, π, R, s, t, w, maxprod...). The author discusses the correlation among the results.
Studies about how self-citation affect the h-index
Schreiber M (2007) Self-citation corrections for the Hirsch index. Epl 78(3):30002, doi: 10.1209/0295-5075/78/30002 ![]()
In this paper, Schreiber studies several anonymous datasets concludes that self-citations do have a great impact on the h-index, specially in the case of young scientists with a low h-index. Moreover, he proposes three different ways to sharpen the h-index to avoid the self-citation problem. Each proposal has an increasing level of difficulty as usual citation databases do not allow to easily differentiate among self-citations and external citation.
Schreiber M (2008) The influence of self-citation corrections on Egghe's g index. Scientometrics 76(1):187-200, doi: 10.1007/s11192-007-1886-6 ![]()
In a later work, Schreiber again studies how both the h- and g- indices are affected by self citations by means of an analysis of nine practical cases in the physics field. He concludes that the g-index is more influenced by self-citations than the h-index and thus, he proposes to exclude those citations in the computation of the g-index.
Engqvist L, Frommen JG (2008) The h-index and self-citations. Trends in Ecology & Evolution 23(5):250-252, doi: 10.1016/j.tree.2008.01.009 ![]()
In this case, the authors argue that to increase one's own h-index would be necessary to cite many self papers and that it is difficult to predict which papers should be cited in order to improve the author's h-index. In fact, they performed a literature study, selecting 40 authors from the fields of evolutionary biology and ecology and identified the citation causing their most recent increases in h. Next, they distinguished the first citation appearing thereafter, which would have caused the same increase in the author's h. The difference between the publication dates of these two citations give the time that the h-index is dependent on one single citation. This timemeasure is an estimation of how long selective self-citation of target papers would be effective.
Gianoli E, Molina-Montenegro MA (2009) Insights Into the Relationship Between the h-Index and Self-Citations. Journal of the American Society for Information Science and Technology 60(6):1283-1285, doi: 10.1002/asi.21042 ![]()
Analyzing the publication output of 119 Chilean ecologists the authors found strong evidence that self-citations significantly affect the h-index increase, specially among the low h-index group, where self-citations cause the greater impact.
Costas R., van Leeuwen T.N., Bordons M. Self-citations at the meso and individual levels: effects of different calculation methods. Scientomtrics 82 (3) (2010) 517-537, doi: 10.1007/s11192-010-0187-7
The authors focus on the study of self-citations at the individual levels, on the basis of an analysis of the production (1994–2004) of individual researchers working at the Spanish CSIC in the areas of Biology and Biomedicine and Material Sciences. They described two different types of self-citations: author self-citations (citations received from the author him/herself) and co-author self-citations (citations received from the researchers' co-authors but without his/her participation). They conclude that self-citations do not play a decisive role in the high citation scores of documents either at the individual or at the meso level, which are mainly due to external citations.
Egghe L. Influence of Adding or Deleting Items and Sources on the H-Index. Journal of the American Society for Information Science and Technology 61 (2) (2010) 370-373, doi: 10.1002/asi.21239
Egghe discusses the mathematical influence of adding or deleting items in the computation of the h-index of an author. Thus, he proves how self-citations or minor contributions contribute to the h-index. Moreover, this influence is modelled in the paper.
Engqvist L., Frommen J.G. New Insights Into the Relationship Between the h-Index and Self-Citations?. Journal of the American Society for Information Science and Technology 61 (7) (2010) 1514-1515, doi: 10.1002/asi.21298
MacRoberts M.H., MacRoberts B.R. Problems of citation analysis: A study of uncited and seldom-cited influences. Journal of the American Society for Information Science and Technology 61 (1) (2010) 1-12, doi: 10.1002/asi.21228
The authors examined articles in biogeography and found that most of the influence is not cited, specific types of articles that are influential are cited while other types of that also are influential are not cited, and work that is "uncited" and "seldom cited" is used extensively. As a result, they propose that evaluative citation analysis should take uncited work into account.
Brown R.J.C. A simple method for excluding self-citation from the h-index: the b-index. Online Information Review 33 (6) (2009) 1129-1136, doi: 10.1108/14684520911011043
The author addresses the problem of self-citations inflating h- related indices. To do so he assumes that relative self-citation rate is constant across an author's publications and that the citation profile of a set of papers follows a Zipfian distribution. It is shown that a value called the b-index can be computed as the integer value of the author's external citation rate (non-self-citations) to the power three quarters, multiplied by their h-index. This value, does not require an extensive analysis of the self-citation rates of individual papers to produce, and appropriately shows the biggest numerical decreases, as compared to the corresponding h-index, for very high self-citers and thus, the presented method allows the user to assess quickly and simply the effects of self-citation on an author's h-index.
Studies that stablish some axioms and mathematical interpretations of h- based indices
Woeginger GJ (2008) An axiomatic characterization of the Hirsch-index. Mathematical Social Sciences 56(2):224-232, doi: 10.1016/j.mathsocsci.2008.03.001 ![]()
In this paper a new axiomatic characterization of the h-index in terms of three natural axioms (concerning the addition of single publications, the addition of new citations to old publications and the joint case of adding new publications and citations) is provided. Some extensions to this work can be found in:
Woeginger GJ (2008) A symmetry axiom for scientific impact indices. Journal of Informetrics 2(4):298-303, doi: 10.1016/j.joi.2008.09.001 ![]()
Woeginger GJ (2008) Generalizations of Egghe's g-Index. Journal of the American Society for Information Science and Technology 60(6):1267-1273, doi: 10.1002/asi.21061 ![]()
Rousseau R (2008) Woeginger's axiomatisation of the h-index and its relation to the g-index, the h(2)-index and the R2-index. Journal of Informetrics 2(4):263-372, doi: 10.1016/j.joi.2008.07.001 ![]()
Torra V, Narukawa Y (2008) The h-index and the number of citations: Two fuzzy integrals. IEEE Transactions on Fuzzy Systems 16(3):795-797, doi: 10.1109/TFUZZ.2007.896327 ![]()
In this work, the authors have stablished the connection of the h-index (and the number of citations) with the Choquet and Sugeno integrals. In particular they showthat the h-index is a particular case of the Sugeno integral and that the number of citations corresponds to the Choquet integral (in both cases using the same fuzzy measure). This conclusion allows the authors to envision new indexes defined in terms of fuzzy integrals using different types of fuzzy measures. This work is extended in:
Narukawa Y, Torra V (2009) Multidimensional generalized fuzzy integral. Fuzzy Sets and Systems 160(6):802-815, doi: 10.1016/j.fss.2008.10.006 ![]()
Liang LM (2006) h-index sequence and h-index matrix: Constructions and applications. Scientometrics 69(1):153-159, doi: 10.1007/s11192-006-0145-6 ![]()
In this early paper, Liang studied how the h-index changes over time using time series. After his initial work there have been several studies about time series, the h-index and its mathematical properties:
Egghe L (2009) Mathematical study of h-index sequences. Information Processing & Management 45(2):288-297, doi: 10.1016/j.ipm.2008.12.002 ![]()
Guns R, Rousseau R (2009) Simulating growth of the h-index. Journal of the American Society for Information Science and Technology 60(2):410-417, doi: 10.1002/asi.20973 ![]()
Liu YX, Rousseau R (2008) Definitions of time series in citation analysis with special attention to the h-index. Journal of Informetrics 2(3):202-210, doi: 10.1016/j.joi.2008.04.003 ![]()
Rousseau R, Ye FY (2008) A proposal for a dynamic h-type index. Journal of the American Society for Information Science and Technology 59(11):1853-1855, doi: 10.1002/asi.20890 ![]()
In this work, the authors complemented the previous work to find out if power law models for a specific type of h-index time series fit real data sets. Additional comments of this work can be found in:
Burrell QL (2009) Some Comments on "A Proposal for a Dynamic h-Type Index" by Rousseau and Ye. Journal of the American Society for Information Science and Technology 60(2):418-419, doi: 10.1002/asi.20969 ![]()
Rousseau R (2007) The influence of missing publications on the Hirsch index. Journal of Informetrics 1(1):2-7, doi: 10.1016/j.joi.2006.05.001 ![]()
Rousseau has also used a continuous power law model in order to show that the influence of missing articles is largest when the total number of publications is small and non-existing when the number of publications is very large (the same conclusion is drawn for missing citations).
Deineko VG, Woeginger GJ (2009) A new family of scientific impact measures: The generalized Kosmulski-indices. Scientometrics 80(3):819-826, doi: 10.1007/s11192-009-2130-0 ![]()
This article introduces the generalized Kosmulski-indices as a new family of scientific impact measures for ranking the output of scientific researchers. As special cases, this family contains the well-known Hirsch-index h and the Kosmulski-index h(2). The main contribution is an axiomatic characterization that characterizes every generalized Kosmulski-index in terms of three axioms.
Egghe L (2009) Mathematical study of h-index sequences. Information Processing & Management 45(2):288-297, doi: 10.1016/j.ipm.2008.12.002 ![]()
This paper studies mathematical properties of h-index sequences as previously developed by Liang. The obtained results are confirmed for the h-, g- and R-sequences (forward and reverse time) of an author.
Quesada A (2009) Monotonicity and the Hirsch index. Journal of Informetrics 3(2):158-160, doi: 10.1016/j.joi.2009.01.002 ![]()
In this short contribution, the Hirsch index is characterized, when indices are allowed to be real-valued, by adding to Woeginger's monotonicity two axioms in a way related to the concept of monotonicity.
Zhang C.T. Relationship of the h-index, g-index, and e-index. Journal of the American Society for Information Science and Technology 61 (3) (2010) 625-628, doi:10.1002/asi.21274
The authors stablish a relationship among the h-, g- and e-indices when the citations for a scientist re ranked by a power law. In fact they show how the g-index can be computed from the h- and e- indices and the power parameter. The relationship of the h-, g-, and e-indices shows that the g-index contains the citation information from the h-index, the e-index, and some papers beyond the h-core.
Beirlant J., Einmahl J.H.J. Asymptotics for the Hirsch Index. Scandinavian Journal of Statistics 37 (3) (2010) 355-364, doi:10.1111/j.1467-9469.2010.00694.x
In this paper, the authors establish the asymptotic normality of the empirical h-index. The rate of convergence is non-standard: sqrt(h) / (1 + nf(h)), where f is the density of the citation distribution and n is the number of publications of a researcher.
Franceschini F., Maisano D. Analysis of the Hirsch index's operational properties. European Journal of Operational Research 203 (2) (2010) 494-504, doi:10.1016/j.ejor.2009.08.001
The authors provide a detailed analysis of the h-index, from the point of view of the indicator operational properties. It can be helpful to better understand the peculiarities and limits of h and avoid its misuse.
Henzinger M., Sunol J., Weber I. The stability of the h-index. Scientometrics 84 (2) (2010) 465-479, doi:10.1007/s11192-009-0098-7
The authors investigate if ranking according to the h-index is stable with respect to (i) different choices of citation databases, (ii) normalizing citation counts by the number of authors or by removing self-citations, (iii) small amounts of noise created by randomly removing citations or publications and (iv) small changes in the definition of the index. In their they show that although the ranking of the h-index is stable under most of these changes, it is unstable when different databases are used. Therefore, comparisons based on the h-index should only be trusted when the rankings of multiple citation databases agree.
Quesada A. Monotonicity and the Hirsch index. Journal of Informetrics 3 (2) (2009) 158-160, doi:10.1016/j.joi.2009.01.002
In this contribution, the Hirsch index is characterized, when indices are allowed to be real-valued, by adding to Woeginger's monotonicity two axioms in a way related to the concept of monotonicity.
Quesada A. More axiomatics for the Hirsch index. Scientometrics 82 (2) (2010) 413-418, doi:10.1007/s11192-009-0026-x
This contribution suggests three characterizations without adopting the monotonicity axiom.
Ye F.Y. An investigation on mathematical models of the h-index. Scientometrics 81 (2) (2009) 493-498, doi:10.1007/s11192-008-2169-6
Based on two large data samples from ISI databases, the author evaluated the Hirsch model, the Egghe-Rousseau model, and the Glänzel-Schubert model of the h-index. The results support the Glänzel-Schubert model as a better estimation of the h-index at both journal and institution levels.
Other studies that analyze the performance of different indices and their transformations
Egghe L (2008) Examples of simple transformations of the h-index: Qualitative and quantitative conclusions and consequences for other indices. Journal of Informetrics 2(2):136-148, doi: 10.1016/j.joi.2007.12.003 ![]()
Egghe L (2008) The Influence of transformations on the h-index and the g-index. Journal of the American Society for Information Science and Technology 59(8):1304-1312, doi: 10.1002/asi.20823 ![]()
In this works a comparative study about how the h-index, the g-index, the R-index and the hw -index are affected by simple transformation as doubling the production per source, doubling the number of sources, doubling the number of sources but halving their production, halving the number of sources but doubling their production (fusion of sources) and some special cases of general power law transformations is made. The author demonstrated that this kind of transformations affect in a similar way to all the h- related indices that he studied.
Egghe L (2008) The influence of merging on h-type indices. Journal of Informetrics 2(3):252-262, doi: 10.1016/j.joi.2008.06.002 ![]()
In this case the importance of merging h- type indices for different information production processes has been studied. In fact, he studies two types of information production processes mergings for the h-, g-, R- and hw - indices: one where common sources add their number of items and one where common sources get the maximum of their number of items in the two information production processes.
How to compute h-index using different Databases?
The next link presents a page describing how to compute h-index using different databases such as WoS, Scopus and Google Scholar.
In the literature there exist different studies on the use of these databases that we analyze them.
Until just a few years ago, when citation information was needed the single most comprehensive source was the ISI Citation Indexes. Although the Citation Indexes were often criticized for various reasons, there was no other source to rely on. Data from the ISI Citation Indexes and the Journal Citation Reports are routinely used by promotion committees at universities all over the world. In this paper we refer to the Web version of Citation Indexes, i.e., to the Web of Science (WOS). Recently two alternatives to the ISI Citation Indexes have become available. One of them is Scopus developed by Elsevier and the other is the freely available Google Scholar. Each of these has a different collection policy which affects both the publications covered and the number of citations to the publications (Bar-Ilan J (2008) Which h-index? - A comparison of WoS, Scopus and Google Scholar. Scientometrics 74(2):257-271, doi: dx.doi.org/10.1007/s11192-008-0216-y ![]() ). In the literature there exist different studies analyzing them:
). In the literature there exist different studies analyzing them:
Bar-Ilan J (2008) Which h-index? - A comparison of WoS, Scopus and Google Scholar. Scientometrics 74(2):257-271, doi: 10.1007/s11192-008-0216-y ![]()
This paper compares the h-indices of a list of highly-cited Israeli researchers based on citations counts retrieved from the Web of Science, Scopus and Google Scholar respectively. In several case the results obtained through Google Scholar are considerably different from the results based on the Web of Science and Scopus. Data cleansing is discussed extensively.
Jacso P (2008) The plausibility of computing the h-index of scholarly productivity and impact using reference-enhanced databases. Online Information Review 32(2):266-283, doi: 10.1108/14684520810879872 ![]()
This paper aims to provide a general overview, to be followed by a series of papers focusing on the analysis of pros and cons of the three largest, cited-reference-enhanced, multidisciplinary databases (Google Scholar, Scopus, and Web of Science) for determining the h-index. In addition, the practical aspects of determining the h-index also need scrutiny, because some content and software characteristics of reference-enhanced databases can strongly influence the h-index values.
Jacso P (2008) The pros and cons of computing the h-index using Google Scholar. Online Information Review 32(3):437-452, doi: 10.1108/14684520810889718 ![]()
The aim of this paper is to focus on Google Scholar (GS), from the perspective of calculating the h-index for individuals and journals. The paper shows that effective corroboration of the h-index and its two component indicators can be done only on persons and journals with which a researcher is intimately familiar. Corroborative tests must be done in every database for important research. Furthermore, the paper highlights the very time-consuming process of corroborating data, tracing and counting valid citations and points out GS's unscholarly and irresponsible handling of data.
Jacso P (2008) Testing the calculation of a realistic h-index in Google Scholar, Scopus, and Web of Science for F. W. Lancaster. Library Trends 56(4):784-815,![]()
This paper focuses on the practical limitations in the content and software of the databases that are used to calculate the h-index for assessing the publishing productivity and impact of researchers. To celebrate F.W. Lancaster's biological age of seventy-five, and "scientific age" of forty-five, this paper discusses the related features of Google Scholar, Scopus, and Web of Science (WoS), and demonstrates in the latter how a much more realistic and fair h-index can be computed for F.W. Lancaster than the one produced automatically. Browsing and searching the cited reference index of the 1945-2007 edition of WoS, which in his estimate has over a hundred million "orphan references" that have no counterpart master records to be attached to, and "stray references" that cite papers which do have master records but cannot be identified by the matching algorithm because of errors of omission and commission in the references of the citing works, can bring up hundreds of additional cited references given to works of an accomplished author but are ignored in the automatic process of calculating the h-index. The partially manual process doubled the h-index value for F.W. Lancaster from 13 to 26, which is a much more realistic value for an information scientist and professor of his stature.
Meho LI, Rogers Y (2008) Citation counting, citation ranking, and h-index of human-computer interaction researchers: A comparison of Scopus and Web of Science. Journal of the American Society for Information Science and Technology 59(11):1711-1726, doi: 10.1002/asi.20874 ![]()
This study examines the differences between Scopus and Web of Science in the citation counting, citation ranking, and h-index of 22 top human-computer interaction (HCI) researchers from EQUATOR, a large British Interdisciplinary Research Collaboration project. Results indicate that Scopus provides significantly more coverage of HCI literature than Web of Science, primarily due to coverage of relevant ACM and IEEE peer-reviewed conference proceedings. No significant differences exist between the two databases if citations in journals only are compared. Although broader coverage of the literature does not significantly alter the relative citation ranking of individual researchers, Scopus helps distinguish between the researchers in a more nuanced fashion than Web of Science in both citation counting and h-index. Scopus also generates significantly different maps of citation networks of individual scholars than those generated by Web of Science. The study also presents a comparison of h-index scores based on Google Scholar with those based on the union of Scopus and Web of Science. The study concludes that Scopus can be used as a sole data source for citation-based research and evaluation in HCI, especially when citations in conference proceedings are sought, and that researchers should manually calculate h scores instead of relying on system calculations.
Meho LI, Yang K (2007) Impact of data sources on citation counts and rankings of LIS faculty: Web of science versus scopus and google scholar. Journal of the American Society for Information Science and Technology 58(13):2105-2125, doi: 10.1002/asi.20677 ![]()
The Institute for Scientific Information's (ISI, now Thomson Scientific, Philadelphia, PA) citation databases have been used for decades as a starting point and often as the only tools for locating citations and/or conducting citation analyses. The ISI databases (or Web of Science [WoS]), however, may no longer be sufficient because new databases and tools that allow citation searching are now available. Using citations to the work of 25 library and information science (LIS) faculty members as a case study, the authors examine the effects of using Scopus and Google Scholar (GS) on the citation counts and rankings of scholars as measured by WoS. Overall, more than 10,000 citing and purportedly citing documents were examined. Results show that Scopus significantly alters the relative ranking of those scholars that appear in the middle of the rankings and that GS stands out in its coverage of conference proceedings as well as international, non-English language journals. The use of Scopus and GS, in addition to WoS, helps reveal a more accurate and comprehensive picture of the scholarly impact of authors. The WoS data took about 100 hours of collecting and processing time, Scopus consumed 200 hours, and GS a grueling 3,000 hours.
Bornmann L, Marx W, Schier H, Rahm E, Thor A, Daniel HD (2009) Convergent validity of bibliometric Google Scholar data in the field of chemistry-Citation counts for papers that were accepted by Angewandte Chemie International Edition or rejected but published elsewhere, using Google Scholar, Science Citation Index, Scopus, and Chemical Abstracts. Journal of Informetrics 3(1):27-35, doi: 10.1016/j.joi.2008.11.001 ![]()
The authors compare the citations obtained from Google Scholar vs the citations obtained by three fee-based databases (Science Citation Index, Scopus and Chemical Abstracts). The analyses using citations returned by the three fee-based databases show very similar results. On the other hand, the results of the analysis using GS citation data differed greatly from the findings using citations from the fee-based databases. The study therefore supports, on the one hand, the convergent validity of citation analyses based on data from the fee-based databases and, on the other hand, the lack of convergent validity of the citation analysis based on the GS data.
Armbruster C. Whose metrics? Citation, usage and access metrics as scholarly information service. Learned Publishing 23 (1) (2010) 33-38, doi: 10.1087/20100107
The authors analize what kind of metric information services would serve scholars to better construct databases that deliver services of value to them.
Bar-Ilan J. Web of Science with the Conference Proceedings Citation Indexes: the case of computer science. Scientometrics 83 (3) (2010) 809-824, doi: 10.1007/s11192-009-0145-4
The author discusses how the inclusion of Conference Proceedings Citation Indexes for Science and for the Social Sciences and Humanities in the ISI Web of Science influence on the citation based indices for highly cited scientists. As Computer Science is a field where proceedings are a major publication venue, it is shown that the most cited publications are journal papers but a large amount of citations come from proceeding papers, thus incresing citation based indices. In addition the author discusses how some publications may be double counted when a work is published in both a conference and a journal.
Derrick G.E., Sturk H., Haynes A.S., Chapman S., Hall W.D. A cautionary bibliometric tale of two cities. Scientometrics 84 (2) (2010) 317-320, doi: 10.1007/s11192-009-0118-7
The authors address the problem of different suscription policies to databases, particularly to Wob of Science and Web of Knowledge. In fact, the authors compare simultaneous search returns at two sites to demonstrate discrepancies that can occur as a result of differences in institutional subscriptions to those databases. Moreover, such discrepancies may have significant implications for the reliability of bibliometric research in general, but also for the calculation of individual and group indices used for promotion and funding decisions.
Franceschet M. A comparison of bibliometric indicators for computer science scholars and journals on Web of Science and Google Scholar. Scientometrics 83 (1) (2010) 243-258, doi: 10.1007/s11192-009-0021-2
In this contribution a case study for computer science scholars and journals evaluated on Web of Science and Google Scholar databases is provided. The study concludes that Google scholar computes significantly higher indicators’ scores than Web of Science. Nevertheless, citation-based rankings of both scholars and journals do not significantly change when compiled on the two data sources, while rankings based on the h index show a moderate degree of variation.
Mikki S. Comparing Google Scholar and ISI Web of Science for Earth Sciences. Scientometrics 82 (2) (2010) 321-331, doi: 10.1007/s11192-009-0038-6
The authors compare search results from Google Scholar with ISI WoS in order to measure the degree to which the first can compete with bibliographical databases. For earth science literature 85% of documents indexed by ISI WoS were recalled by Google Scholar. The rank of records displayed in Google Scholar and ISI WoS, is compared by means of Spearman’s footrule. For impact measures the h-index is investigated. Similarities in measures were significant for the two sources.
Mingers J., Lipitakis E.A.E.C.G. Counting the citations: a comparison of Web of Science and Google Scholar in the field of business and management. Scientometrics 85 (2) (2010) 613-625, doi: 10.1007/s11192-010-0270-0
Due to the less extensive coverage in social sciences, ISI Web of Science is compared with Google Scholar for two different datasets of 4600 publications from three UK Business Schools. The results show that Web of Science is indeed poor in the area of management and that Google Scholar, whilst somewhat unreliable, has a much better coverage. The results suggest thant Web of Science should not be used for measuring research impact in management.
Kousha K., Thelwall M. Rezaie S. Using the Web for research evaluation: The Integrated Online Impact indicator. Journal of Informetrics 4 (1) (2009) 124-135, doi: 10.1016/j.joi.2009.10.003
This paper presents a combined Integrated Online Impact indicator. It is based in five online sources of citation data: Google Scholar, Google Books, Google Blogs, Power Point presentations and course reading lists. The results from a set of research articles published in the Journal of the American Society for Information Science & Technology (JASIST) and Scientometrics in 2003 are compared with the citation counts obtained by WoS and Scopus. The results show that the mean and median IOI was nearly twice as high as both WoS and Scopus, confirming that online citations are sufficiently numerous to be useful for the impact assessment of research. The authors also found significant correlations between conventional and online impact indicators, confirming that both assess something similar in scholarly communication.
On the use of h- related indices to assess groups of individuals, institutions and journals
h- and related indices have been used to evaluate not only individual researchers but also higher level research institutions. In addition to the specific indices for the evaluation of the scientific production at different levels here we present some studies that use the h-index and derived ones to asses the scientific production of groups of individuals, institutions and journals.
Bornmann L, Marx W, Schier H (2009) Hirsch-type index values for organic chemistry journals: a comparison of new metrics with the Journal Impact Factor. European Journal of Organic Chemistry 10:1471-1476, doi: 10.1002/ejoc.200801243 ![]()
In this paper a comparison of some of the well known h-index variants is made. The aim of this analysis is to determine empirically the extent to which the usage of the h index and its variants for measuring the performance of journals results in an incremental contribution against the Journal Impact Factor. Particularly the authors used 20 organic chemistry journals for the study. This idea is also discussed in:
Bornmann L, Daniel HD (2009) The state of h index research. Is the h index the ideal way to measure research performance?. EMBO Reports 10(1):2-6, doi: 10.1038/embor.2008.233 ![]()
Liu YX, Rao IKR, Rousseau R (2009) Empirical series of journal h-indices: The JCR category Horticulture as a case study. Scientometrics 80(1):59-74, doi: 10.1007/s11192-007-2026-z ![]()
In this work two types of series of h-indices for journals published in the field of Horticulture during the period 1998–2007 are calculated. The authors proved that the journals (in Horticulture) do not exhibit a linear increase in h-index as argued by Hirsch in the case of life-time achievements of scientists. They also studied how the relative visibility of a journal and its change over time, based on h-indices of journals.
Arencibia-Jorge R, Barrios-Almaguer I, Fernandez-Hernandez S, Carvajal-Espino R (2008) Applying successive H indices in the institutional evaluation: A case study. Journal of the American Society for Information Science and Technology 59(1):155-157, doi: 10.1002/asi.20729 ![]()
Following a previous idea by Schubert, the authors apply the idea of successive h-indices to perform a case study of the scientific production of different institutions using a researcher-department-institution hierarchy as levels of aggregation. They improve their study by using additional h- related indices as complementary indicators. That idea is further complemented in:
Arencibia-Jorge R (2009) New indicators of institutional scientific performance based on citation analysis: the successive H indices. Revista Española de Documentacion Cientifica 32(3):101-106, doi: 10.3989/redc.2009.3.692
Arencibia-Jorge R, Rousseau R (2009) Influence of individual researchers' visibility on institutional impact: an example of Prathap's approach to successive h-indices. Scientometrics 79(3):507-516, doi: 10.1007/s11192-007-2025-0 ![]()
Rodriguez-Navarro A (2009) Sound Research, Unimportant Discoveries: Research, Universities, and Formal Evaluation of Research in Spain. Journal of the American Society for Information Science and Technology 60(9):1845-1858, doi: 10.1002/asi.21104 ![]()
In this work the author tries to relate the growth of the production of Spanish researches with the growth of h-related indices, concluding that both measures do not grow at the same speed.
Riikonen P, Vihinen M (2008) National research contributions: A case study on Finnish biomedical research. Scientometrics. 77(2):207-222, doi:10.1007/s11192-007-1962-y ![]()
Riikonen and Vihinen suggest that analyses of the scientific contribution of persons, disciplines, or nations should be based on actual publication and citation counts rather than on derived information like impact factors.
Egghe L, Liang LM, Rousseau R (2009) A Relation Between h-Index and Impact Factor in the Power-Law Model. Journal of the American Society for Information Science and Technology 60(11):2362-2365, doi:10.1002/asi.21144 ![]()
Using a power-law model, the two best-known topics in citation analysis, namely the impact factor and the Hirsch index, are unified into one relation (not a function). The authors validate of their model (in a qualitative way) using real data.
Jacso P (2009) The h-index for countries in Web of Science and Scopus. Online Information Review 33(4):831-837, doi:10.1108/14684520910985756 ![]()
In this paper the h-index is used to rank 10 Ibero-American countries of South America using data from both Web of Science and Scopus. Although the data obtained by both databses is quite different the obtained rank correlations is very high.
Schubert A, Korn A, Telcs A (2009) Hirsch-type indices for characterizing networks. Scientometrics 78(2):375-382, doi:10.1007/s11192-008-2218-1 ![]()
In this contribution, the role of the h-type indices as to characterize networks and network elements is studied. The authors suggest that this kind of indices are not only useful for bibliometric pourposes but in an almost unlimited range of assesement applications.
Sypsa V, Hatzakis A (2009) Assessing the impact of biomedical research in academic institutions of disparate sizes. BMC Medical Research Methodology 9:33, doi:10.1186/1471-2288-9-33 ![]()
The authors propose a new complementary measure to the h-index when comparing the research output of institutions of disparate sizes. The measure has a conceptual interpretation and, with the data provided in the paper, can be computed for the total research output as well as for field-specific publication sets of institutions in biomedicine.
Moussa S, Touzani M (2010) Ranking marketing journals using the Google Scholar-based hg-index. Journal of Informetrics 4(1):107-117, doi:10.1016/j.joi.2009.10.001 ![]()
This paper provides a ranking of 69 marketing journals using a new Hirsch-type index, the hg-index which is the geometric mean of hg. The applicability of this index is tested on data retrieved from Google Scholar on marketing journal articles published between 2003 and 2007. The authors investigate the relationship between the hg-ranking, ranking implied by Thomson Reuters' Journal Impact Factor for 2008, and rankings in previous citation-based studies of marketing journals. They also test two models of consumption of marketing journals that take into account measures of citing (based on the hg-index), prestige, and reading preference.
Empirical studies that use h- and related indices
In the literature a yet growing number of empirical studies that use the h- and related indices can be found. In the following we show some of those studies to examplify the broad number of areas in which these indices are gaining attraction:
Economical Geography
Bodman A.R. Measuring the influentialness of economic geographers during the 'great half century': an approach using the h index. Journal of Economic Geography 10 (1) (2010) 141-156, doi:10.1093/jeg/lbp061
Nanotechnology
Guan J.C., Wang G.B. A comparative study of research performance in nanotechnology for China's inventor-authors and their non-inventing peers. Scientometrics 82 (2) (2010) 331-343, doi:10.1007/s11192-009-0140-9
Social Sciences
Haddow G., Genoni P. Citation analysis and peer ranking of Australian social science journals. Scientometrics 85 (2) (2010) 471-487, doi:10.1007/s11192-010-0198-4
Psychology
Haslam N., Laham S.M. Quality, quantity, and impact in academic publication. European Journal of Social Psychology 40 (2) (2010) 216-220, doi:10.1002/ejsp.727
Psychiatry
Hunt G.E., Cleary M., Walter G. Psychiatry and the Hirsch h-index: The Relationship Between Journal Impact Factors and Accrued Citations. Harvard Review of Psychiatry 18 (4) (2010) 207-219, doi:10.3109/10673229.2010.493742
Neurosurgery
Lee J., Kraus K.L., Couldwell W.T. Use of the h index in neurosurgery Clinical article. Journal of Neurosurgery 111 (2) (2009) 387-392, doi:10.3171/2008.10.JNS08978
Horticulture
Liu Y.X., Rao I.K.R. Empirical series of journal h-indices: The JCR category Horticulture as a case study. Scientometrics 80 (1) (2009) 59-74, doi:10.1007/s11192-007-2026-z
Radiology
Rad A.E., Brinjikji W., Cloft H.J., Kallmes D.F. The H-Index in Academic Radiology. Academic Radiology 17 (7) (2010) 817-821, doi:10.1016/j.acra.2010.03.011
Manufacturing and Quality Engineering
Franceschini F., Maisano D. The Hirsch Index in Manufacturing and Quality Engineering. Quality and Reliability Engineering International 25 (8) (2009) 987-995, doi:10.1002/qre.1016
Astronomy
Sierra-Flores M.M., Guzman M.V., Raga A.C., Perez I. The productivity of Mexican astronomers in the field of outflows from young stars. Scientometrics 81 (3) (2009) 765-777, doi:10.1007/s11192-008-2264-8
WEB sites or journal special issues devoted to h-index
- Ronald Rousseau's Homepage: articles related to the h-index and h-type indices.
- Journal of Informetrics. Special Issue: The Hirsch Index. Volume 1, Issue 3, pages 179-213 (5 papers), July 2007.
- Wikipedia: h-index.
- A MATLAB script to compute the h-index.
- Publish or Perish calculates various statistics, including the h-index and the g-index using Google Scholar data.
- H index for Journals and Countries.
- Scientometrics.
- Journal of Informetrics.
- Journal of the American Society for Information Science and Technology (JASIST).
- El Profesional de la Información.
Bibliography compilation about the h-index and related areas
We have performed a bibliography compilation of journal papers on h-index and related areas. It is maintained by F.J. Cabrerizo.
If you would like to include or correct any of the references on this page, please contact the maintainer in his e-mail address: cabrerizo@issi.uned.es
