Evolutionary Algorithms and other Metaheuristics for Continuous Optimization Problems

This Website is devoted to a Evolutionary Algorithms and other Metaheuristics for Continuous Optimization Problems. It is maintained by M. Lozano, D. Molina, C. García-Martínez, F. Herrera following the next summary:

  1. Introduction
  2. Pioneer and Outstanding Contributions
  3. Books and Special Issues
  4. Special Sesions and Workshops
  5. Large Scale Optimization Problems
  6. Complementary Material: SOCO Special Issue on Large Scale Continuous Optimization Problems
  7. Software
  8. Slides
  9. Test Functions and Results
  10. Statistical Test Based Methodologies for Algorithm Comparisons
  11. Future Events

Introduction: Evolutionary Algorithms, Swarm Intelligence, and other Metaheuristics for Continuous Optimization Problems

Many real-world problems may be formulated as optimization problems of parameters with variables in continuous domains (continuous optimization problems). Over the past few years, the field of global optimization has been very active, producing different kinds of deterministic and stochastic algorithms for optimization in the continuous domain. Among the stochastic approaches, evolutionary algorithms (EAs) offer a number of exclusive advantages: robust and reliable performance, global search capability, little or no information requirement, etc. These characteristics of EAs, as well as other supplementary benefits such as ease of implementation, parallelism, no requirement for a differentiable or continuous objective function, etc., make it an attractive choice. Consequently, there have been many studies related to real-parameter optimization using EAs, resulting in many variants such as:

  • Real-coded Genetic Algorithms (Herrera F, Lozano M, Verdegay JL. Tackling real-coded genetic algorithms: Operators and tools for behavioural analysis. Artificial Intelligence Review 12(4), 265-319, 1998 doi: 10.1023/A:1006504901164).
  • Evolution Strategies (Beyer, H.-G., Schwefel, H.-P. Evolution strategies. Natural Computing 1, 3–52, 2002 doi: 10.1023/A:1015059928466).
  • Evolutionary Programming (Lee, C.-Y., Yao, X. Evolutionary programming using mutations based on the Levy probability distribution. IEEE Transactions on Evolutionary Computation 8 (1), 1–13, 2004 doi: 10.1109/TEVC.2003.816583).
  • Real-coded Memetic Algorithms (Lozano, M., Herrera, F., Krasnogor, N., Molina, D. Real-coded memetic algorithms with crossover hill-climbing. Evolutionary Computation Journal 12 (3), 273–302, 2004 doi: 10.1162/1063656041774983).
  • Differential Evolution (Storn, R., Price, K. Differential evolution – a simple and efficient heuristic for global optimization over continuous spaces. Journal of Global Optimization 11 (4), 341–359, 1997 doi: 10.1023/A:1008202821328 ).

A common characteristic of these EAs is that they evolve chromosomes that are vectors of floating point numbers, directly representing problem solutions. Hence, they may be called real-coded EAs.

Figures 1-3 show the evolution of citations in each year for three relevant publications proposing different real-coded EA models. Clearly, we may observe that these algorithms have aroused increasing interest over the last few years.

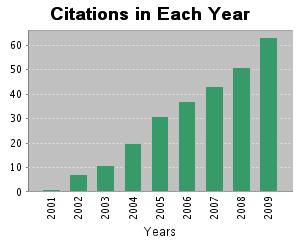
Fig. 1. Hansen N, Ostermeier A. Completely derandomized self-adaptation in evolution strategies. EVOLUTIONARY COMPUTATION 9(2), 159-195, 2001 doi: 10.1162/106365601750190398. Sum of the Times Cited: 263 (October 2009)

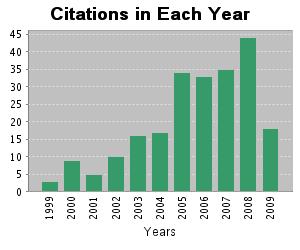
Fig. 2. Herrera F, Lozano M, Verdegay JL. Tackling real-coded genetic algorithms: Operators and tools for behavioural analysis. ARTIFICIAL INTELLIGENCE REVIEW 12(4) , 265-319, 1998 doi: 10.1023/A:1006504901164. Sum of the Times Cited: 224 (October 2009)

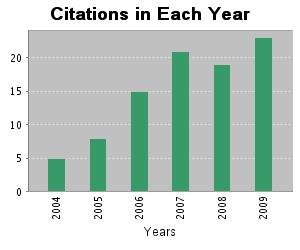
Fig. 3. Deb K, Anand A, Joshi D. A computationally efficient evolutionary algorithm for real-parameter optimization. EVOLUTIONARY COMPUTATION 10(4), 371-395, 2002 doi: 10.1162/106365602760972767. Sum of the Times Cited: 91 (October 2009)

We can also find interesting Swarm Intelligence (SI) based continuous optimization approaches:

  • Ant Colony Optimization Algorithms (Socha, K. & Dorigo, M. Ant colony optimization for continuous domains. European Journal of Operational Research 18(3), 2008, 1155-1173 doi: 10.1016/j.ejor.2006.06.046).
  • Particle Swarm Optimisation (Kennedy, J., Eberhart, R.C. Particle swarm optimization. In: Proc. of the IEEE International Conference on Neural Networks, Piscataway, New Jersey, pp. 1942–1948, 1995 doi: 10.1109/ICNN.1995.488968).
  • Artificial Bee Colony Optimization (D. Karaboga, B. Basturk. A powerful and efficient algorithm for numerical function optimization: artificial bee colony (ABC) algorithm. Journal of Global Optimization, 39, 2007, 459-471 doi: 10.1007/s10898-007-9149-x).
  • Bacterial Foraging Optimization (Y. Lui, K.M. Passino. Biomimicry of Social Foraging Bacteria for Distributed Optimization: Models, Principles, and Emergent Behaviors. Journal of Optimization Theory and Applications 115:3, 2002, 603-628 doi:10.1023/A:1021207331209).

Finally, other Metaheuristic models have been considered to deal with continuous optimization problems:

  • Estimation of Distribution Algorithms (Chang Wook Ahn, R. S. Ramakrishna. On the scalability of real-coded bayesian optimization algorithm. IEEE Transaction of Evolutionary Computation 12(3), 2008, 307-322 doi: 10.1109/TEVC.2007.902856).
  • Simulated Annealing (Vanderbilt, D., Louie, S.G. A monte-carlo simulated annealing approach to optimization over continuous-variables. Journal of Computational Physics 56(2), 1984, 259-271 doi: 10.1016/0021-9991(84)90095-0).
  • Variable Neighborhood Search (N. Mladenovic, M. Drazic, V. Kovacevic-Vujcic, M. Cangalovic. General variable neighborhood search for the continuous optimization. European Journal of Operational Research 191, 2008, 753–770 doi: 10.1016/j.ejor.2006.12.064).
  • Tabu Search (Glover, F. Tabu search for nonlinear and parametric optimization (with links to genetic algorithms). Discrete Applied Mathematics 49(1-3), 1994, 231-255 doi: 10.1016/0166-218X(94)90211-9).
  • Scatter Search (F. Herrera, M. Lozano, D. Molina. Continuous scatter search: an analysis of the integration of some combination methods and improvement strategies. European Journal of Operational Research 169:2, 2005, 450-476 doi: 10.1016/j.ejor.2004.08.009).
  • Continuous GRASP (M.J. Hirsch, P.M. Pardalos, M.G.C. Resende. Solving systems of nonlinear equations with continuous GRASP. Nonlinear Analysis: Real World Applications 10, 2009, 2000–2006 doi: 10.1016/j.nonrwa.2008.03.006).
  • Central Force Optimization (R.A. Formato, Central Force Optimization: A New Metaheuristic with Applications in Applied Electromagnetics. Progress In Electromagnetics Research 77, 2007, 425-491 doi: 10.2528/PIER07082403).

Pioneer and Outstanding Contributions

Next, we list some of the most outstanding contributions of EAs and other metaheuristics for continuous optimization problems:

Real-coded Genetic Algorithms

  • Wright, A. (1991). Genetic Algorithms for Real Parameter Optimization. FOGA 1, 205-218.
  • Goldberg D.E. (1991). Real-Coded Genetic Algorithms, Virtual Alphabets, and Blocking. Complex Systems 5, 139-167.
  • Eshelman L.J., Schaffer J.D. (1993). Real-Coded Genetic Algorithms and Interval-Schemata. FOGA 2, 187-202.
  • F. Herrera, M. Lozano, J.L. Verdegay (1998). Tackling real-coded genetic algorithms: operators and tools for the behavioural analysis. Artificial Intelligence Reviews 12(4): 265-319 doi: 10.1023/A:1006504901164.
  • Deb, K., Anand, A., Joshi, D. (2002). A computationally efficient evolutionary algorithm for real-parameter evolution. Evolutionary Computation 10(4): 371-395 doi: 10.1162/106365602760972767.
  • Herrera, F., Lozano, M., Sánchez, A.M. (2003). A Taxonomy for the Crossover Operator for Real-Coded Genetic Algorithms: An Experimental Study. International Journal of Intelligent Systems 18: 309-338 doi: 10.1002/int.10091.

Real-coded Memetic Algorithms

  • Hart, W. E. (1994). Adaptive Global Optimization with Local Search. Ph.D. Thesis, University of California, San Diego, California.
  •  
  • Renders J. M. and Flasse, S. P. (1996). Hybrid methods using genetic algorithms for global optimization. IEEE Transactions on Systems, Man, and Cybernetics, 26(2): 243–258 doi: 10.1109/3477.485836.
  • Ong, Y-S. and Keane, A. J. (2004). Meta-Lamarckian learning in memetic algorithms. IEEE Transactions on Evolutionary Computation, 4(2):99–110 doi: 10.1109/TEVC.2003.819944.
  • Lozano, M., Herrera, F., Krasnogor, N., and Molina, D. (2004). Real-coded memetic algorithms with crossover hill-climbing. Evolutionary Computation, 12(3): 273–302 doi: 10.1162/1063656041774983.

Evolution Strategies

  • Hansen, N., Ostermeier, A. (2001). Completely derandomized self-adaptation in evolution strategies. Evolutionary Computation, 9(2): 159-195 doi: http://dx.doi.org/10.1162/106365601750190398.
  • Auger, A., Hansen, N. (2005). A restart CMA evolution strategy with increasing population size. In Proc. of the 2005 IEEE Congress on Evolutionary Computation, pages 1769-1776 doi: 10.1109/CEC.2005.1554902.

Differential Evolution

  • Storn, R., Price, K. (1997). Differential evolution – a simple and efficient heuristic for global optimization over continuous spaces. Journal of Global Optimization 11 (4), 341–359 doi: 10.1023/A:1008202821328.

Particle Swarm Optimization

  • Kennedy, J., Eberhart, R. (1995). Particle swarm optimization. Proc. of the IEEE International Conference on Neural Networks, Piscataway, New Jersey, pp. 1942–1948, 1995 doi: 10.1109/ICNN.1995.488968.
  • Kennedy, J., Eberhart R.C., Shi Yuhui (2001). Swarm Intelligence. The Morgan Kaufmann series in Evolutionary Computation. Morgan Kauffmann. ISBN: 1558605959, 2001.

Ant Colony Optimization

  • Bilchev, G. & Parmee, I. C. (1995). The ant colony metaphor for searching continuous design spaces. In T. C. Fogarty (Ed.), Evolutionary Computing, AISB Workshop, Lecture Notes in Computer Science 993 (pp. 25–39), Springer doi: 10.1007/3-540-60469-3_22.
  • Socha, K. & Dorigo,M. (2008). Ant colony optimization for continuous domains. European Journal of Operational Research 185(3), 1155-1173 doi: 10.1016/j.ejor.2006.06.046.

Estimation of Distribution Algorithms

  • Chang Wook Ahn, Ramakrishna, R.S. (2008). On the scalability of real-coded bayesian optimization algorithm. IEEE Transaction of Evolutionary Computation 12(3), 307-322 doi: 10.1109/TEVC.2007.902856.

Variable Neighbourhood Search

  • Mladenovic, N., Drazic, M., Kovacevic-Vujcic, V., Cangalovic, M. (2008). General variable neighborhood search for the continuous optimization. Operational Research 191, 753–770 doi: 10.1016/j.ejor.2006.12.064.

Tabu Search

  • Glover, F. (1994). Tabu search for nonlinear and parametric optimization (with links to genetic algorithms). Discrete Applied Mathematics 49(1-3), 231-255 doi: 10.1016/0166-218X(94)90211-9.
  • Chelouah R, Siarry P. (2000). Tabu search applied to global optimization. European Journal of Operational Research 123(2), 256-270 doi: 10.1016/S0377-2217(99)00255-6.

Simulated Annealing

  • Vanderbilt, D., Louie, S.G. (1984). A monte-carlo simulated annealing approach to optimization over continuous-variables. Journal of Computational Physics 56(2), 259-271 doi: 10.1016/0021-9991(84)90095-0.
  • Pedamallu, C.S., Ozdamar, L.(2008). Investigating a hybrid simulated annealing and local search algorithm for constrained optimization. European Journal of Operational Research 185, 1230-1245 doi: 10.1016/j.ejor.2006.06.050.

Scatter Search

  • M. Laguna, R. Martí (2005). Experimental Testing of Advanced Scatter Search Designs for Global Optimization of Multimodal Functions. Journal of Global Optimization 33, 235-255 doi: 10.1007/s10898-004-1936-z.
  • Herrera, F., Lozano, M., Molina, D. (2005). Continuous scatter search: an analysis of the integration of some combination methods and improvement strategies. European Journal of Operational Research 169:2, 450-476 doi: 10.1016/j.ejor.2004.08.009.

Greedy Randomized Adaptive Search Procedures

  • Hirsch, M.J., Pardalos, P.M., Resende, M.G.C. (2009). Solving systems of nonlinear equations with continuous GRASP. Nonlinear Analysis: Real World Applications 10, 2000-2006 doi: 10.1016/j.nonrwa.2008.03.006.

Artificial Bee Colony Optimization

  • Karaboga, D., Basturk, B. (2007). A powerful and efficient algorithm for numerical function optimization: artificial bee colony (ABC) algorithm. Journal of Global Optimization, 39, 459-471 doi: 10.1007/s10898-007-9149-x.
  • Karaboga, D., Basturk, B. (2008). On the performance of artificial bee colony (ABC) algorithm. Applied Soft Computing, 8, 687-697 doi:10.1016/j.asoc.2007.05.007.

Bacterial Foraging Optimization

  • Lui, Y., Passino, K.M. (2002). Biomimicry of Social Foraging Bacteria for Distributed Optimization: Models, Principles, and Emergent Behaviors. Journal of Optimization Theory and Applications 115:3, 603-628 doi:10.1023/A:1021207331209.
  • Passino, K.M. (2002). Biomimicry of Bacterial Foraging for Distributed Optimization and Control. IEEE Control System Magazine 52, 52-67.
  • Dasgupta, S., Das, S., Abraham, A. (2009). Adaptive Computational Chemotaxis in Bacterial Foraging Optimization: An Analysis. IEEE Transactions on Evolutionary Computation 13:4, 919-941 doi:10.1109/TEVC.2009.2021982.

Central Force Optimization

Variable Mesh Optimization

  • Puris, A., Bello, R., Molina, D., Herrera, F. (2011). Variable mesh optimization for continuous optimization problems. Soft Computing, In press, 2011 doi: 10.1007/s00500-011-0753-9.

Books and Special Issues

Books

Michalewicz, Z. (1992). Genetic Algorithms + Data Structures = Evolution Programs. Springer-Verlag, New York.
Schwefel, H.-P. (1995). Evolution and Optimum Seeking. Wiley, New York.
Kennedy, J., Eberhart, R.C. (2001). Swarm Intelligence. Morgan Kauffmann.
Price, K.V., Storn, R.M., Lampinen, J.A. (2005). Differential Evolution: A Practical Approach to Global Optimization. Springer-Verlag.

Special Issues

F. Herrera, M. Lozano (Eds.) (2005). Special Issue on Real Coded Genetic Algorithms: Foundations, Models and Operators. Soft Computing 9:4. Table of contents
Z. Michalewicz and P. Siarry (2008). Special Issue on adaptation of discrete metaheuristics to continuous optimization. European Journal of Operational Research 185, 1060–1061. Table of contents

Special Sessions and Workshops: Problem definitions and contributions (pdf files)

Special Session on Real-Parameter Optimization. 2005 IEEE CEC, Edinburgh, UK, Sept 2-5. 2005. Organizers: K. Deb and P.N. Suganthan.

Website of the special sesion

Problem Definitions and Evaluation Criteria

Contributions

Results of the presented algorithms (Excel file)

Analysis of results by N. Hansen

S. Garcia, D. Molina, M. Lozano, F. Herrera, A study on the use of non-parametric tests for analyzing the evolutionary algorithms' behaviour: a case study on the CEC'2005 Special Session on Real Parameter Optimization. Journal of Heuristics 15 (2009) 617-644.

Special Session & Competition on Large Scale Global Optimization. 2008 IEEE CEC, Hong Kong, June 1-6, 2008. Organizers: Ke Tang, Xin Yao, P.N. Suganthan, and Cara MacNish.

Website of the special sesion

Problem Definitions and Evaluation Criteria

Contributions

Results of the presented algorithms (Excel file)

Analysis of results by K. Tang

Metaheurísticas, Algoritmos Evolutivos y Bioinspirados para Problemas de Optimización Continua. VI Congreso Español de Metaheurísticas, Algoritmos Evolutivos y Bioinspirados. Málaga - February 2009. Organizers: Francisco Herrera, Manuel Lozano, Ana María Sánchez, Daniel Molina.

Contributions

Results of the presented algorithms (Excel file)

Presentation (M. Lozano)

Analysis of results by F. Herrera

A GECCO 2009 Workshop for Real-Parameter Optimization: Black-Box Optimization Benchmarking (BBOB) 2009. GECCO 2009, Montreal, Canada, July 8-12 2009. Organizers: Anne Auger, Hans-Georg Beyer, Nikolaus Hansen, Steffen Finck, Raymond Ros, Marc Schoenauer, and Darrell Whitley.

Website of the Workshop

Problem Definitions and Evaluation Criteria

Contributions

Final analysis of results on BBOB-2009 (by N. Hansen, A. Auger, R. Ros, S. Finck and P. Posík)

Analysis of results on the noiseless functions by The BBOBies

Analysis of results on the noisy functions by The BBOBies

all the results (from the Website of the Workshop)

A GECCO 2010 Workshop for Real-Parameter Optimization: Black-Box Optimization Benchmarking (BBOB) 2010. GECCO 2010, Portland, USA, July 7-11 2010. Organizers: Anne Auger, Hans-Georg Beyer, Steffen Finck, Nikolaus Hansen, Petr Posik, Raymond Ros.

Website of the Workshop

Problem Definitions and Evaluation Criteria

Contributions

Comparison table of the results on noisyless functions

Comparison table of the results on noisy functions

all the results (from the Website of the Workshop)

Workshop for Evolutionary Algorithms and other Metaheuristics for Continuous Optimization Problems - A Scalability Test. ISDA'09, Pisa, Italy, November 30 - December 2, 2009. Organizers: Francisco Herrera and Manuel Lozano.

Call for papers

Contributions

Results of the presented algorithms (Excel file)

Special Session on Large Scale Global Optimization CEC'2010, Barcelona, Spain, July 18 - 23, 2010. Organizers: Ke Tang, Xiaodong Li, P.N. Suganthan.

Website of the special sesion

Problem Definitions and Evaluation Criteria

Contributions

Results of the presented algorithms (Excel file)

Analysis of results by K. Tang

Special Track: Competition: Testing Evolutionary Algorithms on Real-world Numerical Optimization Problems CEC'2011, New Orleans, USA, Jun 5 - 8, 2011. Organizer: P.N. Suganthan.

Website of the special sesion

Problem Definitions and Evaluation Criteria

Contributions

Results of the presented algorithms (Excel file)

Large Scale Optimization Problems

In the past two decades, different kinds of nature-inspired optimization algorithms that have been designed and applied to solve optimization problems. Although these approaches have shown excellent search abilities when applying to some 30-100 dimensional problems, many of them suffer from the "curse of dimensionality", which implies that their performance deteriorates quickly as the dimensionality of search space increases. The reasons appear to be two-fold. First, complexity of the problem usually increases with the size of problem, and a previously successful search strategy may no longer be capable of finding the optimal solution. Second, the solution space of the problem increases exponentially with the problem size, and a more efficient search strategy is required to explore all the promising regions in a given time budget.

Nowadays, the ability to tackle high-dimensional problems is crucial to many real problems (bio-computing, data mining, etc.), arising high-dimensional optimization problems as a very interesting field of research. Thus, the ability of being scalable for high-dimensional problems becomes an essential requirement for modern optimization algorithm approaches. Thus, scaling EAs to large size problems have attracted much interest, including both theoretical and practical studies. However, existing work on this topic are often limited to the test problems used in individual studies, and until recently a systematic evaluation platform was not available in the literature for comparing the scalability of different EAs.

Fortunately, in recent years, researchers in this field have noticed the need of a standard test suite specially designed for large scale problems, proposing in several workshops test suites for large scale problems.

Special Workshops for Large Scale Optimizations

  • Special Session & Competition on Large Scale Global Optimization at CEC 2008.

  • Workshop for Evolutionary Algorithms and other Metaheuristics for Continuous Optimization Problems - A Scalability Test at ISDA'09.

  • Special Session & Competition on Large Scale Global Optimization at CEC 2010.

In both cases, a set of scalable function optimization problems was provided to assess the performance of different Evolutionary Algorithms and Meta-Heuristics models specifically proposed for tackling these problems.

 

Special Issues for Large Scale Optimization

  • Special Issue of Soft Computing: A Fusion of Foundations, Methodologies and Applications on Scalability of Evolutionary Algorithms and other Metaheuristics for Large Scale Continuous Optimization Problems

This Special Issue uses as test suite an extension of presented for ISDA'2009 Workshop. (Description of the 19 functions)

  1. F1-F6 of the CEC'2008 test suite. (Description) (Source code).
  2. Schwefel's Problem 2.22 (F7), Schwefel's Problem 1.2 (F8), Extended f10 (F9), Bohachevsky (F10), and Schaffer (F11). (Description) (Source code).
  3. 8 Hybrid Composition Functions (F12-F19): They are non-separable functions built by combining two functions belonging to the set of functions F1-F11.(Description) (Source code).

Complementary Material: SOCO Special Issue on Large Scale Continuous Optimization Problems

This section contains the following complementary material of the special issue:

M. Lozano, F. Herrera, D. Molina (Eds.). Scalability of Evolutionary Algorithms and other Metaheuristics for Large Scale Continuous Optimization Problems. Soft Computing, Volume 15, number 11, 2011.

NEWS: The special issue has been published. In the following, this page provides the articles, with the source code of the presented proposals and their results (in Excel format).

Introduction

Large scale continuous optimisation problems have been one of the most interesting trends in the last years for what concerns research on evolutionary algorithms and metaheuristics for continuous optimization problems, because they appear in many real-world problems (bio-computing, data mining, etc.). Unfortunately, the performance of most available optimisation algorithms deteriorates very quickly when the dimensionality increases. The reasons appear to be two-fold. First, complexity of the problem usually increases with the size of problem, and second, the solution space of the problem increases exponentially with the problem size, and a more efficient search strategy is required to explore all the promising regions in a given time budget. Thus, scalability for high-dimensional problems becomes an essential requirement for modern continuous optimisation algorithm approaches. Recent research activities have been organized to provide a forum to disseminate and discuss the way evolutionary algorithms and metaheuristics may respond to increase the dimensionality of continuous optimization problems.

This special issue is primarily intended to bring together the works of active researchers of this emerging field to present the latest developments. Its main motivation was to identify key mechanisms that may make evolutionary algorithms and metaheuristics to be scalable on those problems. An interesting added feature is that it accompanies with an associated Website where the source codes and results of the proposals are available to the specialized research community. In order do to do this, a set of scalable benchmark function optimization problems were considered as test suite and particular requirements on the simulation procedure were specified. All the authors executed their algorithms following these guidelines and provided the obtained results.

Experimental Framework

A set of 19 scalable function optimization problems were provided:

  • 6 Funcionts: F1-F6 of the CEC'2008 test suite. A detailled description may be found in: K. Tang, X. Yao, P. N. Suganthan, C. MacNish, Y. P. Chen, C. M. Chen, and Z. Yang. Benchmark Functions for the CEC'2008 Special Session and Competition on Large Scale Global Optimization. Technical Report, Nature Inspired Computation and Applications Laboratory, USTC, China, 2007. (Source code).
  • 5 Shifted Functions: Schwefel’s Problem 2.22 (F7), Schwefel’s Problem 1.2 (F8), Extended f10 (F9), Bohachevsky (F10), and Schaffer (F11). (Source code).
  • 8 Hybrid Composition Functions (F12-F19*): They are non-separable functions built by combining two functions belonging to the set of functions F1-F11 (Description) (Source code).

Document with a complete description of the 19 test functions: Description F1-F19*

  • Each algorithm is run 25 times for each test function.
  • The performance measures that were provided are:
    • Average of error of the best individuals found in the 25 runs. For a solution x, the error measure is defined as: f(x)-f(op), where op is the optimum of the function.
    • Maximum error achieved in the 25 runs.
    • Minimum error achieved in the 25 runs.
    • Median of the error achieved in the 25 runs.
  • The study was made with dimensions D = 50, D = 100, D=200, D=500, and D = 1,000. The maximum number of fitness evaluations is 5,000·D. Each run stops when the maximal number of evaluations is achieved.

Mainly, the authors were requested to make an analysis of the scalability behaviour of their proposed algorithms and a comparison (by applying non-parametric tests) against three baseline evolutionary algorithms for continuous optimization problems:

  • Real-coded CHC (Eshelman, L.J., Schaffer, J.D. (1993). Real-coded genetic algorithms and interval-schemata. In: Foundations of Genetic Algorithms 2, L. D. Whitley, Ed. San Mateo, CA: Morgan Kaufmann, p. 187–202).
  • G-CMA-ES (Auger, A., Hansen, N. (2005) . A restart CMA evolution strategy with increasing population size. In: Proc. of the 2005 IEEE Congress on Evolutionary Computation, p. 1769-1776).
  • Differential Evolution (Storn, R., Price, K. (1997). Differential evolution – a simple and efficient heuristic for global optimization over continuous spaces. Journal of Global Optimization 11 (4), 341–359).

Information for the baseline algorithms: (Components and Parameters of DE, Real-coded CHC, and G-CMA-ES) (Souce code) (Excel file)

Results of the Algorithms

The results (average error) of the algorithms listed below are available: Excel file

Table of Contents

Manuel Lozano; Daniel Molina; Francisco Herrera
Editorial scalability of evolutionary algorithms and other metaheuristics for large-scale continuous optimization problems
Soft Computing, 15, pages: 2085-2087, 2011.

P01 - Algorithm: SOUPDE
Matthieu Weber, Ferrante Neri, Ville Tirronen
Shuffle Or Update Parallel Differential Evolution for Large Scale Optimization
Soft Computing, 15, pages: 2089-2107, 2011.
Source code Excel file

P02 - Algorithm: DE-D^40+M^m
Carlos García-Martínez, Francisco J. Rodríguez, Manuel Lozano
Role Differentiation and Malleable Mating for Differential Evolution: An Analysis on Large Scale Optimisation
Soft Computing, 15, pages: 2109-2126, 2011.
Source code Excel file

P03 - Algorithm: GODE
Hui Wang, Zhijian Wu, Shahryar Rahnamayan
Enhanced Opposition-Based Differential Evolution for Solving High-Dimensional Continuous Optimization Problems
Soft Computing, 15, pages: 2127-2140, 2011.
Source code Excel file

P04 - Algorithm: GaDE
Zhenyu Yang, Ke Tang, Xin Yao
Scalability of Generalized Adaptive Differential Evolution for Large-Scale Continuous Optimization
Soft Computing, 15, pages: 2141-2155, 2011.
Source code Excel file

P05 - Algorithm: jDElscop
Janez Brest, Mirjam Sepesy Maucec
Self-adaptive Differential Evolution Algorithm using Population Size Reduction and Three Strategies
Soft Computing, 15, pages: 2157-2174, 2011.
Source code Excel file

P06 - Algorithm: SaDE-MMTS
S.Z. Zhao, P.N. Suganthan, S. Das
Self-adaptive Differential Evolution with Multi-trajectory Search for Large Scale Optimization
Soft Computing, 15, pages: 2175-2185, 2011.
Source code Excel file

P07 - Algorithm: MOS
A. LaTorre, S. Muelas, J.M. Peña
A MOS-based Dynamic Memetic Differential Evolution Algorithm for Continuous Optimization A Scalability Test
Soft Computing, 15, pages: 2187-2199, 2011.
Source code (Updated) Excel file
Note: The source code has been updated, fixing a problem in the numering of the functions.

P08 - Algorithm: MA-SSW-Chains
Daniel Molina, Manuel Lozano, Ana M. Sánchez, Francisco Herrera
Memetic Algorithms Based on Local Search Chains for Large Scale Continuous Optimisation Problems: MA-SSW-Chains
Soft Computing, 15, pages: 2201-2220, 2011.
Source code Excel file

P09 - Algorithm: RPSO-vm
José García-Nieto, Enrique Alba
Restart Particle Swarm Optimization with Velocity Modulation: A Scalability Test
Soft Computing, 15, pages: 2221-2232, 2011.
Source code Excel file

P10 - Algorithm: Tuned IPSOLS
Marco A. Montes de Oca, Dogan Aydin, Thomas Stützle
An Incremental Particle Swarm for Large-Scale Optimization Problems: An Example of Tuning-in-the-loop (Re)Design of Optimization Algorithms
Soft Computing, 15, pages: 2233-2255, 2011.
Source code Excel file

P11 - Algorithm: multi-scale PSO
Yamina Mohamed Ben Ali
Multi-Scale Particle Swarm Optimization Algorithm
Source code Excel file

P12 - Algorithm: EvoPROpt
Abraham Duarte, Rafael Martí, Francisco Gortazar
Path Relinking for Large Scale Global Optimization
Soft Computing, 15, pages: 2257-2273, 2011.
Source code Excel file

P13 - Algorithm: EM323
Vincent Gardeux, Rachid Chelouah, Patrick Siarry, Fred Glover
EM323 : A Line Search based algorithm for solving high-dimensional continuous non-linear optimization problems
Soft Computing, 15, pages: 2275-2285, 2011.
Source code Excel file

P14 - Algorithm: VXQR
Arnold Neumaier, Hannes Fendl, Harald Schilly, Thomas Leitner
VXQR: Derivative-free unconstrained optimization based on QR factorizations
Soft Computing, 15, pages: 2287-2298, 2011.
Source code Excel file

Software

Basic and Classic Algorithms

  • Real Evolutionary Algorithm (Realea) Library

This library is created to give a framework for real coding optimizations using optimization algorithms, like Evolutionary Algorithms (LS) and Local Search Methods. Its aim is to allow the researcher to focus only on the implementation of its algorithm. It includes the source code of test suites indicated in this page.

  • README.txt
  • Software (the official repository), inside it has a Doxygen documentation.
  • Genetic Algorithm (GA)
    This source code implements the Genetic Algorithm (GA) proposed by Goldberg, D.E., Genetic Algorithms in Search, Optimization, and Machine Learning. Kluwer Academic Publishers, Boston, MA.

 

 

  • Particle Swarm Optimization (PSO)

These source code implement the classic Particle Swarm Optimization (PSO) proposed by J. Kennedy and R.C. Eberhart in j. Kennedy and R.C. Eberhart. Particle Swarm Optimization. Proceeding of IEEE International Conference on Neural Networks, IV, pages 1942–1948, 1995.

 

  • Differential Evolution (DE)

This source code implements the classic Differential Evolution (DE) proposed by R. Storn and K. Price in Storn, R. and Price, K. Differential Evolution - A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces. Journal of Global Optimization, 11, pages 341-359, 1997.

In HomePage of Storn with Code they can be obtained source code in other languages (Matlab, Python, ...).

 

  • Scatter Search

This source code implements real-coding Scatter Search defined by M. Laguna and R. Martí in M. Laguna, R. Martí. Scatter Search: Methodology and Implementations in C. Kluwer Academic Publishers, Boston, 2003.

 

 

  • Central Force Optimization (CFO)
    This source code implements the Central Force Optimization (CFO) proposed by R.A. Formato in R.A. Formato, Central Force Optimization: A New Metaheuristic with Applications in Applied Electromagnetics. Progress In Electromagnetics Research 77, 2007, 425-491 doi: 10.2528/PIER07082403.

    Source Code (Windows Basic using Fortran) by Richard A. Formato (author of the algorithm).
    Send your questions to CFO_questions@yahoo.com.

 

Advanced Algorithms

 

  • Memetic Algorithm Based on Local Search Chains for Large Scale Global Optimization (MA-SW-Chains)
    This source code implements MA-CMA-Chains proposed in Molina, D. and Lozano, M. and Herrera, F. MA-SW-Chains: Memetic Algorithm Based on Local Search Chains for Large Scale Continuous Global Optimization, In proceeding of WCCI 2010 IEEE World Congress on Computational Intelligence, pages 3153-1160, 2010.

    Source Code (C++), by D. Molina dmolina@decsai.ugr.es.

 

  • Several advanced Differential Evolutions (DE, OBDE, SaDE, JADE, DEGL, SFSLDE)
    This source code implements several advances proposed in

    OBDE: S. Rahnamayan, H. Tizhoosh, M. Salama, Opposition-based differential evolution, IEEE Transaction on evolutionary computation, vol. 12, pp 64–79. 2008.

    SaDE: A. K. Qin, V. L. Huang, P. N. Suganthan, Differential evolution algorithm with strategy adaptation for global numerical optimization, IEEE Transactions on Evolutionary Computation, vol. 13, number 2, pp 398–417. 2009.

    JADE: J. Zhang, A. C. Sanderson, JADE: Adaptive differential evolution with optional external archive, IEEE Transactions on Evolutionary Computation, vol. 13, number 5, pp. 945–958. 2009.

    DEGL: S. Das, A. Abraham, U. K. Chakraborty, A. Konar, Differential evolution using a neighborhood-based mutation operator, IEEE Transactions on Evolutionary Computation, vol. 13, number 3, pp 526–553. 2009.

    SFSLDE: F. Neri, V. Tirronen, Scale factor local search in differential evolution, Memetic Computing, vol. 1, number 2, pp 153–171. 2009.

    Source code (Java) by Isaac Triguero triguero@decsai.ugr.es and Pablo David Gutiérrez pdgutipe@gmail.com (API in Spanish)

    Result obtained in the 25 functions of CEC'2005:

 

  • Several advanced Particle Swarm Optimization algorithms
    This source code implements several advances proposed in

    PSO: Basic particle swarm optimization with inertia weight. J. Kennedy, R. Eberhart Particle Swarm Optimization, IEEE International Conference on Neural Networks:1942-1948 (1995)

    Selection PSO: P. Angelinne, Using Selection to Improve Particle Swarm Optimization, IEEE icec:84-90 (1998)

    Constriction PSO: M. Clerc, J. Kennedy , The particle swarm-explosion, stability and convergence in a multidimensional complex space, IEEE Transations on Evolutinary Computation: 58-73 (2002)

    Stretching PSO: K.E. Parsopoulos, M.N. Vrahatis Recent approaches to global optimization problems through Particle Swarm Optimization Natural Computing 1 235-306 (2002)

    Composite PSO: K.E. Parsopoulos, M.N. Vrahatis Recent approaches to global optimization problems through Particle Swarm Optimization Natural Computing 1 235-306 (2002)

    Fully Informed PSO: R. Mendes, J. Kennedy, J. Neves, The Fully Informed Particle Swarm: Simpler, Maybe Better, IEEE Trans. Evol. Comput. vol 8:3 (2004)

    Hierarchical PSO: S. Janson, M. Middendorf, A Hierarchical Particle Swarm Optimizer and its adaptative Variant, IEEE Trasn. on Systems, Man, And Cybernetics Vol 35:6 1272-1282 (2005)

    Frankenstein PSO: M.A. Montes de Oca, T. Stützle, M. Birattari, M. Dorigo, Frankenstein's PSO: A Composite Particle Swarm Optimization Algorithm IEEE Trans. Evol. Comput. Vol 13:5 pp. 1120-1132 (2009)

    Orthogonal Learning PSO: Z-H Zhan, J. Zhang, Y. Li, Y-H. Shi, Orthogonal Learning Particle Swarm Optimization, IEEE Trans. Evol. Comput. Vol 15:6 pp. 832-847 (2011)

    Source code (Java) by Pablo David Gutiérrez pdgutipe@gmail.com (API in Spanish)

 

  • CMA Evolution Strategy (CMA-ES)
    This source code implements CMA-ES proposed in Hansen, N., S.D. Müller and P. Koumoutsakos (2003). Reducing the Time Complexity of the Derandomized Evolution Strategy with Covariance Matrix Adaptation (CMA-ES). Evolutionary Computation, 11(1), pp. 1-18, 2003.

    Source Code obtained from HomePage of N. Hansen

 

  • BI-Population CMA Evolution Strategy (BIPOP-CMAES)
    This source code implements BIPOP-CMAES, winner of the GECCO 2010 BBOB competition, proposed in Hansen, N. (2009). Benchmarking a BI-Population CMA-ES on the BBOB-2009 Function Testbed. Workshop Proceedings of the GECCO Genetic and Evolutionary Computation Conference, ACM, pp. 2389-2395 (abstract and pdf, erratum, bibtex).

    Source Code obtained from HomePage of N. Hansen

 

  • MA-MPC
    This source code implements MA-MPC that was proposed in Saber M. Elsayed; Ruhul A. Sarker; Daryl L. Essam. GA with a New Multi-Parent Crossover for Solving IEEE-CEC2011 Competition Problems, in Proc. Congress on Evolutionary Computation, pp. 1034 - 1040, New Orleans, June 2011. This algorithm is the winner of the Special Track: Competition: Testing Evolutionary Algorithms on Real-world Numerical Optimization Problems CEC'2011.

    Source Code (Matlab) by Saber M. Elsayed; Ruhul A. Sarker; Daryl L. Essam. Source Code obtained from HomePage of the Special Session by P.N. Suganthan

 

  • G3PCX
    This source code implements the G3PCX proposed by Deb, K., Anand, A., and Joshi, D. in K. Deb, A. Anand, and D. Joshi, A computationally efficient evolutionary algorithm for real-parameter optimization, Evolutionary Computation, vol. 10, no. 4, pp. 371–395, 2002.

    Source Code (C) by K. Deb and his students, obtained from HomePage of K. Deb

Slides

UNDER CONSTRUCTION

Test Functions and Results

25 Benchmark functions (CEC'2005). Dimensions: 10, 30, 50. Special Session on Real-Parameter Optimization. 2005 IEEE CEC, Edinburgh, UK, Sept 2-5. 2005. Organizers: K. Deb and P.N. Suganthan.

 

7 Benchmark functions (CEC'2008). Dimension 100, 500, and 1000. Special Session & Competition on Large Scale Global Optimization. 2008 IEEE CEC, Hong Kong, June 1-6, 2008. Organizers: Ke Tang, Xin Yao, P.N. Suganthan, and Cara MacNish.

 

19 Benchmark functions. Dimension 100, 200, 500, and 1000. Special Issue of Soft Computing. Guest Editors: Francisco Herrera, Manuel Lozano.

 

20 Benchmark functions (CEC'2010). Dimension 1000. Special Session on Large Scale Global Optimization. 2010 IEEE CEC, Barcelona, July 18-23, 2010. Organizers: Ke Tang, Xiaodong Li, and P. N. Suganthan.

 

14 Benchmark functions for Real Problems (CEC'2011). Different Dimensionality. Special Session on Testing Evolutionary Algorithms on Real-world Numerical Optimization Problems. 2011 IEEE CEC, New Orleans, Jun 5-8, 2011. Organizer: P. N. Suganthan.

Statistical test based methodologies for Algorithm Comparisons

The use of statistical tests for the experimental study is necessary to support the conclusions. Because the basic hypothesis of parametric tests usually are not verified, the use of non-parametric tests is recommended.

The following paper that compares some evolutionary algorithms presented at CEC'05 Special Session on Real Parameter Optimization as a case of study:

S. Garcia, D. Molina, M. Lozano, F. Herrera, A study on the use of non-parametric tests for analyzing the evolutionary algorithms' behaviour: a case study on the CEC'2005 Special Session on Real Parameter Optimization. Journal of Heuristics 15 (2009) 617-644. doi: 10.1007/s10732-008-9080-4. PDF Icon

General information and software on these tests may be found in the following website http://sci2s.ugr.es/sicidm/.

Future Events

Large Scale Global Optimization.
2013 IEEE Congress on Evolutionary Computation (CEC'2013) June 20-23, 2013, Cancún, Mexico. Organizers: Xiaodong Li, Ke Tang, Zhenyu Yang.

Website of the special sesion
Deadline March 15, 2013
Special Session & Competition on Real-Parameter Single Objective Optimization.
2013 IEEE Congress on Evolutionary Computation (CEC'2013) June 20-23, 2013, Cancún, Mexico. Organizers: J. J. Liang, B. Y. Qu, P. N. Suganthan.

Website of the special sesion
Deadline March 15, 2013