Randomized Greedy Multi-Start Algorithm for the Minimum Common Integer Partition Problem
M. Lozano, F. J. Rodriguez, D. Peralta, C. García-Martínez, Randomized Greedy Multi-Start Algorithm for the Minimum Common Integer Partition Problem.
Abstract
In this paper, we propose a randomized greedy multi-start algorithm for the minimum common integer partition problem. Given $k$ multisets $S_1, \ldots, S_k$ of positive integers ($S_i=\{s_{i1},\ldots,s_{ij},\ldots,s_{im_i}\}$), the goal is to find the common integer partition $T$ with minimal cardinality, i.e., a unique and reduced multiset $T$ that, for each $S_i$, it can be partitioned into $m_i$ multisets $T_j$ so that the elements in $T_j$ sum to $s_{ij}$.
This mathematical problem is reported to appear in computational molecular biology, when assigning orthologs on a genome scale or assembling DNA fingerprints in particular. Our proposed metaheuristic approach constitutes the construction of multiple solutions by a new greedy method that embeds a diversification agent to allow diverse and promising solutions to be reached. Furthermore, we formulate an integer programming model for this problem and show that the CPLEX solver can only solve small instances of the problem. However, computational results for problem instances involving up to 1000 multisets (each one with up to 1000 elements) show that our innovative metaheuristic produces very good feasible solutions in reasonable computing times, arising as a very attractive alternative to the existing approaches.
Experimental Comparison
Results
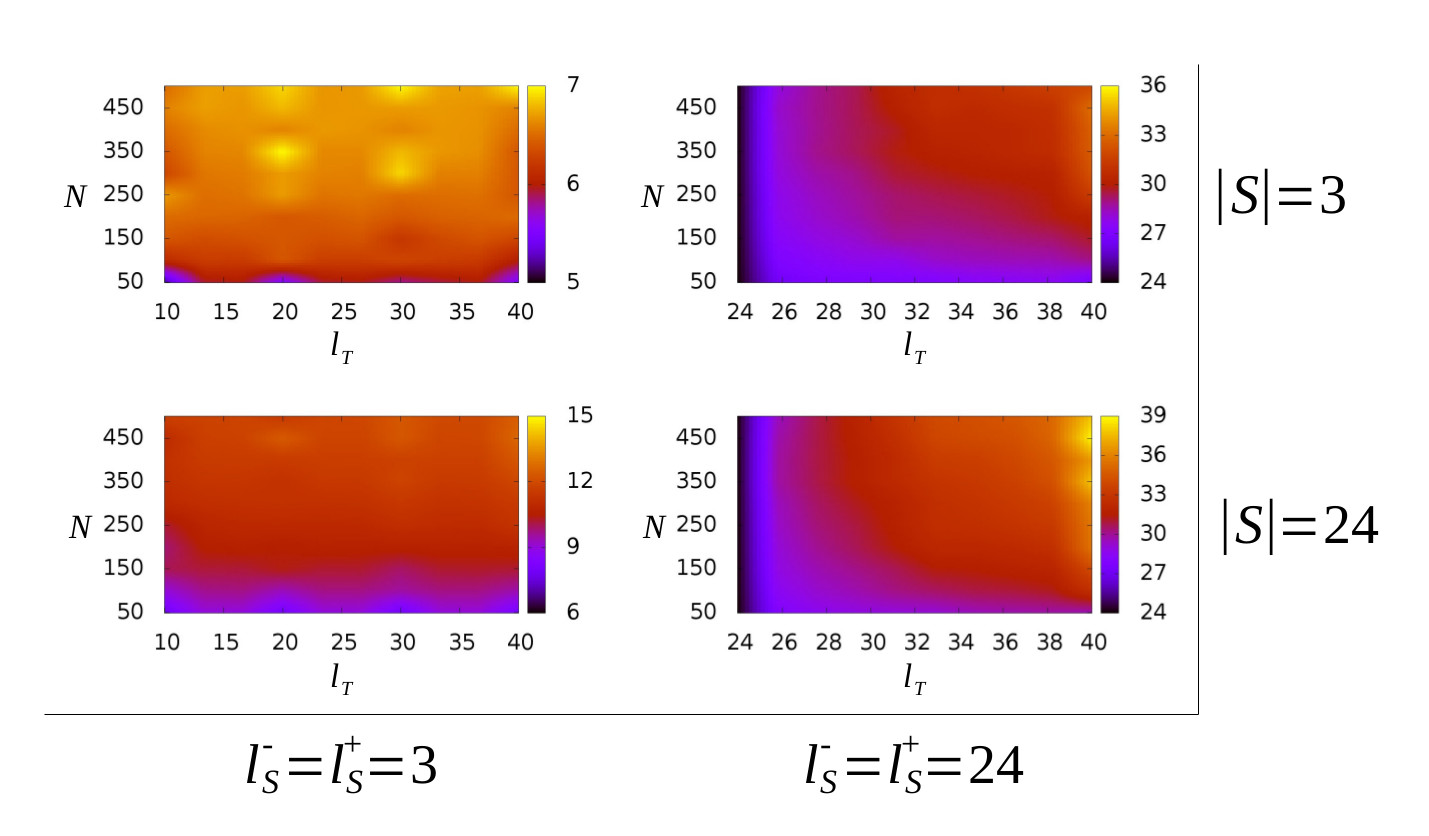
In the following figure, we show the averaged number of components of the solutions that our deterministic greedy produced over 10 random instances per combination of values for $l_T$, $k=|S|$, $N$, and $l^-_{S}=l^+_S$.
Instances for the MCIP problem
We provide a program, for Linux x64 systems, that implements the instance generator described in the paper. It takes five parameters: $l_T$, $k=|S|$, $N$, $l^-_{S}$, and $l^+_S$.
RGMS-MCIP: executable version
We provide an executable version of our algorithm for Linux x64 systems. It takes two parameters, the name of the file with the instance's data and the cut-off time in seconds.
