Integrating Instance Selection, Instance Weighting and Feature Weighting for Nearest Neighbor Classifiers by Co-evolutionary Algorithms - Complementary Material
This Website contains complementary material to the paper:
J. Derrac, I.Triguero, S. García and F.Herrera, Integrating Instance Selection, Instance Weighting and Feature Weighting for Nearest Neighbor Classifiers by Co-evolutionary Algorithms. IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics 42:5 (2012) 1383-1397, doi: 10.1109/TSMCB.2012.2191953 ![]()
The web is organized according to the following summary:
CIW-NN model
Co-evolutionary model
The CIW-NN model is composed by three populations, wich cooperates within a sequential co-evolutionary scheme. The first one performs a IS process (binary codification), guided by the CHC evolutionary model. The second one performs a FW process (real codification), employing a Steady-State genetic algorithm to conduct the search. This algorithm is also used by the last population, which performs a IW process.
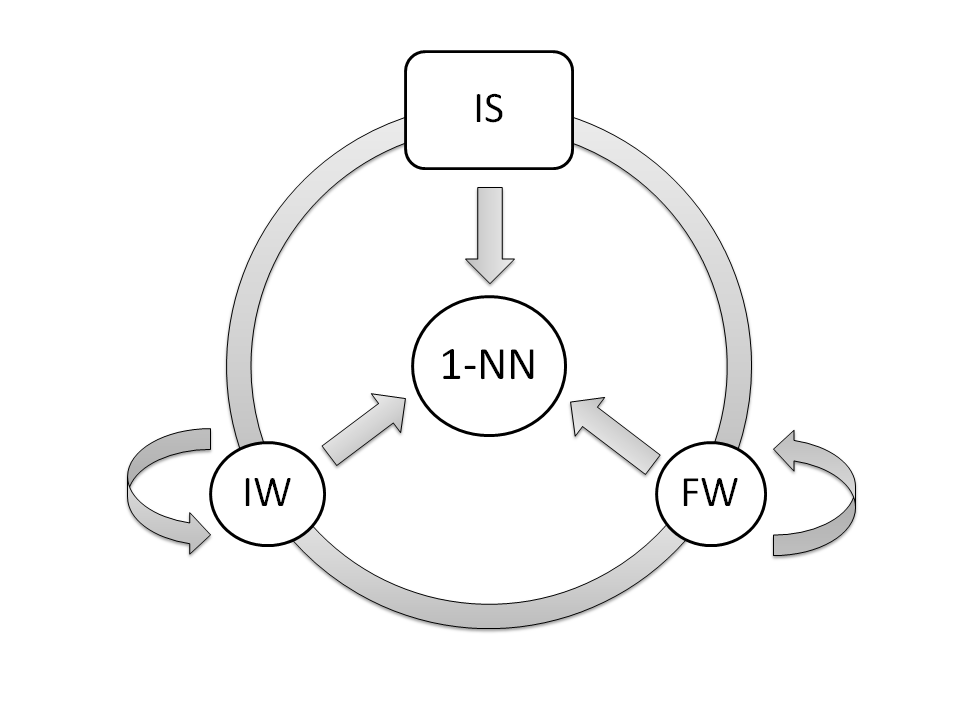
An epoch scheme is used to manage the populations. IS epochs only spend one generation, while FW and IW generations spend several. This scheme allows individuals of every population to cooperate properly through the fitness function of the model (a 1-NN classifier).
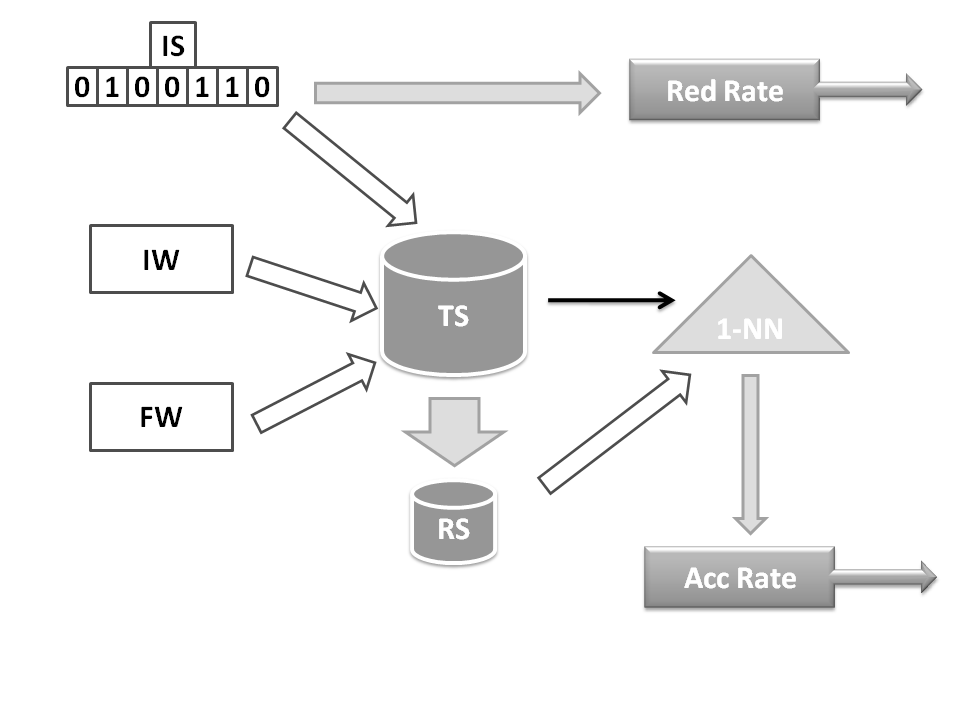
The fitness function needs one chromosome form each population. Reduction rates are computed directly by the subset of the training data selected by the IS chromosome. Accuracy rate is obtained by applying IS, FW and IW chromosomes over the training set, TS, to obtain the reference set RS. This reference set is employed by a 1-NN classifier to estimate the accuracy rate by means of a leave one out classification process of the entire training data.
Basic Evolutionary Search Techniques
The CIW-NN uses two different Evolutionary Algorithms to conduct the search: CHC and a Steady-State Genetic Algorithm with a crossover operator with multiple descendants.
CHC
CHC is a binary-coded GA which involves the combination of a selection strategy with a very high selective pressure, and several components inducing a strong diversity. Due to these characteristics, CHC has become a robust EA, which should offer promising results in several search problems.
The four main components of the algorithm are shown as follows:
- An elitist selection: The members of the current population are merged with the offspring population obtained from it and the best individuals are selected to compose the new population. In cases where a parent and an offspring have the same fitness value, the former is preferred to the latter.
- A highly disruptive crossover: The Half Uniform Crossover (HUX), which crosses over exactly half of the non-matching alleles, where the bits to be exchanged are chosen at random without replacement. This way, it guarantees that the two offspring are always at the maximum Hamming distance from their two parents, thus encouraging the introduction of high diversity in the new population and lessening the risk of premature convergence.
- An incest prevention mechanism: During the reproduction step, each member of the parent (current) population is randomly chosen without replacement and paired for mating. However, not all these couples are allowed to cross over. Before mating, the Hamming distance between the potential parents is calculated and if half this distance does not exceed a difference threshold d, they are not mated. d is initialized to L/4 (with L being the chromosome length). If no offspring is obtained in one generation, the difference threshold is decremented by one.
The effect of this mechanism is that only the more diverse potential parents are mated, but the diversity required by the difference threshold automatically decreases as the population naturally converges.
- A restart process: It replaces the GA mutation, is only applied when the population has stagnated. The difference threshold is considered to measure the stagnation of the search, which happens when it has dropped to zero and several generations have been run without introducing any new individual into the population. Then, the population is reinitialized by considering the best individual as the first chromosome of the new population and generating the remaining chromosomes by randomly flipping a 35 % of their bits.
Below is shown a basic pseudocode of CHC.

The main drawback of the application of CHC in the IS problem is that the efficiency of its fitness function depends on the phenotipe of the chromosome (If there are many 1's in the chromosome, many instances will be selected, increasing the cost of the 1-NN classification performed to compute its fitness value).
Therefore, in order to increase the speed of the data reduction process performed by the IS population, we have applied two modifications to the original algorithm:
- We have modified the definition of the HUX-cross operator. In this manner, when a gene representing an instance is going to be set from 0 to 1 by the crossing procedure, it is only set to 1 with a defined probability (prob0to1 parameter). No modifications are applied to changes from 1 to 0. For example, if one chromosome, 1100000000, and another chromosome, 1111111111, defining an IS classifier, are crossed by the HUX standard operator, the offspring may be 1111110000 and 1100001111. In the same scenario, a run of our HUX modified operator, with a probability of change prob0to1=0.5, would give as the output the offspring 1100110000 and 1100001111:

- The initialization of the individuals at the start of the algorithm is made randomly, but only a small fixed number of genes are set to 1. Therefore, in the initialization of a chromosome, each gene has a probability prob1 to be set to 1.
The prob0to1 parameter does not have a great impact on the results if it is kept in the interval (0.2-0.5). A value lower than 0.2 may bias the search, making it very difficult for CHC to preserve the quantity of 1's in the chromosomes. This may force the algorithm to produce solutions with high reduction rates but very low performance in accuracy due to the impossibility of selecting enough instances to represent the initial training set properly. On the other hand, a value higher than 0.5 will diminish the effect of the modified HUX-cross operator, thus producing solutions with lower reduction rates. Consequently, we have defined prob0to1= 0.25 as an optimal set up. The prob1 also does not have a great impact on the results, as long as it is set to a low value. Defining a value of 0.5 will be the same as defining just a random initialization. Thus, this value has to be lower. In our first experiments, we have found that prob1= 0.25 is an optimal set up for this value, which helps CHC to quickly obtain reduced solutions without biasing too much the search process due to a severe lack of 1's in the initial chromosomes.
Steady-State Genetic Algorithm with a crossover operator with multiple descendants
A SSGA is a GA where usually only one or two offspring are produced in each generation. Parents are selected to produce offspring and then a decision is made as to which individuals in the population will be selected for deletion in order to make room for the new offspring. Below is shown a pseudocode of a basic SSGA model.

Our concrete implementation of SSGA has the following features:
- Binary tournament is applied to select the parents (in order to select a parent, two individuals are randomly taken from the current population. Then, the one with the best fitness value is selected. This procedure is carried out twice to obtain the two parents requested).
- The offspring is obtained by applying a crossover process with multiple descendants. This process consists of repeatedly applying one or more standard crossover operators to obtain several new individuals (six or eight are common numbers). Then, the two best performing are selected as the new offspring.
From all the options suggested in (Sanchez et al, 2009), we have selected the Blend Crossover operator (BLX-α), applying it four times with values 0.3, 0.5, 0.5 and 0.7 for α (2BLX0.3-4BLX0.5-2BLX0.7). Below is shown a scheme of its application.
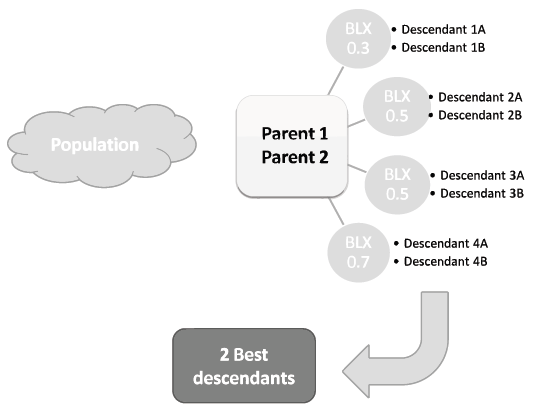
- A mutation operator is applied to every descendent obtained during the multiple descendent crossing process. We have used the non-uniform mutation operator. Mutation probability is set to a low value, 0.05 per chromosome, to avoid harming the convergence capabilities of the crossover operator.
- The two individuals of the current population with the worst fitness value are replaced by the new offspring.
